指導経験20年以上のプロ家庭教師。北海道の高校受験に特化。勉強がとても苦手な子の指導が得意です。
＞＞ブログ記事一覧（目次）
＞＞5教科・偏差値別オススメ問題集一覧
＞＞的中率60%以上！今年度の北海道公立高校入試「理科」はここが狙われる！家庭教師のそらの予想出題分野
■北海道公立高校入試のボーダー(合格)ライン・最低点の推移
＞＞北海道公立高校入試の道コン最低点推移のランク別まとめ
■北海道の公立高校の最終倍率推移
＞＞北海道の公立高校の最終倍率推移
■北海道公立高校入試の平均点推移と予想
＞＞北海道公立高校入試の平均点推移・各科目の正答率・人数分布・平均点予想まとめ
■北海道公立高校一般入試の合否判定の手順
＞＞【最新版】北海道公立高校一般入試の合否判定の手順の詳細まとめ
講評：過去5年間で最も易しいセット
2022年の北海道公立高校入試「理科」は、昨年度から大幅に易化しています。
2022年は制度変更1年目ということで、難化すると予想しましたが、実際には過去5年間で最も易しいセットでした。
ちなみに過去5年間の難易度は、
2020年 ≒ 2018年＞＞2019年＞＞2021年＞＞2022年
です。
いつもですと、時間内に解答不能な問題が混ざっていました。
例：
制度変更では、「思考力を試す」問題が出ると、教育委員会が公表していました。
が、実際にはすべての問題が典型問題で、問題集を完璧にしておけば、満点が取れるセットでした。
2020年の方が、思考力（国語力）が要求される試験ですね。2020年は解説を作るのが、本当に大変でした。
今回の入試より、総合ABCの方が明らかに難しいので、こちらは注意しておきましょう。
大問1 小問集合
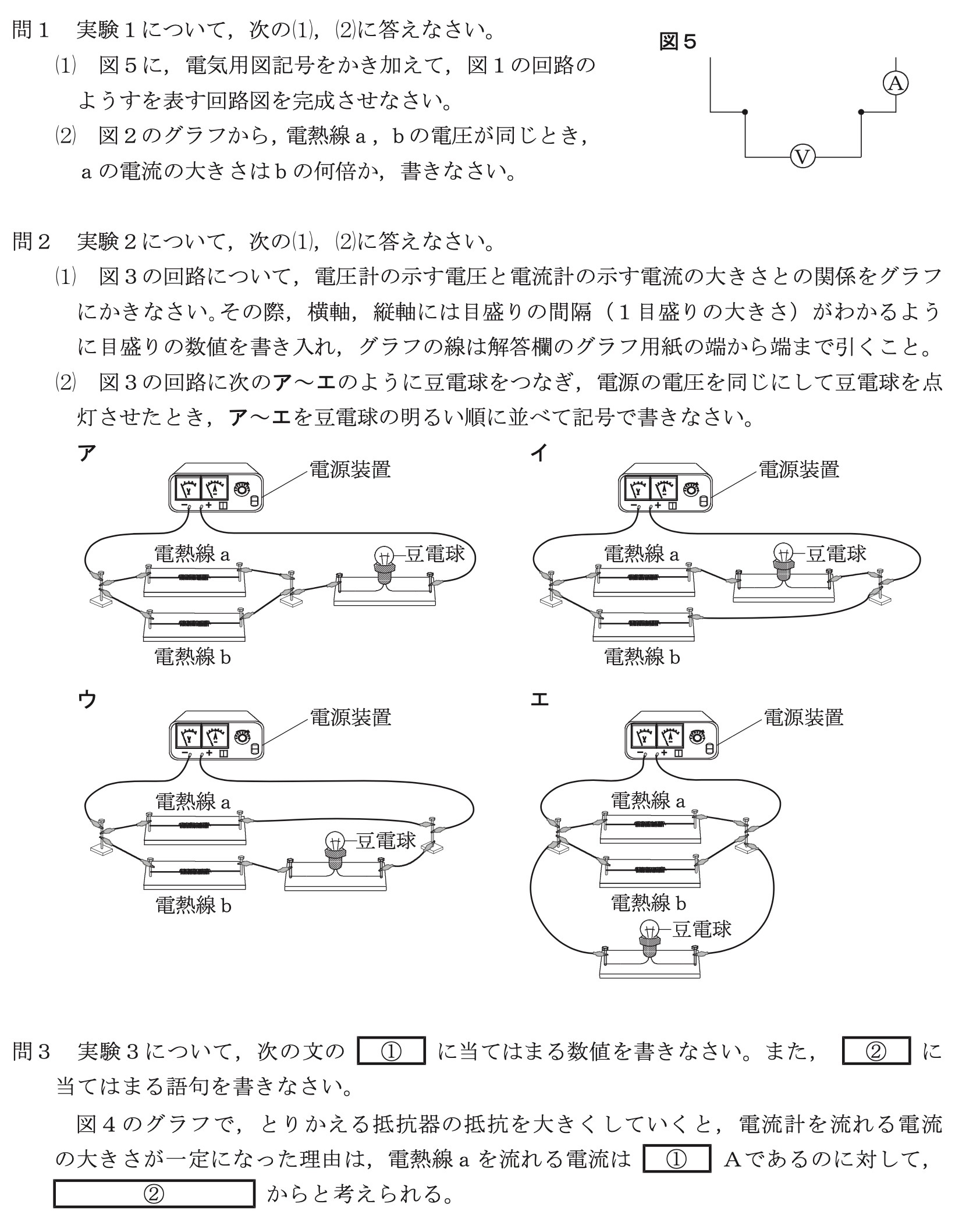
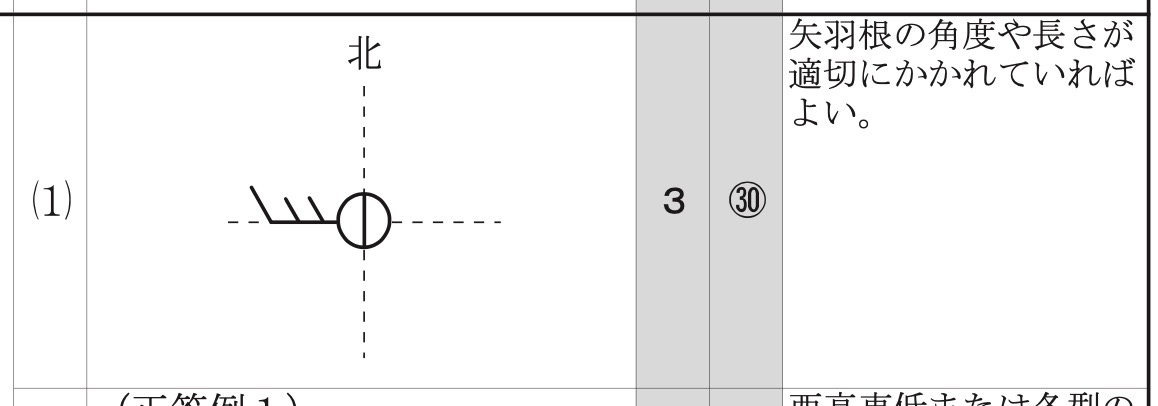
問1（1）
解答：屈折
解説：
単なる知識問題なので、略。
問1（2）
解答：光沢
解説：
同上。
問1（3）
解答：染色体
解説：
同上。
問1（4）
解答：黒点
解説：
同上。
問1（5）
解答：音源
解説：
同上。
問1（6）
解答：沸点
解説：
同上。
問1（7）
解答：分離
解説：
同上。
問1（8）
解答：惑星
解説：
同上。
問2
解答：42（cm/s）
解説：
求める単位は「cm/s」＝「距離（cm）÷秒（s）」です。
1秒が50打点より、5打点は0.1秒に相当します。
この運動では、0.1秒間で合計4.2cm移動しているので、平均の速さは、
4.2cm/0.1s＝42cm/s
問3
解答：①電子 ②イ
解説：
例えば電池で銅とマグネシウムを用いると、イオン化傾向が大きいマグネシウムが溶けて電子を2個放出して、マグネシウムイオン（Mg2+）になります。
問4
解答：記号 B、名称 がく
解説：
花の4要素は、外側から、がく→花弁→おしべ→めしべ、の順です。
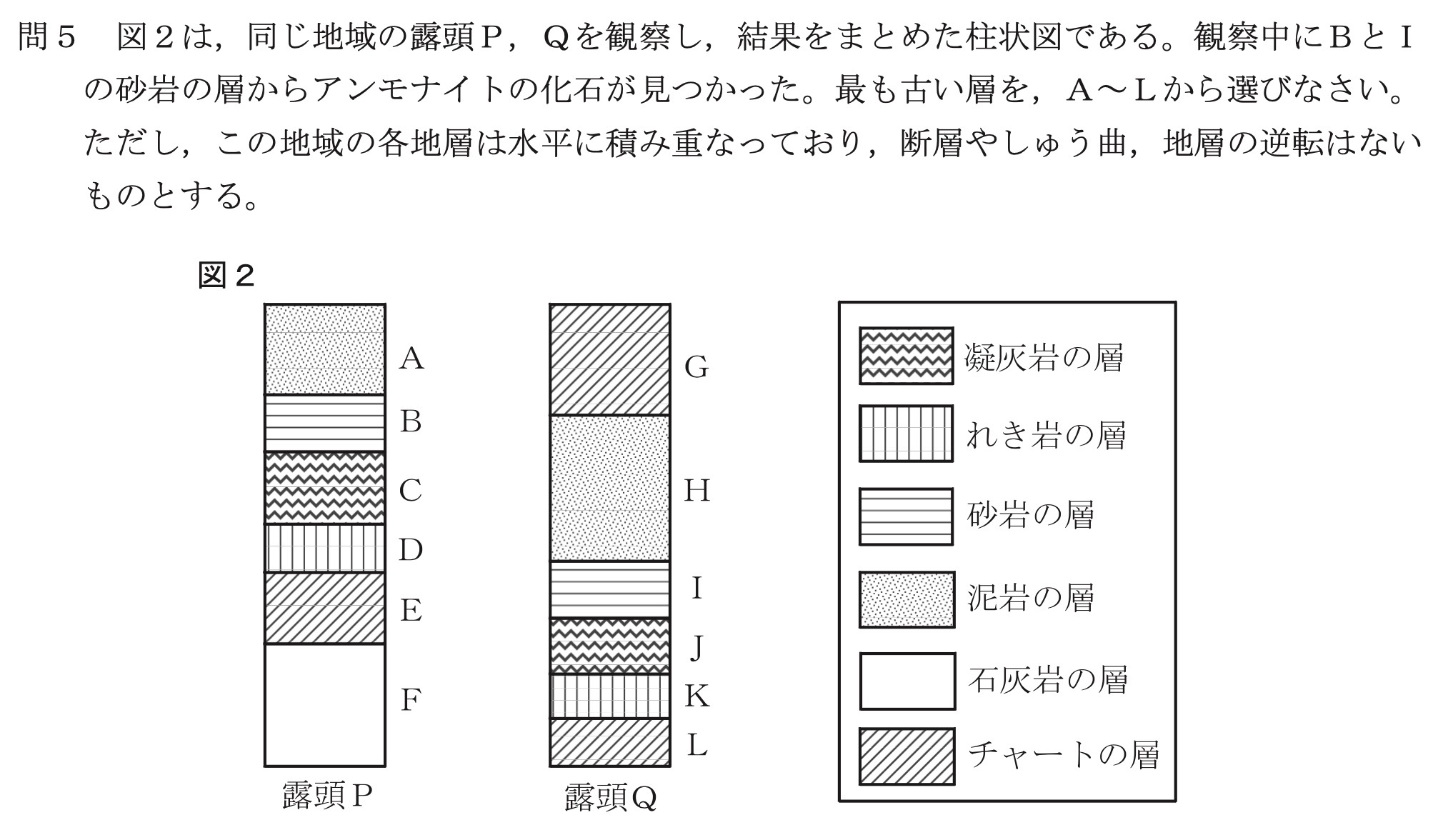
問5
解答：F
解説：
条件から、地層累重の法則により、最も古い地層は地層F（石灰岩の層）、最も新しい地層は地層G（チャートの層）です。
大問2 植物の茎の構造と蒸散量の計算＜生物＞
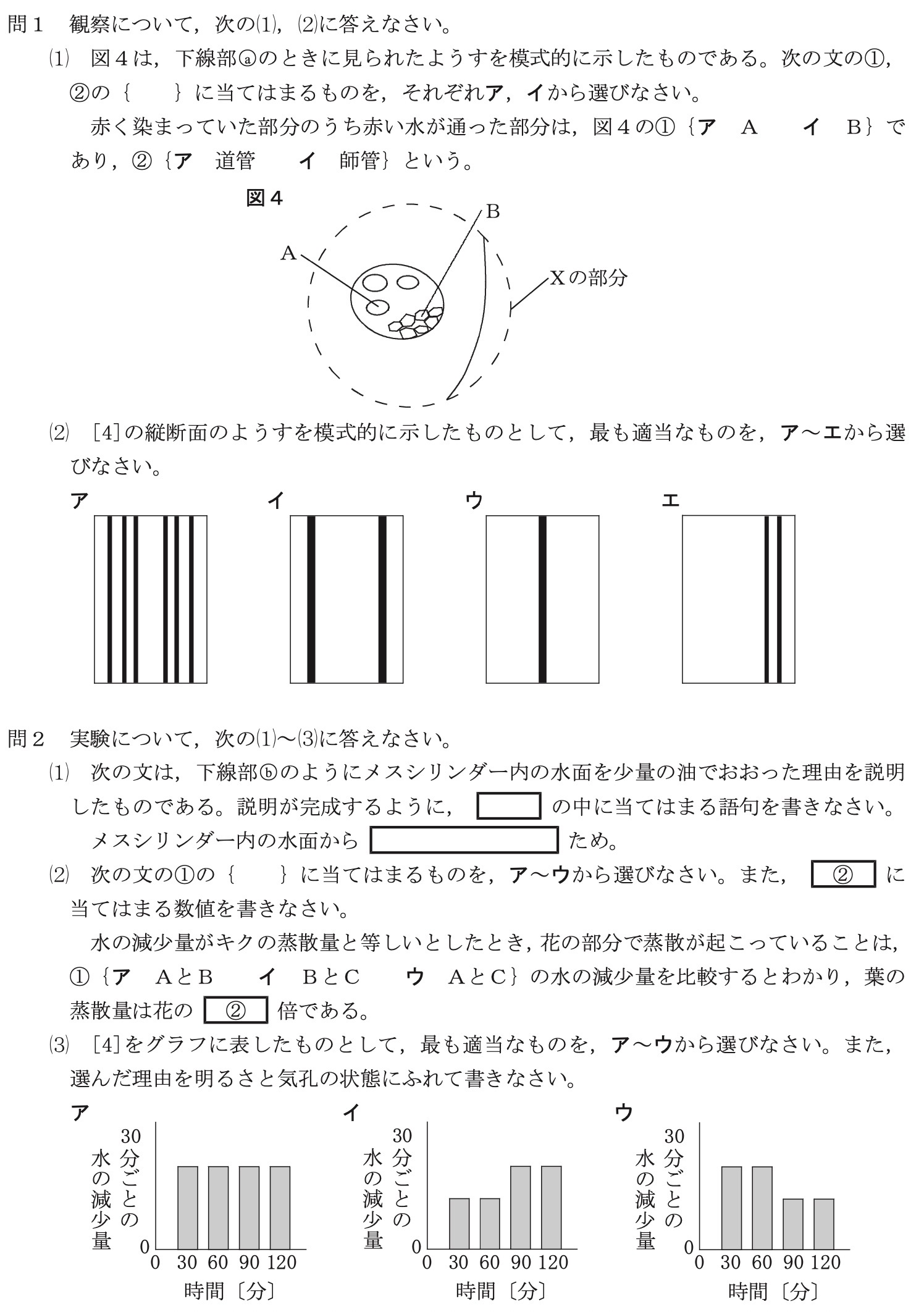
問1（1）
解答：①ア、②ア
解説：
Xの部分には、茎の維管束が含まれています。
茎の維管束は外側が師管（B）、内側が道管（A）です。
道管（A）は、水や肥料分が通る管なので、「図4」のうち赤い水が通るのは道管（①：ア、②：ア）です。
問1（2）
解答：イ
解説：
図2より、キクは双子葉類なので、断面図は選択肢イです。
図1より、アスパラガスは単子葉類なので、断面図は選択肢アです。
問2（1）
解答：（正答例）水が蒸発するのを防ぐ
解説：
単なる知識問題なので、略。
問2（2）
解答：①ウ、②3.8
解説：
「実験」の「表」から、蒸散が起こる場所を調べます。
キクA：葉＋茎（2.2cm3/3h）
キクB：茎（0.3cm3/3h）
キクC：花＋葉＋茎（2.7cm3/3h）
これより、花の蒸散量は、キクAとキクCを比較すればよいです（①：ウ）。
葉の蒸散量＝キクA（葉＋茎）- キクB（茎）＝2.2cm3/3h – 0.3cm3/3h = 1.9cm3/3h
花の蒸散量＝キクC（花＋葉＋茎） – キクA（葉＋茎）＝2.7cm3/3h – 2.2cm3/3h = 0.5cm3/3h
から、葉の蒸散量は花の蒸散量の、（1.9cm3/3h）÷（0.5cm3/3h）＝19/5＝3.8倍
問2（3）
解答： グラフ→イ、理由→（正答例）明るいところでは気孔が開くから。
解説：
単なる知識問題なので、略。
大問3 うすい塩酸と塩化銅水溶液の電気分解＜化学＞
★家庭教師のそらの予想は「ダニエル電池」でしたので、分野が的中しました！
問1（1）
解答：①水素、②イ
解説：
塩化水素の電離式は、
HCl → H+ ＋ Cl–
+と-は引き合うので、水素イオン（H+）は陰極（電極A）（②：イ）へ行き、電子を受け取りH同士が結合して水素（①）になります。
問1（2）
解答：①イ、②（正答例）水に溶けやすい
解説：
塩化物イオン（Cl–）より、塩素（Cl2）は陽極である電極Bで発生します。
塩酸の電気分解の化学反応式は、
2HCl → H2 ＋ Cl2
H2とCl2の係数の比が1：1より、H2がCl2同体積発生することになります。
しかし、陽極である電極Bで発生した塩素（Cl2）は水に溶けやすい性質（②）があるため、実際には塩素（Cl2）の方が集まる気体の量が少なくなります（①：イ）。
問2（1）
解答：Cu
解説：
塩化銅の電離式は、
CuCl2 → Cu2+ ＋ 2Cl–
これより、陽極である電極Dで塩素（Cl2）が、陰極である電極Cで銅（Cu）が発生します。
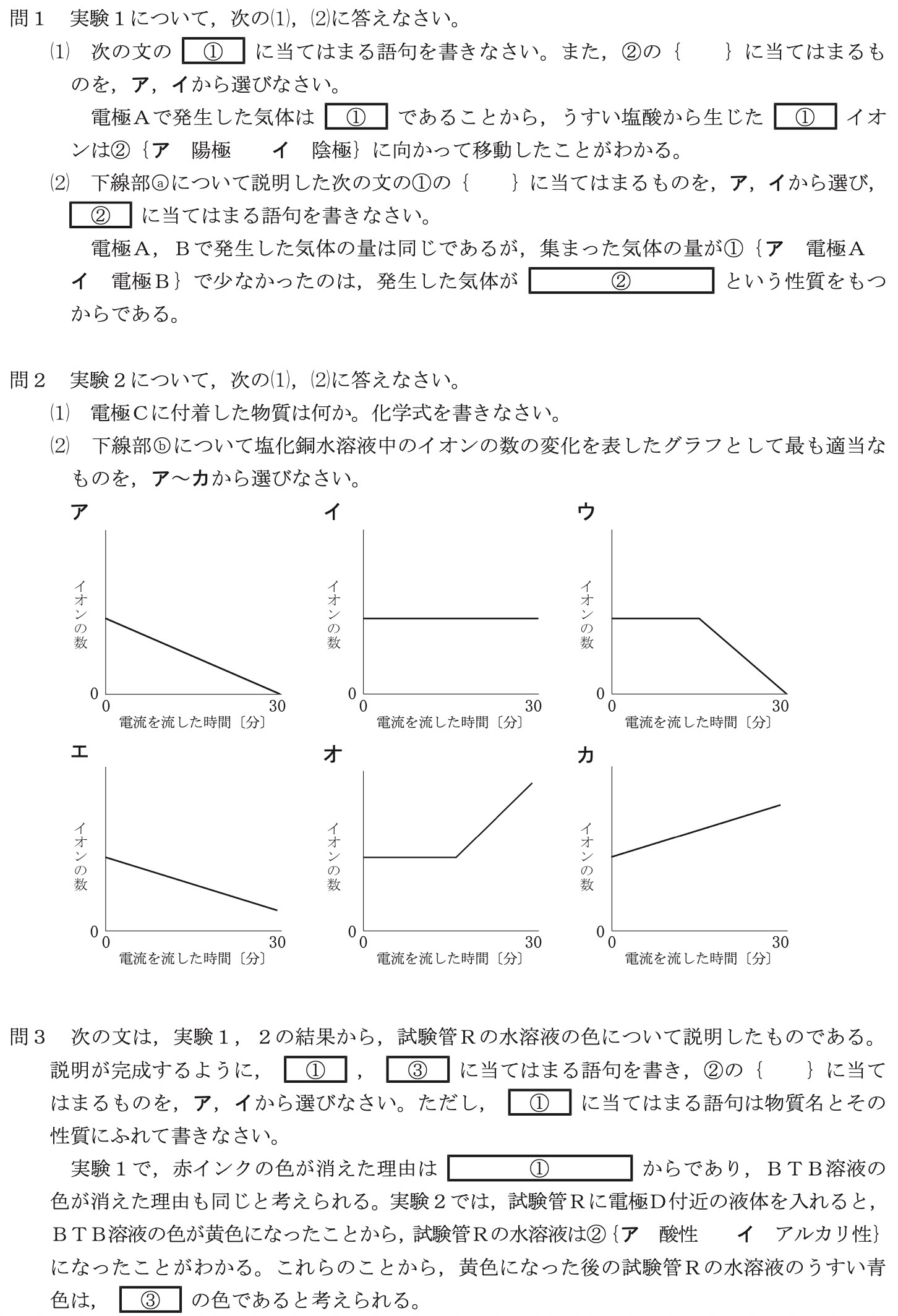
問2（2）
解答：エ
解説：
塩化銅の電気分解のメカニズムを、詳しく見ます。
CuCl2 → Cu2+ ＋ 2Cl–
・陽極（電極D）
Cl– → Cl ＋ e–
Cl ＋ Cl → Cl2
塩化物イオン（Cl–）が単位時間あたり2個ずつ減少していく＝直線の関係
・陰極（電極C）
Cu2+ ＋2e– → Cu
銅イオン（Cu2+）単位時間あたり1個ずつ減少していく＝直線の関係
これより、単位時間あたりにイオンが3個ずつ減少していく＝直線の関係になります。
実験2[4]には、「水溶液の色は実験前に比べ、うすくなった」とあり、無色になっていないので、青色の元である銅イオン（Cu2+）は水溶液にまだ残っています。
よって、答えは選択肢エです。
問3 ★やや難
解答：①（正答例）塩素に漂白作用がある、②ア、③（正答例）塩化銅水溶液
解説：
実験1[5]の試験管Pは、陽極である電極Bの液なので、塩素が溶けています。塩素には漂白作用があるため、赤インクの色が消えます。
BTB溶液がある試験管Qでは、黄色になったことから、陽極である電極Bの液は酸性です。黄色→無色になったのは、塩素の漂白作用のためです（①）。
実験1[5]から、塩素の漂白作用により、BTB液の黄色が脱色されることが分かります。
実験2[3]の試験管Rは、陽極である電極Dの液なので、塩素が溶けています。
BTB溶液の色が黄色になったことから、試験管Rの水溶液は酸性です（②）。
実験1[5]の結果から、塩素の漂白作用により、BTB液の黄色が脱色されます。
黄色→青色になったのは、BTB液の黄色が脱色され、元々あった青色の元である銅イオン（Cu2+）の色が現れたためです。この銅イオンは、塩化銅水溶液に含まれているので、青色は塩化銅水溶液の色と言えます（③）。
この実験より、塩素の漂白作用ではこの青色は脱色できないことが分かります。
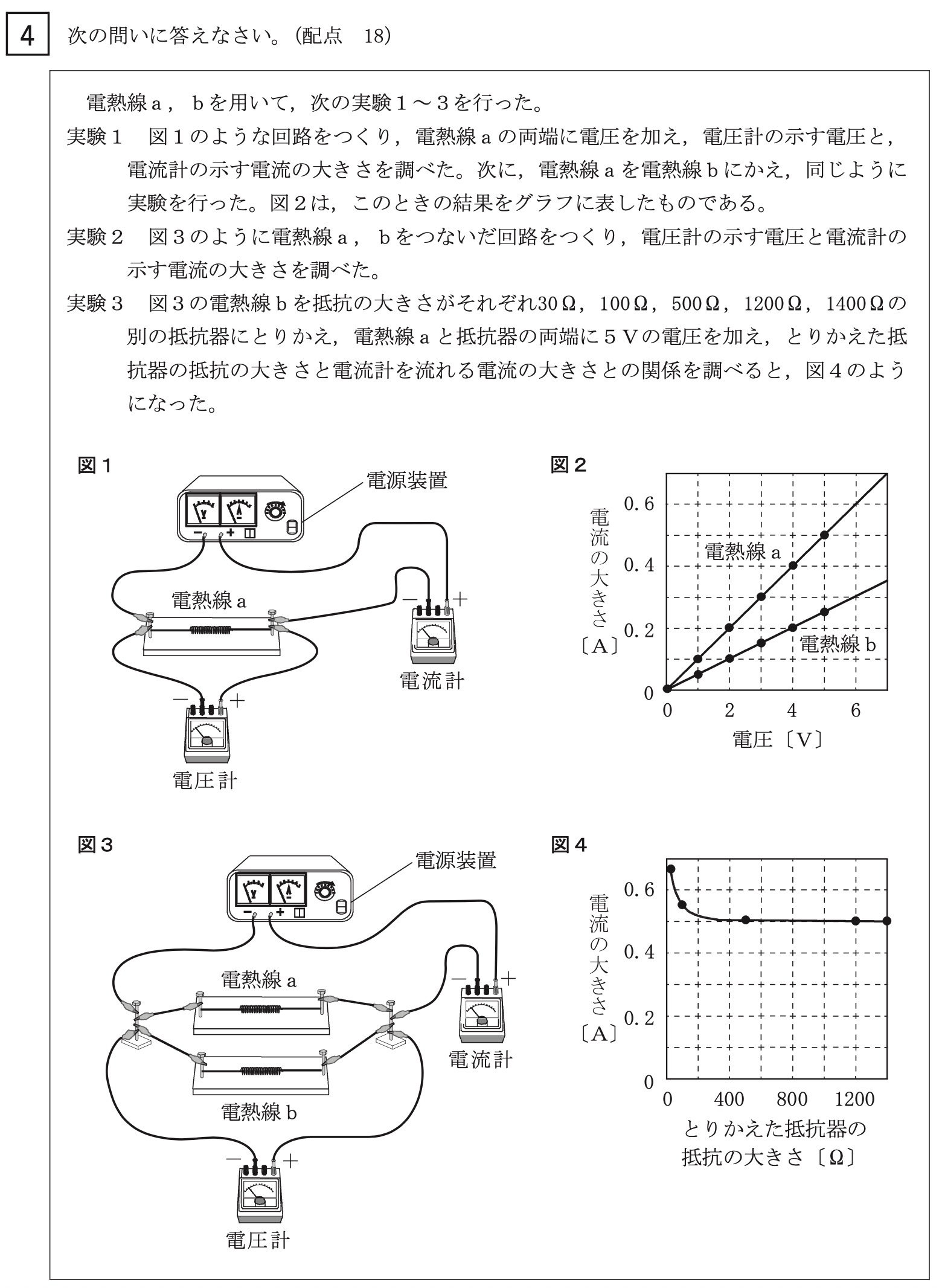
大問4 直列回路と並列回路の電流の大きさと豆電球の明るさ＜物理＞
★家庭教師のそらの予想は「発熱量の計算」でしたので、分野が的中しました！
問1（1）
解答：
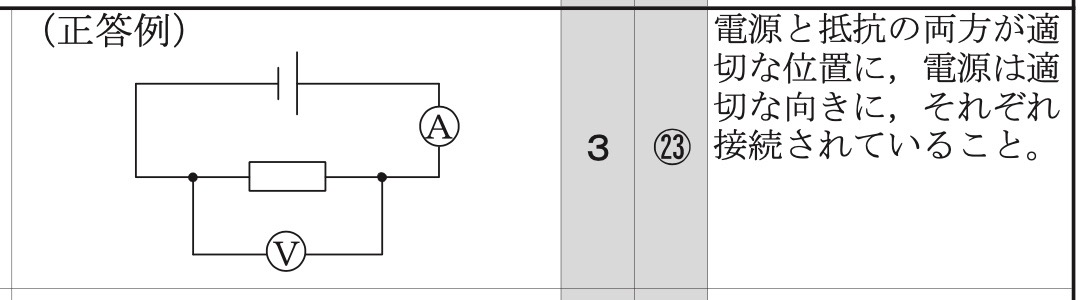
解説：
電流計は抵抗に直列に、電圧計は抵抗に並列に接続します。
問1（2）
解答：2（倍）
解説：
問題文に「図2のグラフから」とあるので、図2のグラフのみで判断します。
例えば4Vのとき、電熱線aでは0.4A、電熱線bでは0.2Aの電流が流れています。
これより、電熱線aの電流の大きさは、電熱線bの2倍（0.4A/0.2A）です。
問2（1） ★やや難
解答：
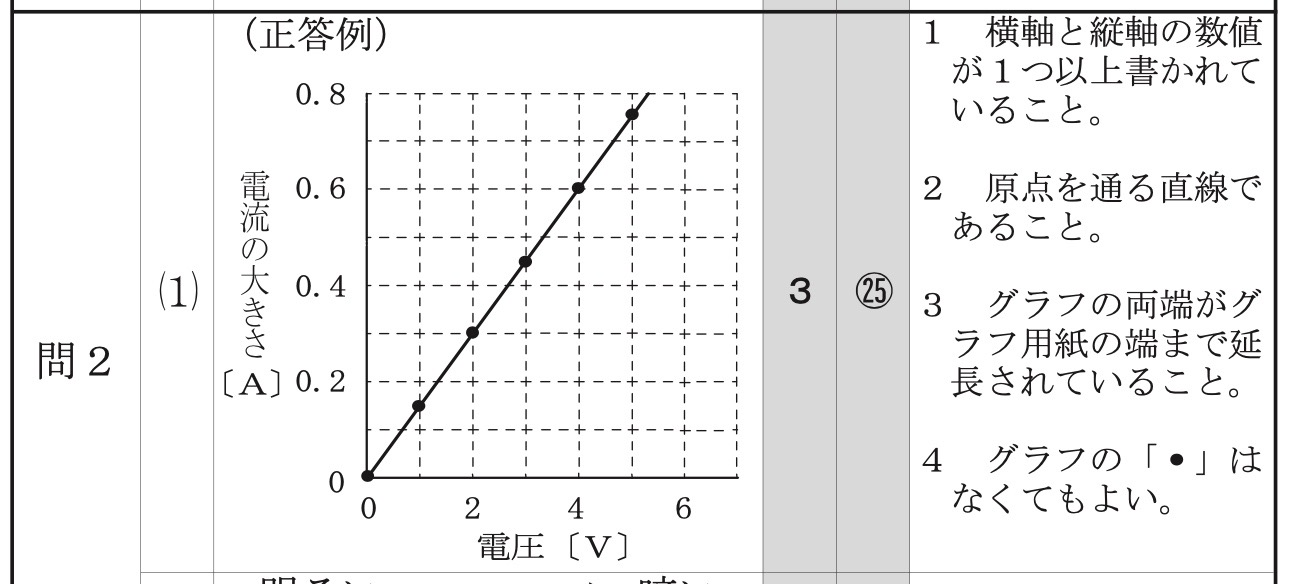
解説：
図2より、電熱線aの抵抗の大きさは、オームの法則から、
R＝4V/0.4A＝10Ω
電熱線bの抵抗の大きさは、同様にして、
R＝4V/0.2A＝40/2＝20Ω
図3は並列回路なので、回路全体の抵抗の大きさは、
R＝（10Ω×20Ω）÷（10Ω＋20Ω）＝20/3Ω
解答のグラフは縦軸が電流の大きさ、横軸が電圧の大きさなので、オームの法則を用いて、
V＝I×20/3Ω ⇔ I=3/20V
これより、（電圧(V)、電流(I)）＝（0、0）、（2V、0.3A）、（4V、0.6A）、（6V、0.8A）
の4点を結んで直線にするとよいでしょう。
問2（2） ★やや難だが良問
解答：（明るい→暗い）エ→ア→イ→ウ
解説：
消費電力の大きさが大きいほど、豆電球は明るくなります。
選択肢では、同じ電源装置を用いている、つまり電流の大きさが同じであるので、
消費電力 P[W] ＝ I[A]×V[V]＝I2R
の式を用います。
豆電球の抵抗の大きさが与えられていないので、適当に10Ωで統一します。消費電力の式より、豆電球を流れる電流の大きさを比較すればよいことが分かります。
電源装置の電圧の大きさも与えられていないので、適当に10Vとします。
・ア
（解1）
電熱線aと電熱線bと豆電球の合成抵抗＝10Ω×20Ω/（10Ω+20Ω）＋10Ω＝20/3＋30/3＝50/3Ω
電源装置を流れる電流の大きさ＝10V÷(50/3Ω)＝3/5A
豆電球を流れる電流の大きさ＝3/5A＝0.6A
（解2）
電熱線aと電熱線bの合成抵抗＝10Ω×20Ω/（10Ω+20Ω）＝20/3Ω
電熱線aと電熱線bの合成抵抗：豆電球の抵抗＝20/3Ω：10Ω＝20：30＝2：3より、
豆電球に加わる電圧の大きさ＝10V×3/5＝6V
豆電球を流れる電流の大きさ＝6V÷10Ω＝0.6A
・イ
（解1）
電熱線aと豆電球に加わる電圧の大きさ＝10V
電熱線aの抵抗：豆電球の抵抗＝10Ω：10Ω＝1：1より、
豆電球に加わる電圧の大きさ＝10V/2＝5V
豆電球を流れる電流の大きさ＝5V÷10Ω＝0.5A
（解2）
電熱線bを流れる電流の大きさ＝10V/20Ω＝0.5A
電熱線aと豆電球の抵抗：電熱線bの抵抗＝10Ω+10Ω：20Ω＝1：1より、
豆電球を流れる電流の大きさ＝0.5A
・ウ
（解1）
電熱線bと豆電球に加わる電圧の大きさ＝10V
電熱線bの抵抗：豆電球の抵抗＝20Ω：10Ω＝2：1より、
豆電球に加わる電圧の大きさ＝10V×1/3＝10/3V
豆電球を流れる電流の大きさ＝10/3V÷10Ω＝1/3A≒0.33A
（解2）
電熱線aを流れる電流の大きさ＝10V/10Ω＝1A
電熱線aの抵抗：電熱線bと豆電球の抵抗＝10Ω：10Ω＋20Ω＝1：3より、
豆電球を流れる電流の大きさ＝1A×1/3≒0.33A
・エ
豆電球を流れる電流の大きさ＝10V/10Ω＝1A
よって、電流の大きさが、エ(1A)＞ア(0.6A)＞イ(0.5A)＞ウ(0.33A)なので、明るさもこの順になります。
問3
解答：①0.5、②（正答例）抵抗器を流れる電流がほとんどなくなった
解説：
図2と図4より、電熱線aを流れる電流の大きさはオームの法則より、
V＝IR ⇔ I＝V/R＝5V/10Ω＝0.5A（①）
電熱線bの抵抗値が30Ω、100Ω、500Ω、1200Ω、1400Ωのとき、電熱線bを流れる電流の大きさは、
30Ωのとき、I＝V/R＝5V/30Ω＝1/6A≒0.17A＝170mA
100Ωのとき、I＝V/R＝5V/100Ω＝0.05A＝50mA
500Ωのとき、I＝V/R＝5V/500Ω＝1/100＝0.01A＝10mA
1200Ωのとき、I＝V/R＝5V/1200Ω＝1/240A＝1/240×1000mA≒4mA
1400Ωのとき、I＝V/R＝5V/1400Ω＝1/280A＝1/280×1000mA≒3mA
このように、電熱線bの抵抗値が大きくなると、電熱線b（抵抗器）を流れる電流の大きさがほとんどなくなることが分かります（②）。
大問5 冬の天気の特徴と湿度の計算＜地学＞
★家庭教師のそらの予想は「台風」でしたので、分野が的中しました！
問1（1）
解答：①等圧線、②ア
解説：
①は単なる知識問題なので、略。
冬は西高東低の気圧配置となり、図2よりオホーツク海上での等圧線の間隔が狭いので、風が強く吹き込みます。
問1（2）
解答：（正答例）小さく密度が大きくなる
解説：
温度が高いと空気に含まれる粒子の運動エネルギーが増して、空気が膨張して体積[cm3]が大きくなり、密度[g/cm3]が小さくなるため、空気が軽くなり上昇します。
空気が上昇すると地表付近の空気に含まれる粒子の数が減るため、質量[g]が減る＝重さ[N]が減るため、気圧（圧力[N/m2]）が減少し、低気圧となります。
温度が低いと空気に含まれる粒子の運動エネルギーが減少して、空気が収縮して体積[cm3]が小さくなり、密度[g/cm3]が大きくなるため、空気が重くなり下降します。
空気が下降すると地表付近の空気に含まれる粒子の数が増えるため、質量[g]が増える＝重さ[N]が増えるため、気圧（圧力[N/m2]）が増加し、高気圧となります。
問2（1）
解答：
解説：
単なる知識問題なので、略。
問2（2）
解答：
（正答例１）西高東低の気圧配置により、湿った空気が山脈で雪を降らせ、乾燥して太平洋側にふき下るため。
（正答例2）北西の季節風が、山脈で雪を降らせて、太平洋側に流れるため。
解説：
冬は大陸側が冷たく（高気圧）、日本の太平洋側が暖かくなる（低気圧）ため、西高東低の気圧配置となります。
風は高気圧（冷たい）→低気圧（暖かい）の方向に吹くので、冬は北西の季節風になります。
大陸側で発達した高気圧がシベリア気団です。大陸にあるので、乾燥しています。
北西の季節風によって日本海で熱と水蒸気を補給して湿った空気となり、日本に上陸して山脈を上ると、空気の温度が下がって飽和水蒸気量以下になると、日本海側に雪を降らせ、水分を失い乾燥した空気になり、太平洋側に吹き降ります。
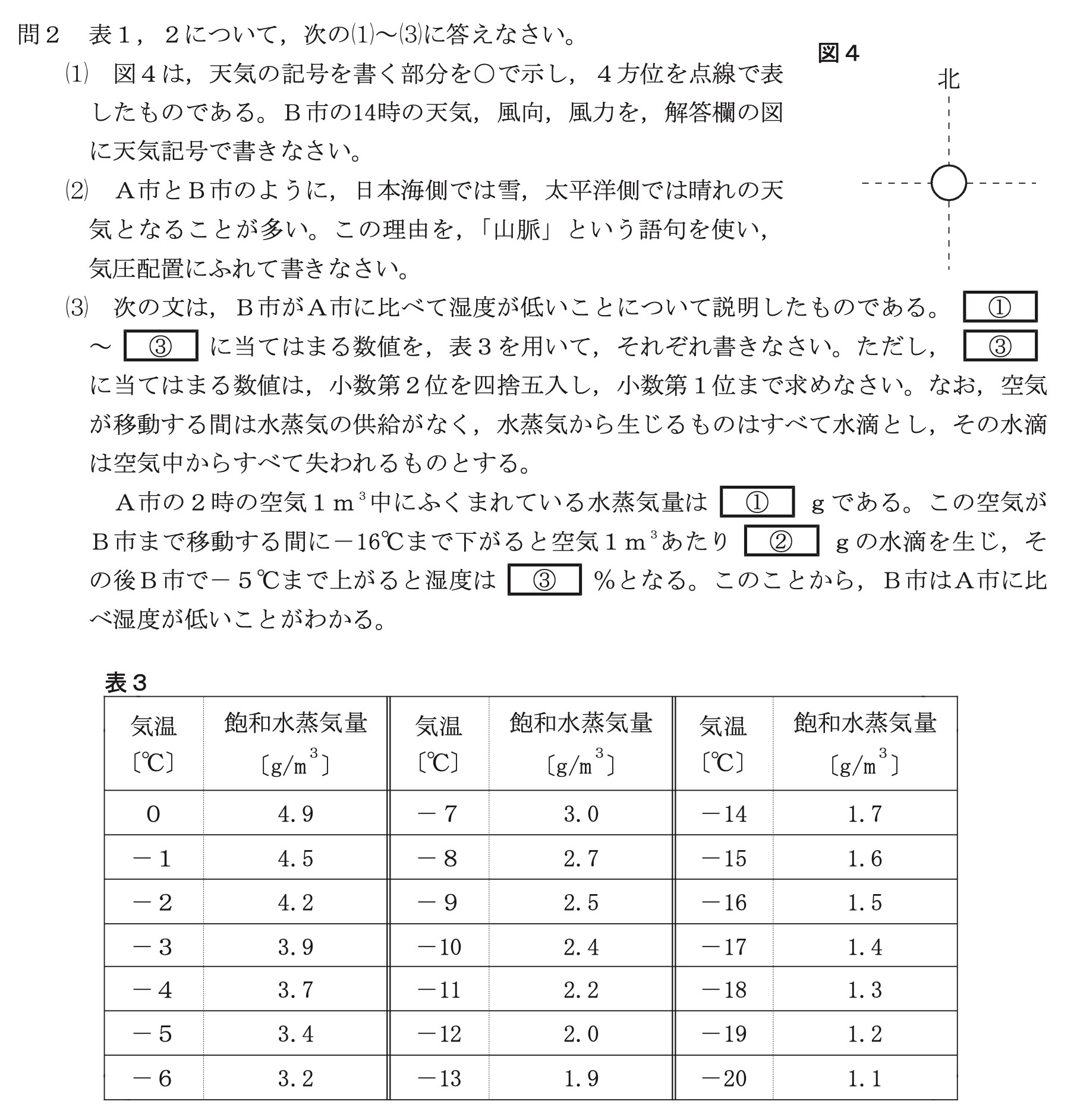
問2（3）
解答：①2.7、②1.2、③44.1
解説：
①
A市の2時の気温は表1より、-7℃です。-7℃のときの飽和水蒸気量は表3より、3.0g/m3です。A市の湿度は表1より90％なので、水蒸気量は、
3.0g/m3×0.9＝2.7g/m3
②
-16℃のときの飽和水蒸気量は表3より、1.5g/m3です。-7℃のときのA市の空気が含む水蒸気量は2.7g/m3なので、
2.7g/m3 – 1.5g/m3＝1.2g/m3
の水滴が生じます。
B市の空気が含む水蒸気量は飽和水蒸気量である1.5g/m3で、湿度は100％です。
③
-5℃のときの飽和水蒸気量は表3より、3.4g/m3です。
B市の空気が含む水蒸気量は1.5g/m3なので、湿度は
（1.5g/m3/3.4g/m3）×100＝1500/34＝750/17≒44.11･･･≒44.1％