こんにちは、個別指導塾まさです。
今回は、2021年11月10日(水)に行われた、中学3年北海道学力テスト総合C「理科」の問題・解答・詳しい解説を公開致します。
総合ABCの「範囲表」（最新版）は、こちらです。
〜〜〜総合ABCの過去問と解説はこちら〜〜〜
＞＞2022年総合Cの「理科」の問題・解答・詳しい解説 ★難しい★
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
今後の北海道公立高校入試の日程（最新版）は、こちらです。
＞＞【2024(令和6年)受験用】北海道公立高校入試はいつ何時から？日程・時間割・試験時間・持ち物などまとめ
＞＞的中率60%以上！今年度の北海道公立高校入試「理科」はここが狙われる！個別指導塾まさの予想出題分野
＞＞【最新版】北海道の公立・私立高校受験対策おすすめ問題集（道コンSS・高校別）と差がつく正しい使い方
オンライン個別指導塾と家庭教師をやっています。北大院卒、指導経験20年以上。当塾は中上位高校志望の子が多いですが、勉強が苦手な子も多数在籍しています。今の学力は不問ですので、気軽にお申し込みください。授業料は1回70分 3,000円〜です。
＞＞教師紹介・料金・授業内容
＞＞体験授業かんたんお申し込み
＞＞お問い合わせ
中学3年北海道学力テスト総合C「理科」(2021年)の難易度
2021年の総合C「理科」の難易度は、過去の総合ABCの中では最高レベルの難易度でした。
難易度の高い問題が至る所にあり、学力が高い子でも、解くのに苦労したはずです。
これまでの総合ABCの理科は定期テストより易しかったのですが、2020年を境に難しくなりました。
2021年はさらに難しくなり、今回の総合Cは11月の時点でこのレベルの問題を出すのはちょっと酷では、と思えるほどです。
2022年の入試は、2021年が易しかったこと、新入試に変わることから、難しかった2020年と2018年のレベルの問題が出題されると思っておいてください。
今回の最高レベルの難易度だった総合Cは、2020年と2018年の入試より易しいです。
北海道公立高校入試「理科」で高得点を狙うなら、この総合Cレベルの問題を、本番までに確実にできるようになりましょう。
対策として、まずは、標準レベル問題集『教科書ワーク』や『中学 理科 標準問題集』を仕上げることです。
そして、入試のゴールである 『塾技 理科80』を完全にして終わりです。
今回の最高レベルの難易度だった総合Cも、 『塾技 理科80』を完全にしていたら、満点近く取れます。
スポンサーリンク
中学3年北海道学力テスト総合C「理科」(2021年)の平均点・道コン偏差値SS
＜総合C「理科」の平均点と道コン偏差値(2021年)＞
44点
※道コンSS50に相当
中上位公立高校を受験するなら、第5回・6回の道コンは必ず受けましょう。
＞＞★的中率75％★道コン中3第5回・6回の理科の信憑性は高い！高校入試で的中した証拠【画像】
中学3年北海道学力テスト総合C「理科」(2021年)問題・解答・解説
大問1 混合物の蒸留（易〜標準レベル）
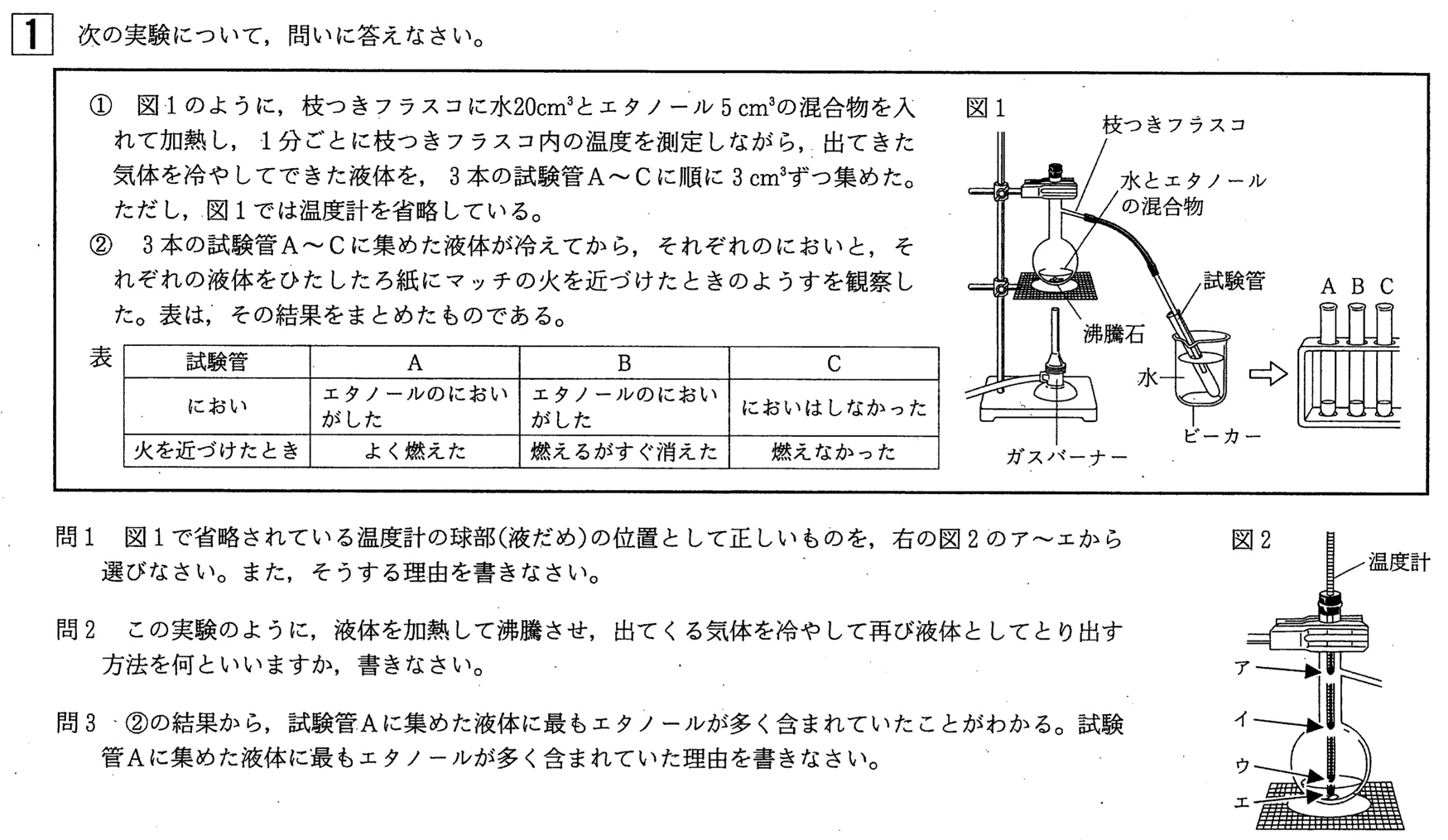
問1
解答：球部の位置･･･ア、理由･･･（枝つきフラスコから）出てくる蒸気（気体）の温度を測るため。
解説：
蒸留の実験では、蒸気の温度を測定するために、枝つきフラスコのうち、蒸気がガラス管へ流れる部分であるアの位置に温度計を設置します。
問2
解答：蒸留
解説：
略。
問3
解答：水よりも沸点が低いエタノールを多く含む気体が先に出てきたから（例）
解説：
純粋なエタノールの沸点は78.3℃、純水の沸点は100℃より、水とエタノールの混合物を加熱すると、最初は多量のエタノール＋少量の水（A）が捕集されます。
捕集された液体にはエタノールが多く含まれるため、火を近づけると燃えます。
この時の蒸気の温度は、エタノールの沸点付近になり、加熱を続けると蒸気の温度が水の沸点付近になり、少量のエタノール＋多量の水（C）が捕集されます。
捕集された液体には水が多く含まれるため、火を近づけても燃えません。
スポンサーリンク
大問2 銅とマグネシウムの酸化（難）
問1
解答：金属の粉末と酸素が触れる面積を大きくするため。（例）
解説：
中学理科の範囲での代表的な金属の酸化は、銅の酸化とマグネシウムの酸化です。
表1を得る実験は、図より銅の酸化です。
銅の酸化の実験では、加熱中しながら銅の粉末をよくかき混ぜて空気に十分に触れさせます。
下線部は「ステンレス皿にできるだけ薄く広げ」とあり、かき混ぜていないので、「金属（銅）の粉末を空気に十分に触れさせるため」と答えるとよいでしょう。
問2 ★やや難
解答：加熱後の物質の質量･･･エ、結びついた酸素の質量･･･ウ
解説：
公立高校入試によく出題されそうな問題です。本番までに出来るようになってください。
表1の＜金属X＞は、以下のように分解できます。
A（①）＝金属Xの粉末の質量
B（②）＝金属Xの粉末の質量＋ステンレス皿の質量
C（③）＝金属Xの粉末の質量＋ステンレス皿の質量＋金属Xの粉末と結びついた酸素の質量
・加熱後の物質の質量
加熱後の物質の質量＝金属Xの粉末の質量＋金属Xの粉末と結びついた酸素の質量
であるので、
C（③）（金属Xの粉末の質量＋ステンレス皿の質量＋金属Xの粉末と結びついた酸素の質量）-B（②）（金属Xの粉末の質量＋ステンレス皿の質量）+A（①）（金属Xの粉末の質量）＝C-（B-A）（エ）
と導くことができます。
・結びついた酸素の質量
これまでの考察により、
結びついた酸素の質量＝C（③）（金属Xの粉末の質量＋ステンレス皿の質量＋金属Xの粉末と結びついた酸素の質量）-B（②）（金属Xの粉末の質量＋ステンレス皿の質量）＝C-B（ウ）
と導くことができます。
問3 ★やや難
解答：金属･･･Y、酸素･･･ア
解説：
公立高校入試によく出題されそうな問題です。本番までに出来るようになってください。
問題文に「一定の質量の金属と結びつく」とあります。
実験の③に「粉末をガスバーナーで十分に加熱した」とあるので、金属の粉末が酸素と完全に反応したと考えることができます。
つまり、表1と表2から導ける「結びついた酸素の質量」は、一定の質量の金属と化合する酸素の質量であり、定比例の法則が成り立つと言えます。
表1と表2の2列目の数値を用いて、一定の質量と結びつく酸素の質量と、金属1.00gあたりに結びつく酸素の質量を計算します。
・金属X
問2の考察より、
一定の質量と結びつく酸素の質量＝C（③）-B（②）
であるので、
金属Xと結びつく酸素の質量＝9.00g-8.60g＝0.40g
・金属Y
金属Yと結びつく酸素の質量＝8.75g-8.60g＝0.15g＞金属Xと結びつく酸素の質量
よって、一定の質量の金属と結びつく酸素の質量が少ないのは、金属Yです。
反応前の金属Yの質量が0.60gのとき、金属Yと結びつく酸素の質量が0.15gより、
金属Yと結びつく酸素の質量[g]÷反応前の金属Yの質量[g]＝0.15g÷0.60g＝0.25g
上式の単位を含めて考えると、0.25g[金属Yと結びつく酸素の質量/反応前の金属Yの質量[g]であるので、反応前の金属Y1.00g当たりに結びつく酸素の質量が0.25gと読むことができます。
＜別解＞
表1より、「金属X：化合した酸素：酸化物」の質量比は、0.60g：0.40g：1.00g＝3：2：5＝12：8：20、です。
表2より、「金属Y：化合した酸素：酸化物」の質量比は、0.60g：0.15g：0.75g＝4：1：5＝12：3：15、です。
これより、
一定の質量の金属と結びつく酸素の質量が少ないのは、金属Yだと分かります。
また、
金属Xと結びつく酸素の質量[g]÷反応前の金属Xの質量[g]＝2÷3≒0.67g
金属Yと結びつく酸素の質量[g]÷反応前の金属Yの質量[g]＝1÷4＝0.25g
と求められます。
問4 ★難
解答：金属X：金属Y＝3：8
解説：
『塾技 理科80』に普通に書かれている内容ですが、難問です。公立高校入試では、もう少し易しい問題が出題されるはずです。
問3の考察より、金属Xの酸化反応は、マグネシウムの酸化（燃焼）です。マグネシウムの酸化の化学反応式は以下のとおりです。
2Mg + O2 → 2MgO
「マグネシウム(Mg)：化合した酸素（O2）：酸化物（MgO）」の質量比は、0.60g：0.40g：1.00g＝3：2：5、です。
化学反応式の左辺をみると、マグネシウム原子（Mg）と酸素原子（O）の個数の比が2：2より、同数あります。
酸素原子（O）2個＝酸素分子（O2）であるので、
マグネシウム(Mg)：化合した酸素（O2）＝マグネシウム原子(Mg)2個：化合した酸素原子（O）2個＝3：2
つまり、マグネシウム原子(Mg)1個：化合した酸素原子（O）1個＝3：2
という質量比が成り立ちます。
金属Yの酸化反応は、銅の酸化です。銅の酸化の化学反応式は以下のとおりです。
2Cu + O2 → 2CuO
「銅(Cu)：化合した酸素（O2）：酸化物（CuO）」の質量比は、0.60g：0.15g：0.75g＝4：1：5、です。
化学反応式の左辺をみると、銅原子（Cu）と酸素原子（O）の個数の比が2：2より、同数あります。
酸素原子（O）2個＝酸素分子（O2）であるので、
銅(Cu)：化合した酸素（O2）＝銅原子(Cu)2個：化合した酸素原子（O）2個＝4：1
つまり、銅原子(Cu)1個：化合した酸素原子（O）1個＝4：1
という質量比が成り立ちます。
まとめると、
マグネシウム原子(Mg)1個：化合した酸素原子（O）1個＝3：2
銅原子(Cu)1個：化合した酸素原子（O）1個＝4：1＝8：2
より、
銅原子(Cu)1個：マグネシウム原子(Mg)1個：化合した酸素原子（O）1個＝8：3：2
となるので、
酸素原子1個あたりと結びつく銅原子(Cu)とマグネシウム原子(Mg)の質量比は8：3です。
金属Xはマグネシウム(Mg)、金属Yは銅(Cu)であるので、答えは、
金属X(Mg)：金属Y(Cu)＝3：8
となります。
大問3 消費電力と発熱量（やや難）
問1
解答：12W
解説：
P[W]＝I[A]×V[V]＝I2R＝V2/R
与えられている情報が、6Vと3Ωなので、
P[W]＝V2/R＝36/3＝12W
問2
解答：1440J
解説：
P[W]＝P[J/s]です。
Q[J]＝P[J/s]×t[s]＝IVt＝I2Rt＝V2t/R
与えられている情報が、6Vと6Ωと4min=240sなので、
Q[J]＝V2t/R＝36×240/6＝6×240＝1440J
問3 ★やや難
解答：水が得た熱量･･･1260J、熱がある理由･･･発生した熱が器具の温度を下げたり、空気中に逃げたりするため。（例）
解説：
水が得た熱量[J]＝4.2g/℃×水の質量[g]×上昇温度[℃]
より、
電熱線Bの熱により水が得た熱量は、
4.2g/℃×100g×（3℃ – 0℃）＝420×3＝1240J
電熱線Bの熱エネルギーが全て水へ移ったとき、水が得た熱量＝電熱線Bの発熱量＝1440J、となります。
水が得た熱量(1240J)＜電熱線Bの発熱量(1440J)
となるのは、解答のとおりです。
なお、公立高校入試対策として、変換効率も抑えておきましょう。
電熱線Bから発生した熱エネルギー1440Jのうち、水が得た熱エネルギーは1240Jなので、
変換効率＝（水が得た熱エネルギー[J]/電熱線Bから発生した熱エネルギー[J]）×100＝（1240/1440）×100≒86.1％
となります。
問4 ★やや難
解答：Q（直）＜Q（B）＜Q（A）＜Q（並）
解説：
『塾技 理科80』より易しいですが、難問です。
しかし公立高校入試では、このレベルの問題は解けて欲しいところです。
Q[J]＝P[J/s]×t[s]＝IVt＝I2Rt＝V2t/R
電圧[V]と時間[s]は一定なので、発熱量Q[J]は抵抗[Ω]の値によって変化すると考えることができます。
Q[J]＝V2t/R
上式より、発熱量は抵抗に反比例します。
問題文の各通りについて、回路全体の抵抗（合成抵抗）の値を調べると、
電熱線A＝3Ω、電熱線B＝6Ω、電熱線AとBを直列に接続＝3Ω+6Ω＝9Ω、電熱線AとBを並列に接続＝(3Ω×6Ω)/(3Ω+6Ω)＝18/9＝2Ω
電熱線AとBを並列に接続＜電熱線A＜電熱線B＜電熱線AとBを直列に接続
であるので発熱量はこの逆になり、
Q（直）＜Q（B）＜Q（A）＜Q（並）
です。
大問4 浮力（易〜標準レベル）
問1
解答：
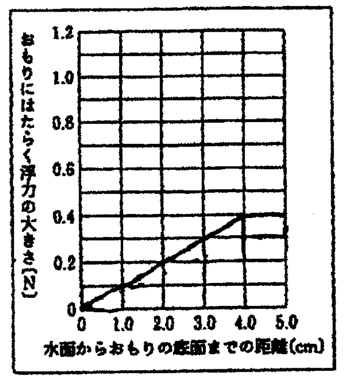
解説：
鉛直上向きの力と鉛直下向きの力がつり合うことで物体は静止するので、
ばねばかりの値[N]＋浮力[N]＝おもりに働く重力[N]
⇔ 浮力[N]＝おもりに働く重力[N] – ばねばかりの値[N]
おもりの質量＝120g、重力＝1N/100gより、おもりに働く重力＝1N/100g×120g＝1.2Nなので、
浮力[N]＝1.2N – ばねばかりの値[N]
あとは、グラフのばねばかりの値を用いて、浮力のグラフを書くことができます。
問2
解答：重力･･･1.2N、浮力･･･0.4N
解説：
重力の大きさは場所によらず一定であるので、問1より1.2Nです。
アルキメデスの原理より、浮力は物体が押しのけた水の重さに相当します。
水面からおもりの底面までの距離が6.0cmのとき、高さ5cmであるおもりは水中に完全に沈んでいるので、グラフより、ばねばかりの値は0.8Nです。
よって、
浮力[N]＝1.2N – ばねばかりの値[N]＝1.2N – 0.8N＝0.4N
です。
問3
解答：イ
解説：
水圧は水深に比例し、1cmあたり100Pa＝1hPaずつ増加していきます。
深いほど水圧は大きいので、選択肢イが正解です。
大問5 斜面とばねを用いた力のつり合い（やや難）
問1
解答：2.7J
解説：
このばねのばね定数は1N/cmであるので、ばねがおもりを引き上げる力の大きさは、4.5cm×1N/cm＝4.5Nです。
おもりを引き上げる間のばねの伸びは一定であったことから、ばねがおもりを引き上げる力の大きさは一定で、おもりが等速直線運動をしながら引き上げられたことが分かります。
よって仕事の大きさは、
仕事[J]＝おもりに加えた力[N]×おもりを移動させた距離[m]＝4.5N×0.6m＝4.5×6/10＝27/10＝2.7J
問2 ★やや難
解答：
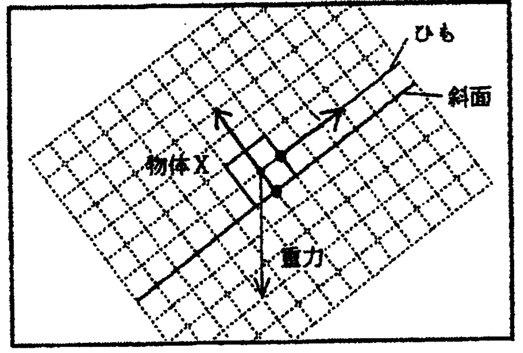
解説：
主語（力がはたらく相手）は「物体X」です。
力が働く方向に分解して、一つずつ考えていきます。
まず鉛直下向きには、重力（①）が働きます。
物体は斜面上にあるので、物体にはたらく重力の分力として、斜面方向の分力と斜面に垂直方向の分力に分解できます。
ただし、分力であるので物体に働く力として書きません。
物体は静止している、つまり力がつり合っているので、
物体にはたらく重力の斜面方向の分力＝糸が物体を引く力の大きさ（②）
物体にはたらく重力の斜面に垂直方向の分力＝物体にはたらく垂直抗力（③）
であるので、①〜③を書いて答えが得られます。
問3 ★やや難
解答：イ
解説：
三平方の定理の知識が必要な問題で、『塾技 理科80』に普通に載っています。
現段階では解答不能な問題です。11月段階では三平方の定理は習っていないでしょう。
しかし公立高校入試本番では、こういうレベルの問題も必ず解けるようになっておいてください。
問2の考察より、物体にはたらく重力の斜面に垂直方向の分力＝物体にはたらく垂直抗力の大きさは4マスに相当し、物体にはたらく重力の斜面方向の分力＝糸が物体を引く力の大きさの大きさは3マスに相当します。
これより、3：4：5の直角三角形となるので、
物体にはたらく垂直抗力の大きさ＝重力[N]×4/5＝7.5N×4/5＝1.5×4＝6.0N
物体にはたらく重力の斜面方向の分力＝糸が物体を引く力の大きさの大きさ＝重力[N]×3/5＝7.5N×3/5＝1.5×3＝4.5N
となります。
問4
解答：36cm
解説：
仕事の原理より、
物体Xを斜面にそって0.6m引き上げた仕事の大きさ＝物体Xを垂直方向にx(m)引き上げた仕事の大きさ
が成り立ちます。方程式を解くと、
2.7J＝7.5N×x
2.7N・m＝7.5N×x
x＝2.7/7.5ｍ＝2.7/7.5×100cm＝9/25×100＝9×4＝36cm
大問6 体循環と肺循環（やや難）
問1 ★難
解答：エ
解説：
血液循環を正しく理解できていないと解けない問題です。
血液は、全身→大静脈→右心房→右心室→肺動脈→肺→肺静脈→左心房→左心室→大動脈→全身、と流れていきます。
次に、与えられた数値を単位を付けてまとめます。
ヒトの体内の血液量＝4900cm3
心臓の拍動の回数＝70回/分
左心室から送り出される血液量＝70cm3/回
右心室から送り出される血液量＝70cm3/回
より、
左心室から1分当たりに送り出される血液量＝70cm3/回×70回/分＝4900cm3/分
右心室から1分当たりに送り出される血液量＝70cm3/回×70回/分＝4900cm3/分
より、
左心室から全身を巡って心臓（左心房）へ戻るのに要する時間＝4900cm3÷4900cm3/分＝1分＝60秒
右心室から全身を巡って心臓（右心房）へ戻るのに要する時間＝4900cm3÷4900cm3/分＝1分＝60秒
よって、選択肢エが正解です。
左心室から全身を巡って心臓（右心房）へ戻るのに要する時間に、右心室→肺→左心房と血液が巡るのに要する時間を加えて60秒になるので、左心室から全身を巡って心臓（右心房）へ戻るのに要する時間は、明らかに60秒より短いと言えます。
よって、選択肢イは誤りです。
問2
解答：A･･･肺胞、理由･･･空気に触れる表面積が大きくなるため。（例）
解説：
略。
問3
解答：①･･･エ、②･･･ア
解説：
ア：じん臓でこし出されて、血液中の尿素は減少します。ブドウ糖とタンパク質は減少しません。
イ：細胞呼吸によりアミノ酸が分解されるとアンモニアが発生し、肝臓で無毒の尿素に変えられます。
ウ：肺の肺胞でのガス交換により、酸素は増加します。
エ：肺の肺胞でのガス交換により、二酸化炭素は増加します。
オ：細胞呼吸により、養分（ブドウ糖、アミノ酸、脂肪酸＋モノグリセリド）は減少します。
大問7 体細胞分裂と減数分裂（標準レベル）
問1
解答：A･･･体細胞、B･･･減数
解説：
図1は無性生殖であるので、体細胞分裂が行われ、親と全く同じ遺伝子型になります。
図2は有性生殖であるので、減数分裂により染色体が半分に分かれ、それぞれ別々の生殖細胞に行きます。
問2
解答：P･･･生殖（細胞）、法則･･･分離（の法則）
解説：
略。
問3
解答：栄養（生殖）
解説：
略。
問4
解答：X･･･オ、Y･･･ウ、オ
解説：
・X
無性生殖であるので、親と同じ遺伝子型になります。
よって、選択肢オが正解です。
・Y
片親の遺伝子型をAa、もう片親の遺伝子型をaaとすると、子の遺伝子型の組み合わせは、Aaとaaとなります。
よって、選択肢ウまたはオが正解です。
大問8 地震（標準レベル）
問1
解答：
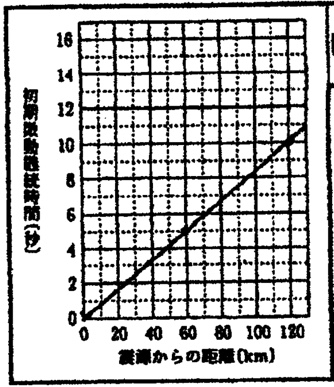
関係･･･比例
解説：
（震源距離、初期微動継続時間）＝A（36km、3秒）、B（60km、5秒）、C（120km、10秒）
初期微動継続時間は震源距離に比例するので、原点とこの3点を結んで直線を書きます。
問2
解答：6km/s
解説：
地震の問題は、表をタテに読むのが鉄則です。
A地点とB地点を見ると、P波は24km（60km – 36km）を4秒（16:10.22 – 16:10.18）で移動しているので、
P波の速度[km/s]＝24km/4s＝6km/s
問3
解答：16時10分12秒
解説：
地震が発生するとP波とS波が同時に発生します。
A地点の震源距離は36km、P波の速度は6km/sより、P波は震源からA地点までを6秒（36km÷6km/s）で移動します。
A地点のP波到達時刻は16時10分18秒より、地震発生時刻はその6秒前の16時10分12秒です。
問4
解答：ア、エ
解説：
震度は10段階（「震度０」「震度１」「震度２」「震度３」「震度４」「震度５弱」「震度５強」「震度６弱」「震度６強」「震度７」）で示されます。
大問9 火成岩（易）
問1
解答：火山（岩）
解説：
略。
問2
解答：等粒状（組織）
解説：
略。
問3
解答：大地が上昇（隆起）して削られ（浸食され）、火成岩Cが地表に現れたから。
解説：
略。
あまり問われることが無いタイプの問題ですが、本問を通じて覚えておきましょう。
問4
解答：①･･･ア、②･･･ア
解説：
・①
観察の結果より、火成岩Aの色は全体的に白っぽいことから、マグマに二酸化ケイ素が多く含まれ、粘り気が強いと考えられます。
・②
マグマの粘り気が強いと爆発的噴火となり、溶岩ドームが形成されます。
大問10 遺伝（標準レベル）
問1
解答：顕性（優性）形質
解説：
略。
問2 ★やや難
解答：約3倍
解説：
問われていることは定期テストレベルですが、問い方がややこしい問題です。
表より、
・丸×しわ
子に現れた形質がすべて丸より、純系の丸の遺伝子型をAA、純系のしわの遺伝子型をaaとおくと、
AA×aa→Aa、Aa、Aa、Aa
とすべて丸型になります。
子どうしを自家受粉させると、孫の遺伝子型の組み合わせは、
Aa×Aa→AA、Aa、Aa、aa
となり、丸（優性形質）：しわ＝3：1となります。
理論的にこの数値になることに留意すると、
丸(優性形質)：しわ＝5474：1850≒3：1
より、優性形質の個体数は、対立形質である劣性形質の約3倍となります。
黄色×緑色、高い×低いの場合も、同様に考えて、優性形質の個体数は、対立形質である劣性形質の約3倍となります。
問3
解答：AA
解説：
問2解説参照。
問4 ★やや難
解答：Bb
解説：
子に現れた形質がすべて黄色より、黄色の遺伝子Bは優性形質、緑色の遺伝子bは劣性形質です。
劣性形質どうしを組み合わせて、優性形質が現れているので、片親の遺伝子型は必ずBbです（『塾技 理科80』で強調されている、重要ポイントです。）。
この段階で、固体Xの遺伝子型はBb（黄色）だと分かります。
緑色の遺伝子型は必ずbbであるので、
Bb×bb→Bb、Bb、bb、bb
Bb：bb＝2：2＝1：1
となるので、答えが正しいと確信が持てます。
