
👉教師紹介・料金
※授業料1回1,500円+交通費(コミコミ最大3,000円)・入会金なし・お好きな日時に受講・3回のお試し期間あり(無料教材あり)
>>的中率60%以上!今年度の北海道公立高校入試「理科」はここが狙われる!家庭教師のそらの予想出題分野
■ボーダー(合格)ライン・最低点の推移
>>北海道公立高校入試の道コン最低点推移のランク別まとめ
■平均点推移と予想
>>北海道公立高校入試の平均点推移・各科目の正答率・人数分布・平均点予想まとめ
■一般入試の合否判定の手順
>>【最新版】北海道公立高校一般入試の合否判定の手順の詳細まとめ
■一般入試(全体・学区外受験)の最終倍率推移
>>北海道公立高校入試の一般入試(全体・学区外受験)の最終倍率推移
北海道公立高校入試過去問はこちら
★過去問
★模擬テストとリスニング対策
※模擬テストは1教科のみ表示。Amazonなどでは5教科すべて販売されています。
北海道教育委員会の講評(公式)
北海道教育委員会が公表した、令和二年度『入学者選抜状況報告書』の「学力検査問題等研究協議会における主な意見」よると、2020年の理科の講評は、以下の通りです。
<北海道教育委員会の講評>
理科では、観察・実験の結果を分析・解釈する問題が出題されており、難易度についてもバランスよく出題されていた。
今後も問題を正確に読み取るための時間の確保を考慮しながら科学的な見方や考え方を問う問題について、一層充実させるよう検討してほしい
令和二年度『入学者選抜状況報告書』 より
2020年の北海道公立高校入試「理科」の平均点
今年度の北海道公立高校入試の平均点と、人数分布は以下の通りです。
★学校裁量問題合格者の各科目の平均点(2020年)
| 国語 | 数学 | 英語 | 社会 | 理科 | 合計 | |
| 2020 | 39.0 | 30.9 | 38.1 | 31.5 | 25.7 | 186.5 |
※理科と社会は全合格者の平均点
★学校裁量問題受験者の各科目の正答率と人数分布(2020年)
| 受験者数 | 得点分布比率(%) | ||||||||
| 0〜25 | 26〜30 | 31〜35 | 36〜40 | 41〜45 | 46〜50 | 51〜55 | 56〜60 | ||
| 国語 | 11659 | 7.8 | 10.1 | 17.0 | 21.8 | 22.1 | 14.5 | 5.9 | 0.9 |
| 数学 | 11659 | 34.4 | 17.5 | 16.6 | 13.5 | 8.8 | 5.4 | 2.6 | 1.2 |
| 英語 | 11659 | 15.0 | 11.5 | 15.6 | 16.7 | 15.5 | 13.1 | 10.1 | 2.8 |
| 社会 | 26611 | 33.5 | 11.1 | 12.3 | 12.5 | 12.6 | 10.5 | 6.0 | 1.6 |
| 理科 | 26611 | 48.5 | 12.7 | 13.1 | 12.4 | 8.1 | 4.0 | 1.1 | 0.1 |
※理科と社会は全合格者の受験者数と得点分布比率
>>北海道公立高校入試の平均点推移・各科目の正答率・人数分布まとめ
大問1 小問集合
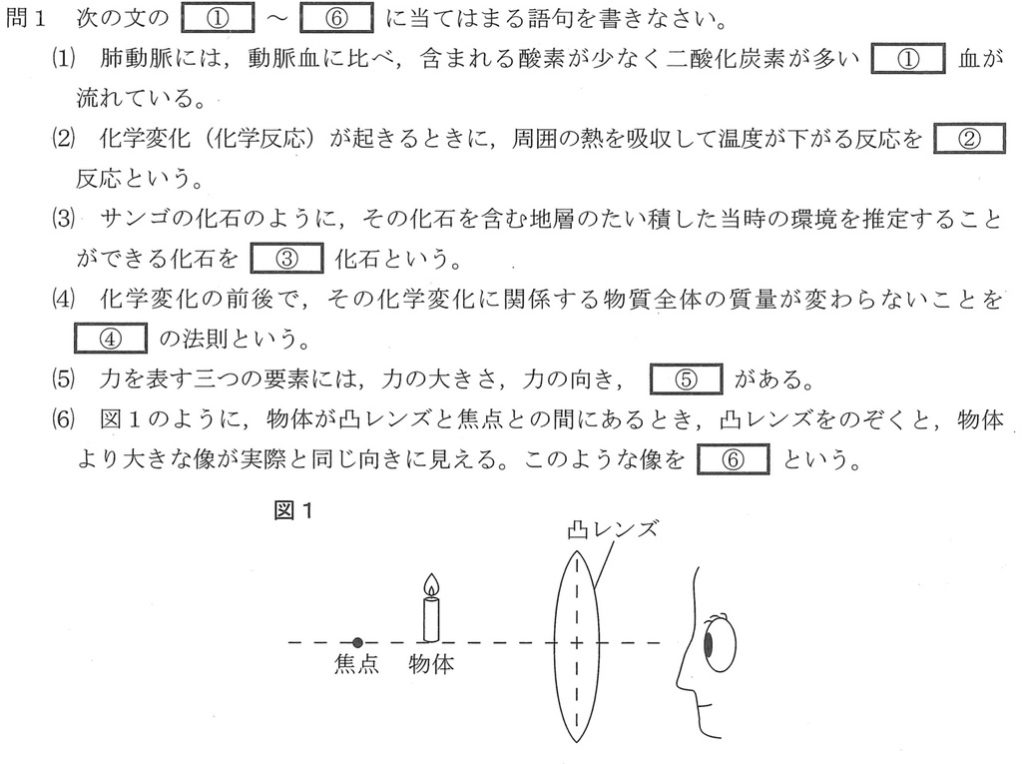

問1(1)①<正答率 84.6%>
(答)静脈
(解説)
血液循環には、肺循環と体循環の2つがあります。
肺循環では、全身を巡ってきた酸素の少ない血液である静脈血が、心臓から肺に肺動脈を通じて送られ、肺胞の毛細血管でガス交換が行われ、酸素の多い動脈血となったあと、肺から心臓に肺静脈を通じて送られ、心臓の左心室から大動脈を通じて全身に送られます。
問1(2)②<正答率 81.5%>
(答)吸熱
(解説)
熱分解など、周囲の熱を吸収して化学反応を起こす反応を吸熱反応といいます。
理科での暗記のコツは、少ない方を覚えることです。
吸熱反応は多数ありますが、発熱反応は
・塩化アンモニウムと水酸化ナトリウムの反応(アンモニアが発生)
・鉄と硫黄の化合
の2つを覚えればOKです。
問1(3)③<正答率 68.4%>
(答)示相
(解説)
「サンゴの化石」「環境」ときたら、示相化石です。
サンゴの化石があると、この地域はかつて暖かくて浅い海があったことが分かります。
問1(4)④<正答率 86.0%>
(答)質量保存
(解説)
質量保存則を活用するのが、石灰石と塩酸を加えて発生する二酸化炭素の定量です。
『塾技 理科80』レベルの問題が解けるようになれるよう、これから頑張りましょう。
問1(5)⑤<正答率 30.3%>
(答)力のはたらく点(作用点でも可)
(解説)
解答例のとおりです。
問1(6)⑥<正答率 68.2%>
(答)虚像
(解説)
物体が凸レンズの焦点の内側にあるとき、スクリーンに倒立実像は映らず、凸レンズを通して物体を見ると、物体より大きな像である正立虚像が見えます。
凸レンズの問題は、過去10年間ずっと出ていないので、注意が必要です。
問2 ①<正答率 60.6%>
(答)肝臓
問2 ②
(答)じん臓
(解説)
血しょうを通じて送られたアミノ酸は窒素を含むため、細胞呼吸で燃焼するとアンモニアを生じます。
アンモニアはそのままでは大変有毒なので、いちど肝臓に送られて尿素に変えられたあと、じん臓でこしだされ尿として排出されます。
問3 ①<正答率 41.4%>
(答)斑晶
問3 ②
(答)石基
(解説)
マグマ(地中にある)が冷え固まってできた岩石を火成岩といい、その冷え方により火山岩と深成岩に大別されます。
火山岩は、マグマが地表や地表付近で急冷されてできた岩石で、非常に細かい結晶やガラスからなる石基と、石基に散らばって見える大きな結晶である斑晶からなります。これを斑状組織といいます。
深成岩は、マグマが地下深くでゆっくり冷え固まってできた岩石で、ゆっくり冷えるために大きな結晶ができます。これを等粒上組織といいます。
マグマの冷え方により結晶のサイズが異なるのは、ミョウバンの水溶液実験で分かります。
問4<正答率 44.4%>
(答)エ、カ
(解説)
胞子で増えるのは、シダ植物とコケ植物です。
シダ植物として、イヌワラビ、スギナ、ゼンマイなどがあります。
コケ植物として、ゼニゴケ、スギゴケなどがあります。
シダ植物は、イヌワラビの場合、葉の裏側にある胞子のうが乾いて裂けて胞子が飛びだし、前葉体ができます。雨の日に前葉体の雄器から精子が泳ぎ出て、前葉体の雌器にある卵に受精して幼いシダができて、個体を増やします(無性生殖→有性生殖)。
コケ植物は、雄株と雌株に分かれ、雨の日に雄株から精子が泳ぎ出て雌器にいって受精し、雌器から胞子が作られ、胞子のうが乾いて裂けて胞子が飛びだし、雄株。雌株となります。
問5<正答率 57.3%>
(答)C
(解説)
酸化銅の炭素による還元の化学反応式です。
実験方法と、炭素を増やすと折れ線曲がったグラフになる理由を押さえておきましょう。
このほか、酸化銅の水素による還元も重要です。
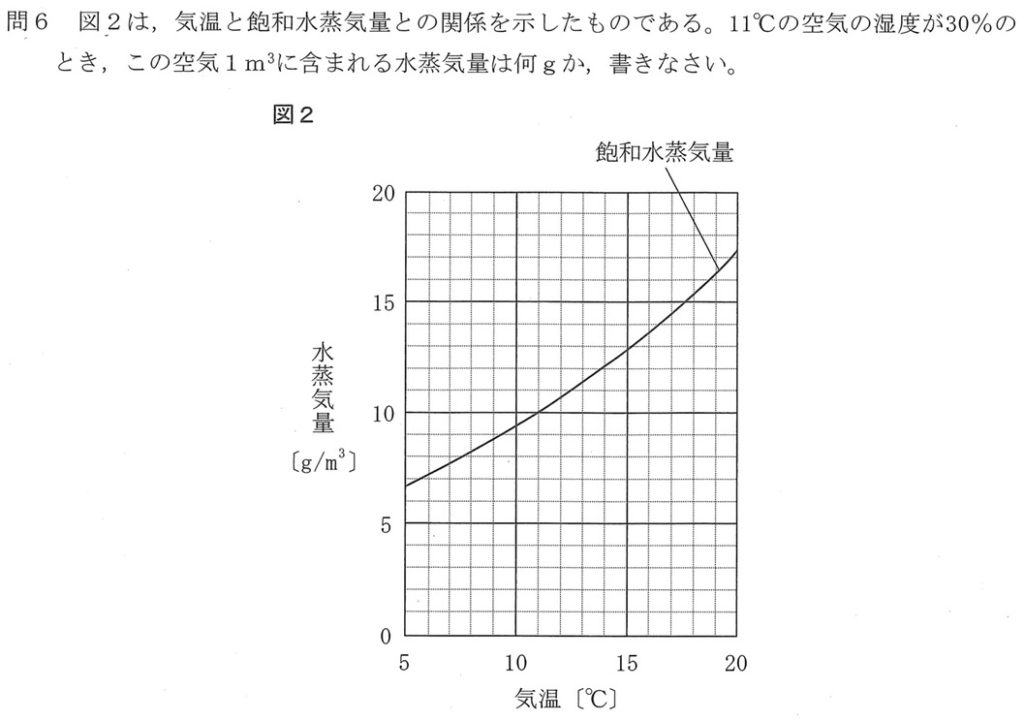
問6<正答率 52.1%>
(答)3(g)
(解説)
水蒸気とは、気体の状態の水で目に見えません。
湯気は、水蒸気が冷えてできた水の粒です。混同しないように。
空気とは、水蒸気を含むことができる入れ物で、水蒸気を何g含むことができるのかを表す単位として、g/m3を用います。
g/m3は、1m四方の立方体(体積1m3)に含むことができる水蒸気量(g)というイメージです。
体積1m3の立方体の空気が限界まで含むことができる水蒸気量(g)を飽和水蒸気量(g/m3)といい、
温度が上がると飽和水蒸気量(g/m3)も上がります。
空気は温度が上がると、水蒸気をより多く含むことができるからです。
飽和水蒸気量(g/m3)に対してどのくらい水蒸気(g)が含まれているのかを示す指標が湿度です。
以上の知識を元に問題を解きます。
飽和水蒸気量のグラフより、11℃の空気では、10g/m3まで水蒸気を含むことができます。
これを高さ10の入れ物と見立てると、この入れ物に30%の水蒸気が入っているので、
10g/m3×30%=10g/m3×0.3=3g/m3
の水蒸気が11℃の空気に含まれています。
1m3あたりですと、
3g/m3×1m3=3g
の水蒸気が含まれています。
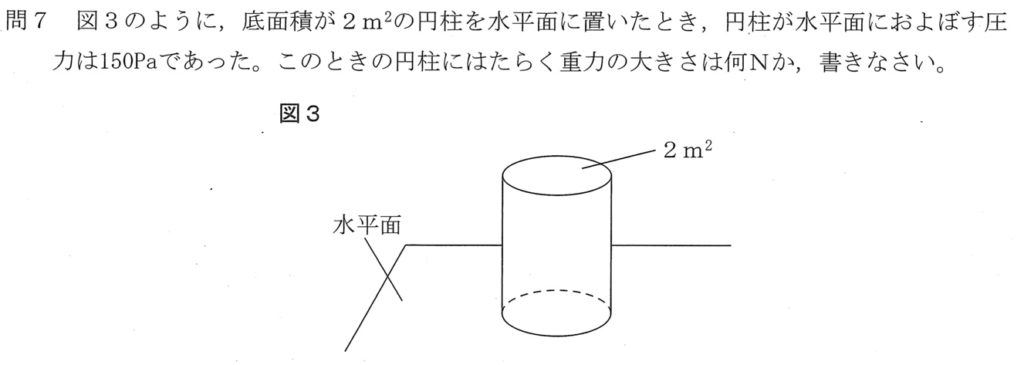
問7<正答率 44.2%>
(答)300(N)
(解説)
単なる単位計算の問題です。
圧力が150Pa=150N/m2、面積が2m2より、重力(N)は、
150N/m2×2m2=300N
大問2 身のまわりの物質(中1・化学分野)


★家庭教師のそらの生徒の授業にて、プラスチックの部分が的中しました!!
問1(1) ①<正答率 49.7%>
(答)最も低いところ(「平らなところ」でも可)
問1(1) ②
(答)イ
(解説)
★レベル:レベル1(超基本問題 絶対に落とせない問題)
メスシリンダーは、以下のようにして測定します。
① 目は液面の水平部分に
② 最小メモリの1/10まで目分量で読みとる
問1(2) 密度<正答率 47.7%>
(答)2.7(g/cm3)
(解説)
★レベル:レベル2(基本問題 落とせない問題)
単なる単位計算の問題です。
求めるのは、g/cm3です。
問題文に「質量がいずれも13.5gの3種類の金属A〜Cを用意した。」とあるので、金属Aの質量は13.5gです。
金属Aの体積(cm3)ですが、
問題文に「あらかじめ50.0cm3の水を入れておいたメスシリンダーAを入れ」とあり、「表」より金属Aをメスシリンダーに沈めたときの読み取った体積が55.0cm3とあるので、差をとって、金属Aの体積は 55.0cm3 – 50.0cm3 = 5.0cm3です。
質量(g)と体積(cm3)が分かったので、あとは密度(g/cm3)の単位に代入して終わりです。
金属Aの密度(g/cm3)=13.5g/5.0cm3=2.7g/cm3
問1(2) 記号<正答率 48.7%>
(答)カ
(解説)
★レベル:レベル3(標準問題 差が付く問題)
金属Aの密度を求めた方法に習い、金属Bと金属Cの密度を求めて比較することで、金属A,B,Cの密度の大小関係を求めることができます。
しかし、この方法では時間がかかり過ぎるのでやめましょう。
密度の単位はg/cm3で、密度は質量(g)に比例し、体積(cm3)に反比例すると読むことができます。
質量(g)が分子にあるので、質量(g)が増加すると密度(g/cm3)も増加し、
体積(cm3)が分母にあるので、体積(cm3)が増すと密度(g/cm3)が減少するからです。
この考え方を用いて、本問を解いてみましょう。
問題文に「質量がいずれも13.5gの3種類の金属A〜Cを用意した。」とあるので、質量(g)が金属A,B,Cで同じで異なるのは体積(cm3)のみです。
ゆえに、体積(cm3)が大きいほど密度(g/cm3)が小さくなります。
「表」より、体積(cm3)の大小関係はA>B>Cと読み取れるので、密度(g/cm3)の大小関係はc>b>aとなります。
さらに進んで、異なる2つの物質において、
体積(cm3)が同じとき、密度の比=質量比となり、
質量(g)が同じとき、密度の比=体積比の逆比となることも押さえておきましょう。
圧力(N/m2)の応用問題で活用できます。
問2(1) ①<正答率 18.7%>
(答)樹脂
問2(1) ②<正答率 17.6%>
(答)イ
問2(1) ③
(答)ア
(解説)
★レベル:レベル2(基本問題 落とせない問題)
②
問題文の「実験2」の「図2」にボトルの表記にPETとあるので、ペットボトルのボトルはポリエチレンテレフタレートからできていると言えます。
プラスチックの種類として、5つ覚えましょう。
PET:頭文字から「ポリ(P)エチレン(E)テレフタレート(T)」と読み、燃やすと多少のススが出ます
PS:頭文字から「ポリ(P)スチレン(S)」と読み、燃やすとススがたくさん出ます
PVC:頭文字から「ポリ(P)塩化(C)ビニル(V)」と読みます
PE:頭文字から「ポリ(P)エチレン(E)」と読み、密度が1.0g/cm3(4℃の水)より小さいので、水に浮きます
PP:頭文字から「ポリ(P)プロピレン(P)」、密度が1.0g/cm3(4℃の水)より小さいので、水に浮きます
PETとPSは燃やすとススが出る、PEとPPは水に浮く、と覚えるとよいでしょう。
③
先ほど紹介した5つのプラスチックの知識を用いると、容易に答えが出せます。
問題文の「実験2」の「図2」から、本問で登場するプラスチックは、PETとPPとPEの3つです。
PPとPEは水に浮き、PETは水に沈みます。
問題文の「実験2[3]」に「水が入ったビーカーに、S〜Uを入れたところ、TとUは浮き、Sは沈んだ。」とあるので、
PETはプラスチックの小片Sと断定できます。
プラスチックの小片TとUは、「実験2[3]」を読んだ段階では、PPかPEか区別できません。
問2(2)<正答率 9.5%>
(答)100/3e(cm3)
(解説)
★レベル:レベル3(標準問題 差が付く問題)
多くの子が出来ないと思われるのでレベル3としましたが、『塾技 理科80』まで終わらせた子なら、超簡単な問題だと思います。
本問は、単なる単位計算の問題です。
与えられた情報は、水50.0cm3、水の密度1.0g/cm3、エタノールの密度e(g/cm3)で、
問われているのは、エタノールの体積(cm3)です。
問題文の「実験2[2]」に「水とエタノールの質量の比が3:2となるように混合した液体」とあるので、
水とエタノールの密度(g/cm3)から質量(g)を算出し、質量比の比例式を立式します。
エタノールの体積(cm3)をxとおくと
1.0g/cm3×50.0cm3:e × x=3:2
⇔ 3ex=100
⇔ x=100/3e(cm3)
『塾技 理科80』を終わらせた子なら、この問題は10秒で解けたはずです。
問2(3)<正答率 15.1%>
(答)T>Z>U>E
(解説)
★レベル:レベル3(標準問題 差が付く問題)
国語の問題です。
問題文の「実験2[3]」に「水が入ったビーカーに、S〜Uを入れたところ、TとUは浮き、Sは沈んだ。」とあるので、プラスチックの小片Sは除外されます。
問題文の「実験2[4]」に「エタノール(E)が入ったビーカーに、S〜Uを入れたところ、すべて沈んだ」とあるので、
密度の大小関係は、T,U>E、となることが分かります。
問題文の「実験2[5]」に「液体(Z)が入ったビーカーに、S〜Uを入れたところ、Uは浮き、SとTは沈んだ」とあるので、
先ほど出した密度の大小関係は、T>U>Eと書け、
さらに液体(Z)にプラスチックの小片Uが浮き、プラスチックの小片Sが沈んだことから、密度の大小関係は、T>Z>U>Eと書けます。
本問は、ある固体が、それより密度の大きい液体に浮き、密度の小さい液体に沈む、という前提知識が必要ですが、
それに加えて、問題文を素直に読んで機械的に答えを導く国語力が要求されています。
大問3 地球と宇宙(中3・地学分野)


★ブログと家庭教師のそらの生徒の授業にて、全て的中しました!!
問1(1)<正答率 49.2%>
(答)エ
(解説)
★レベル:レベル1(超基本問題 絶対に落とせない問題)
天体望遠鏡を用いた太陽の観察では、以下の3つを押さえておきましょう。
・太陽投影板上の黒点が東から西(正面から見て右から左)に移動→太陽が自転をしていることが分かる
・太陽投影板上の黒点が周辺部ではだ円形になった→太陽が球形をしていることが分かる
・太陽投影板の像が数分で東から西(正面から見て右から左)に移動していった→地球が自転しているため(1時間に15°)
ここまでは知っていて当たり前の基礎知識です。
これに加えて、黒点の直径が地球の何倍になるかを示した式も、理解した上で押さえるべきです。
以上の知識を踏まえて、選択肢を見ていきましょう。
・ア
季節によって昼の長さが異なるのは、地球が地軸の北極側を公転面に垂直な線に対して地軸を23.4°傾けて、太陽の周りを反時計回りに公転しているからです。
天球上において、夏至は南中高度が高くなるため、昼が長く夜が短くなります。冬至は南中高度が低くなるため、昼が短く夜が長くなります。
同一地点においては、南中高度が高くなると昼が長くなり、南中高度が低くなると昼が短くなります。
透明半球を用いた観察実験から、このような結論が得られます。
天体上においても、北半球の同一地点において、夏至は地軸の北極側を太陽に傾けているため、南中高度が高くなり、昼の線が夜の線よりも長くなり、昼が夜より長くなります。
逆に冬至は地軸の北極側を太陽と反対方向に傾けているため、南中高度が低くなり、昼の線が夜の線よりも短くなり、昼が夜より短くなります。
しかし、たとえば夏至において、同一経度で緯度が高くなると、南中高度が低くなるが昼の長さが長くなり、日の出が早くなります。
これは、天体上で図示することで分かります。
・イ
さそり座は季節の星座の一つで、夏至の日に真夜中に南中します(天体上で考えてください)。
季節の星座は、太陽と反対方向にあるとも言えます。
星座は恒星の集まりなので、動きません。
しかし地球が太陽を中心に反時計回りに公転して冬至になると、さそり座が太陽と同じ方向に位置してしまうため、太陽に遮られて観測できなくなります。
なお、冬至の日に真夜中に南中する星座は、オリオン座です。
・ウ
透明半球を用いて太陽が動いて見える道筋を観測すると、
夏至では太陽は真東より北寄りから昇り、真西より北寄りに沈みます。このため昼が長く夜が短くなります。
春分・秋分では、太陽は真東から昇り、真西に沈みます。このため昼と夜の長さが同じくなります。
この事実は、天体上において、地球が地軸の北極側を公転面に垂直な線に対して地軸を23.4°傾けて、太陽の周りを反時計回りに公転しているからです。
・エ
星の日周運動のはなしをしています。
地球は地軸の北極側から見て、反時計回り(西から東)に自転しています。
地球の自転周期は、1日・24時間で360°です(平均太陽日の考え方では、地球の自転周期は約23時間56分になります)。
つまり、1時間に15°西から東に自転しています。
そのため、公転しない星と太陽は、1時間に15°東から西に一定の速度で動いて見えます。
これを見かけの動きといいます。
なお、選択肢に「オリオン座が、その日の真夜中に南中した。」とあるので、冬至の日に観測したと考えられます。
問1(2)<正答率 17.6%>
(答)
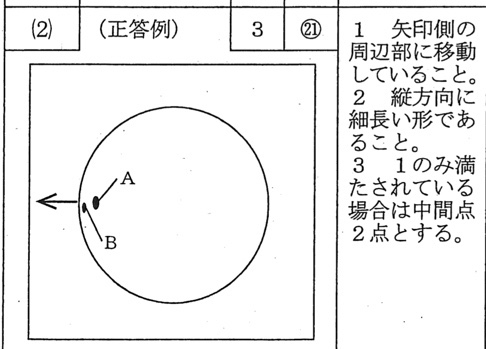
(解説)
★レベル:レベル2(基本問題 落とせない問題)
多くの塾で難しいと言われた問題ですが、天体の方角を根拠を踏まえて捉えるよう務めてきた子なら、この問題は非常に易しい問題だと感じたはずです。
天体上において、太陽は反時計回りに自転します。
太陽の自転方向は東から西で、太陽投影板に写すと、ちょうど鏡に写したときと同じく、左右逆になります。
家庭教師のそらの生徒限定の理科の教材にある以下の図を見ると、分かるはずです。
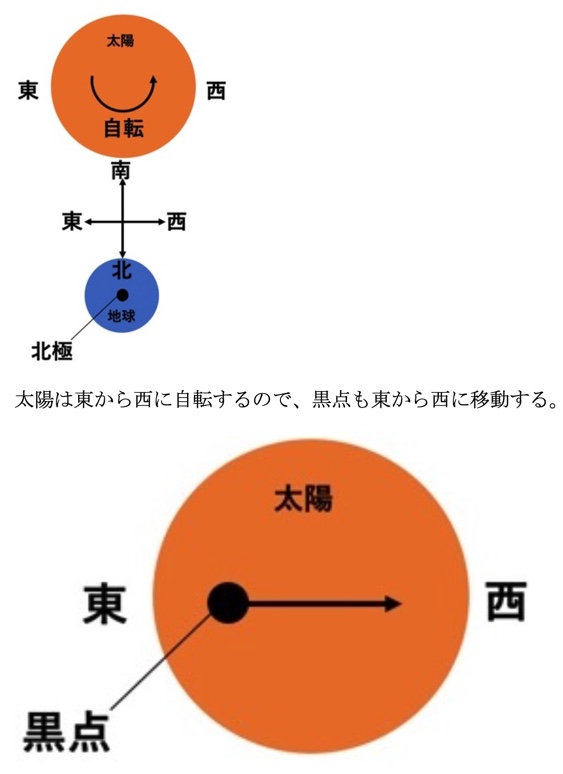

これから、問題文の「図1」の記録用紙の左側が西、右側が東で、
毎日同一時刻に観測すると、黒点AとBは右から左(東から西)に移動します。
また、太陽は球形をしているため、太陽投影板上の黒点が周辺部ではだ円形になります。
問題文の「観察1[2]」に「周辺部に移動した黒点A,Bを観察し」とあるので、5日後に黒点AとBは左端にだ円形になって存在しています。
黒点は太陽の同一地点にあるので、黒点Bが黒点Aより左側にあります。
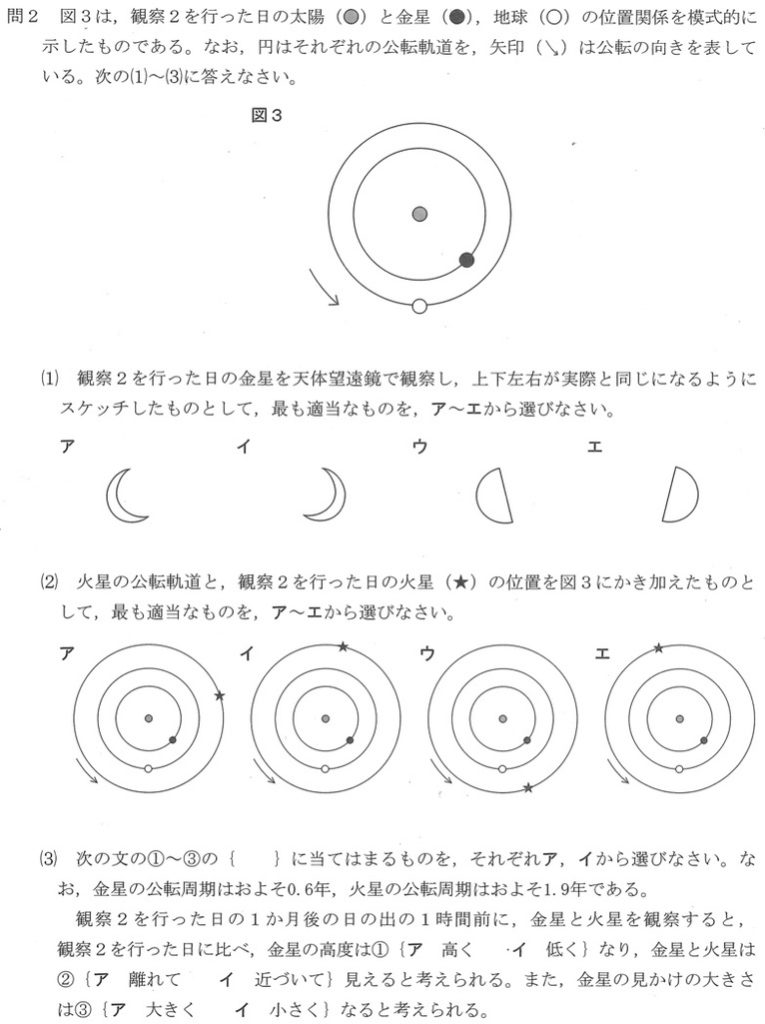
問2(1)<正答率 37.0%>
(答)ウ
(解説)
★レベル:レベル2(基本問題 落とせない問題)
問題文「図3」より、金星は明けの明星(明け方東の空に見える)に位置しており、問題文「図2」と整合性が取れています。
問題文に「金星を天体望遠鏡で観察し、上下左右が実際と同じになるようにスケッチした」とあるので、金星を肉眼で見たものを選択肢から選びます。
図3より、地球から金星の公転軌道に対する接線上に金星が位置していることが分かるので、金星は左半分が光って見えます。
なおこのとき、太陽-地球-金星のなす角である離角が最大となり、金星を最も長い時間見ることができます。
金星の満ち欠けの仕方ですが、「外合から、左から欠けて大きくなり、内合後、左から満ちて小さくなる」と覚えるとよいでしょう。
問2(2)<正答率 50.8%>
(答)ア
(解説)
★レベル:レベル2(基本問題 落とせない問題)
問題文の「観察2」に「日の出の1時間前に、金星と火星を観察し」とあり、「図2」の空にて火星がほぼ南東に見えていることを抑えましょう。
次に、「図2」の空を天体上で表したものを選択肢ア〜エから見ると、選択肢アが正しいことが分かります。
選択肢イだと火星は北東の空に、選択肢ウだと火星は南西の空に、選択肢エだと火星は北東の空に見えるので、不適です。
問2(3) ①<正答率 20.1%>
(答)イ
問2(3) ②
(答)ア
問2(3) ③
(答)イ
(解説)
★レベル:レベル5(難問 捨ててOK)
本セットの中で、最高難度の問題です。
本問は、惑星の会合周期の考え方を知らないと、解けません。
太陽系の8つの惑星は全て、太陽を中心として反時計回りに公転しており、太陽からの距離が長いほど公転周期(太陽の周りを1周360°公転するのにかかる時間)も長くなります。
星と太陽は公転しないため、地球から見て規則的に動いて見えますが、惑星は相互に動くため、地球から見て不規則な動きをして見えます。
このため、惑星は「惑う星」という意味で名付けされています。
①
まず、「観察2を行った日の1か月後」の金星と火星の回転角を求めます。
問題文に「金星の公転周期はおよそ0.6年、火星の公転周期はおよそ1.9年である」の条件を用いて、
・金星の回転角
0.6年×12か月/年:360°=1か月:x
⇔0.6:30=1か月:x ⇔ 0.6x=30 ⇔ x=300/6=50°
しかし、1か月間で地球も30°(360°/12か月×1か月=30°)回転しているので、
地球を固定すると、金星は20°(50° – 30°=20°)相対的に反時計回りに回転していることになります。
・火星の回転角
1.9年×12か月/年:360°=1か月:x
⇔1.9:30=1か月:x ⇔ 1.9x=30 ⇔ x=300/19°<30°
しかし、1か月間で地球も30°(360°/12か月×1か月=30°)回転しているので、
地球を固定すると、火星は約14°(300/19° – 30°=270/19° ≒ 14°)相対的に時計回りに回転していることになります。
(地球の方が回転速度が速いため、火星が近づいて見える)
これを、問2(2)の選択肢アを用いて図示すると、以下のようになります。
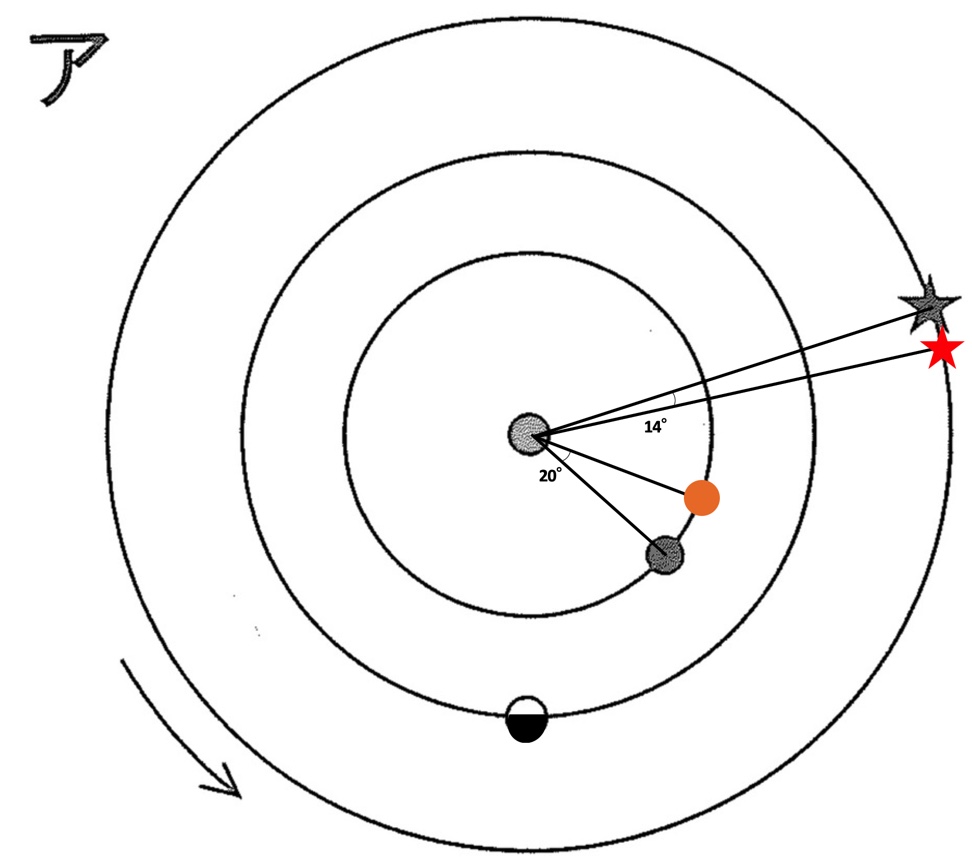
この図を踏まえて、1ヶ月前と1ヶ月後の金星の方位の変化を調べます。
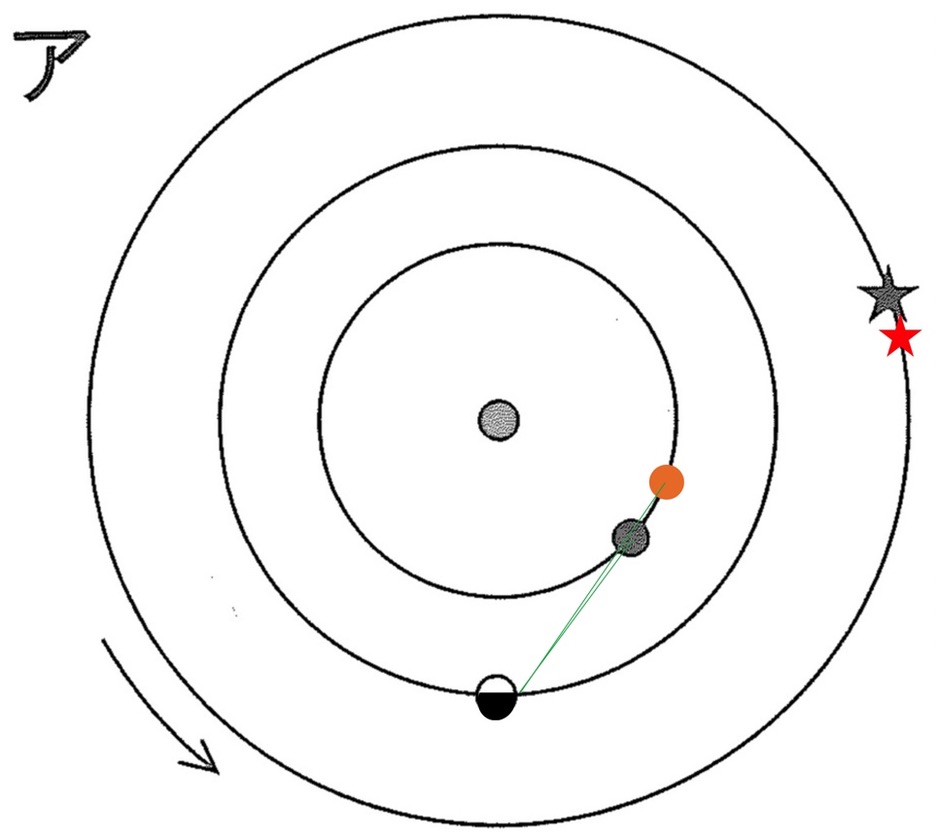
やや分かりづらいですが、同一時刻(日の出の1時間前)で、金星が1ヶ月前より東寄りに見えていることが分かります。
1日単位で考えると、金星は太陽や星と同じく、東から昇り、南の空に位置したとき高度が最大となり(南中高度)、西に沈みます。
これと「図2」より、金星の高度が低くなったと考えられます。
②
離角の考え方に基づき、1ヶ月前と1ヶ月後の金星と火星の位置関係を調べていきます。
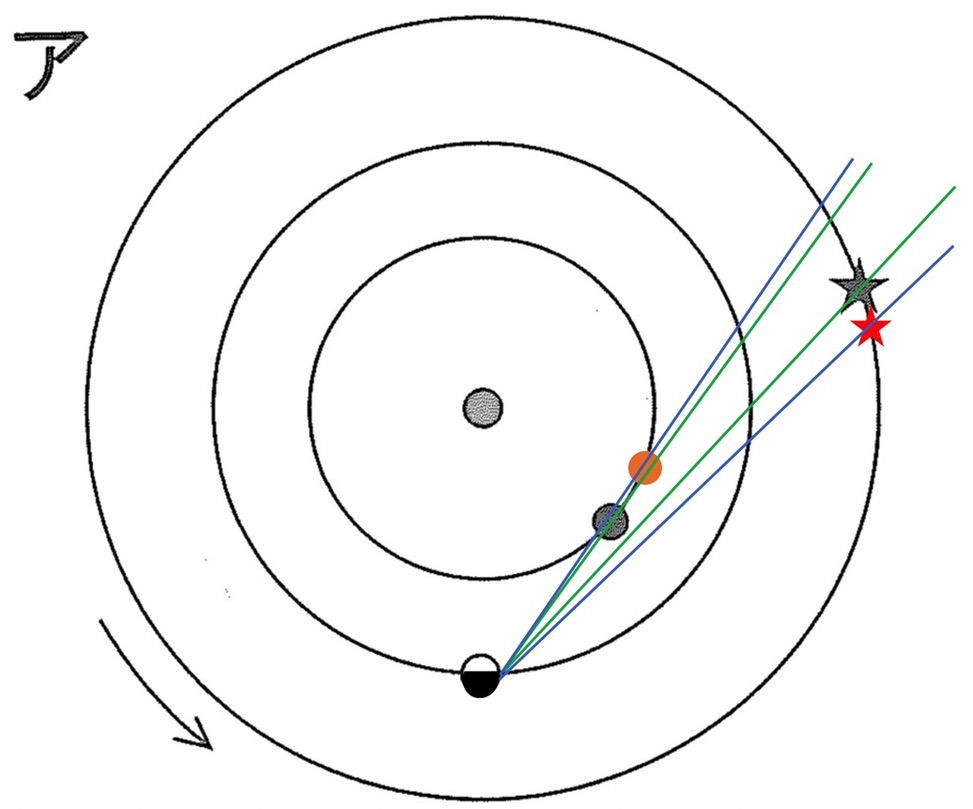
2本の緑色の線のなす角度が1ヶ月前の金星と火星の離れて見える距離、2本の青色の線のなす角度が1か月後の火星の離れて見える距離です。
明らかに2本の青色の線のなす角度の方が、2本の緑色の線のなす角度より大きいので、1か月後に金星と火星は離れて見えると考えられます。
③
解説①の図より、金星が地球から離れているため、金星の見かけの大きさは小さくなると考えられます。
これは簡単ですね。
大問4 電流とその利用(中2・物理分野)
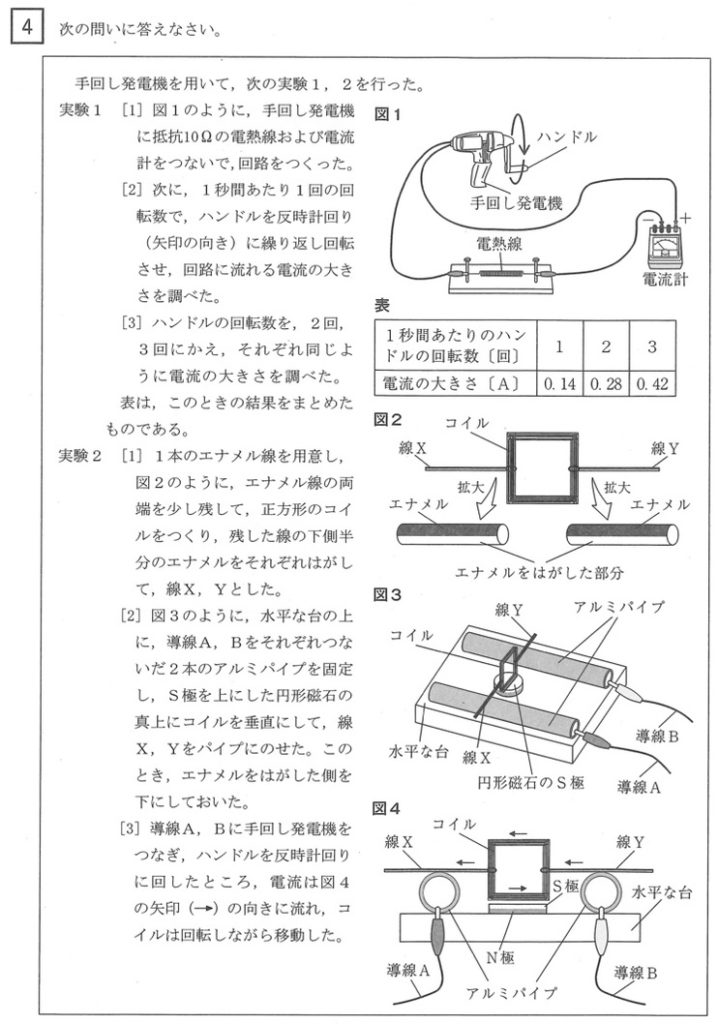

★家庭教師のそらの生徒の授業にて、全て的中しました!!
問1(1)<正答率 70.9%>
(答)1.4(V)
(解説)
★レベル:レベル2(基本問題 落とせない問題)
問題文で与えられている「表」を見ると、1秒間あたりのハンドルの回転数に比例して電流の大きさが増加していることから、オームの法則より、1秒間あたりのハンドルの回転数を電圧と見立てることができます。
「[2]のとき」、「表」から電流の大きさは0.14A、抵抗値が10Ωから、オームの法則を用いて電熱線に加わる電圧を算出できます。
オームの法則より、
V=I × R=0.14A×10Ω=1.4V
問1(2)<正答率 56.0%>
(答)ウ
(解説)
★レベル:レベル2(基本問題 落とせない問題)
問題文の「回路に流れる電流の大きさ」とは、回路全体を流れる電流の大きさより、合成抵抗を用いて解くパターンだと推測できます。
「図5」は直列回路より、回路全体の抵抗(合成抵抗)は、10Ω+10Ω=20Ωです。
問1(1)より、1秒間あたりのハンドルの回転数が1回のときが1.4Vに相当するので、1秒間あたりのハンドルの回転数が3回のときは3×1.4V=4.2Vに相当します。
オームの法則より、回路全体を流れる電流の大きさは、
V=I × R ⇔ I=V/R=4.2V/20Ω=2.1/10A=0.21A
問2(1) ①<正答率 30.5%>
(答)ア
(解説)
★レベル:レベル2(基本問題 落とせない問題)
『塾技 理科80』に載っている、右手のパーを使えば楽勝で解ける問題です。
「図4」より、磁界の向きは下向きです(磁界はN極から出てS極に戻る、と覚える)。
コイル上部に流れる電流の向きは左なので、右手のパーより、コイル上部にかかる力は、図3の線Xから線Yの方向に見て時計回りです。
コイル下部に流れる電流の向きは右なので、右手のパーより、コイル下部にかかる力は、図3の線Xから線Yの方向に見て時計回りです。
コイル上部と下部で、かかる力の向きが時計回りより、コイルは時計回りに回り始めます。
問2(1) ②
(答)ア
(解説)
★レベル:レベル1(超基本問題 絶対に落とせない問題)
物体に力が働かないと、物体は静止または等速直線運動を続けます。
これを慣性の法則といいます。
コイルに電流が流れてコイルに時計回りの力が働き、コイルは時計回りに回りはじめます。
しかしコイルに電流が流れなくなって力が働かなくなると、摩擦などの外的影響がなければ、コイルは動いていた時の速度を維持したまま、一定の速度で回転し続けます。
問2(2)<正答率 54.7%>
(答)磁石のN極を上にしておく(「磁石のS極を上にしたままコイルの上に持っていく」でも可)
(解説)
★レベル:レベル2(基本問題 落とせない問題)
コイルにかかる力の向きは、電流と磁界の向きの2つによって決まります。
本問では電流の向きが逆向きになり、磁界の向きが同じなため、力の向きが逆向きとなり、コイルは反時計回りに回転し始めます。
この条件下で実験結果と同じ向き、つまりコイルを時計回りに回転させるには、磁界の向きを逆向きにすればよいと推測できます。
ですが、入試は問題文が全てなので、問題文をきちんと最後まで読んでから判断を下しましょう。
問題文に「ただし、導線A、Bとアルミパイプのつなぎ方、および導線A、Bと手回し発電機のつなぎ方は、いずれも変えないものとする。」とあるので、
変えられるのは磁石の向きだけです。
これから、磁界の向きを逆向きにするために、磁石のN極を上にしておくとよいことが分かります。
問題文に素直に従えば、電磁力の知識がなくても答えが出せる問題ですね。
問2(3)<正答率 14.5%>
(答)イ
(解説)
★レベル:レベル4(やや難 出来たら大きく差が付く)
『塾技 理科80』に載っている、右手のパーをちゃんと使いこなせているかが試される問題です。
問2(1) ①の復習をします。
「図4」より、磁界の向きは下向きです。
コイル上部に流れる電流の向きは左なので、右手のパーより、コイル上部にかかる力は、図3の線Xから線Yの方向に見て時計回りです。
コイル下部に流れる電流の向きは右なので、右手のパーより、コイル下部にかかる力は、図3の線Xから線Yの方向に見て時計回りです。
コイル上部と下部で、かかる力の向きが時計回りより、コイルは時計回りに回り始めます。
しかし、コイルが4分の1回転すると、エナメル線のせいでコイルに電流が流れなくなります(ビニールは不導体)。
そのため、コイルに力が働くなりますが、慣性の法則より、コイルは等速直線運動を続けます。
ここでエナメル線をはがして同じ実験をすると、まずコイルは時計回りに回り始めます。
しかし、コイルが4分の1回転した後、図3の線Xから線Yの方向に見て、コイル左側の部分には左向きの力が、コイル右側の部分には右向きの力が働き、互いに引き合うため、力が釣り合い静止します。
よって、コイルが4分の1回転した後、回転が止まります。
大問5 生命の連続性(中3・生物分野)


問1(1)<正答率 73.6%>
(答)視野が広く(「見える範囲が広く」でも可)
(解説)
★レベル:レベル1(超基本問題 絶対に落とせない問題)
問題文に「プレパラートを顕微鏡のステージにのせ」とあるので、この観察で使用している顕微鏡は、ステージ上下式・鏡筒上下式顕微鏡です。
ステージ上下式・鏡筒上下式顕微鏡では、倍率(接眼レンズの倍率×対物レンズの倍率)が2倍、3倍、・・・となると、視野と明るさは1/4倍、1/9倍、・・・となります。
高倍率になるほど、視野が狭く暗くなるということです。
ゆえに、最初に低倍率で観察したほうが、視野が広く明るく見えるので、観察したいものが探しやすいです。
問1(2)<正答率 62.4%>
(答)イ
(解説)
★レベル:レベル1(超基本問題 絶対に落とせない問題)
体細胞分裂では、間期で染色体が2倍に複製され、その後細胞質分裂(前期・中期・後期・終期4つの分裂期)を経て細胞が分裂します。
「図1」の細胞Xは、核膜がとけて染色体が露出し、染色体が赤道面に並んでいるので、細胞質分裂の中期の状態です。
「図2」の細胞Yについて、問題文に「細胞Yは、細胞分裂直後の、2つの細胞のうちの1つである」とあるので、細胞Yは、図6の4種類の染色体を1本ずつ持ちます。
少し進んだ話として、細胞Yは4種類の染色体を1本ずつ持つので、核相n=4と表すことができます。
問2(1) 縦方向の長さ<正答率 12.8%>
(答)0.15(mm)
問2(2) のびた長さ
(答)0.1(mm)
(解説)
★レベル:レベル3(標準問題 差が付く問題)
国語の問題です。
(1)
実験1の「図2」より、4つ目の印は、根の先端から4mmのところにあります。
実験1の「図3」の根Bは、根の細胞の縦方向の長さ調べるためにあり、根の先端からの距離(mm)と、細胞の縦方向の長さ(mm)との関係を表したグラフが「図5」です。
図5の根Bのデータより、根の先端から4mmのところにある細胞の縦方向の長さは0.15mmだと分かります。
(2)
問題文に「[2]印を付けてから24時間後、図4のようにAの長さは〜」とあるので「図4」を見ると、「その細胞」すなわち印をつけた直後の根の先端から4つ目の印は、根の先端から10mmの位置にあることが分かります。
図5の根Bのデータより、根の先端から10mmのところにある細胞の縦方向の長さは0.25mだと分かります。
24時間の間に、印をつけた直後の根の先端から4つ目の印にある細胞は、0.15mmから0.25mmになっているので、0.10mm(0.25mm – 0.15mm=0.10mm 有効数字3桁であることに注意)伸びたことが分かります。
問2(2) ①<正答率 1.6%>
(答)オ
問2(2) ②
(答)カ
問2(2) ③
(答)ケ
(解説)
★レベル:レベル4(やや難 出来たら大きく差が付く)
国語の問題です。
①
「図4」より、1つ目の印をつけた部分から4つ目の印をつけた部分がよく伸びたことが分かります。
また実験[2]の問題文に「4つ目から10個目の印までの間は、印と印の間隔がほとんど変わらず、いずれも1mmであった」とあるので、4つ目の印以降は、根の細胞の縦方向の長さは伸びていないことが分かります。
問われているのは、印をつけたときの根の先端からの距離の範囲です。
1つ目の印をつけた部分は「図2」より、根の先端からの距離が1mmにあり、4つ目の印をつけた部分は「図2」より、根の先端からの距離が4mmにあるので、
よく伸びた部分である1つ目から4つ目の印をつけたときの根の先端からの距離の範囲は、1mm〜4mmとなります。
なお、根の先端からの距離が1mmまでは根冠で細胞は成長しませんが、1mm〜4mmには、根の成長点(根端分裂組織)があるので、細胞が作られ、成長点より上のところで成長して根が伸びます。
②
問われているのは、「根の細胞が縦方向に伸びた」「根の先端からの距離」の範囲です。
実験1の「図3」の根Bは、根の細胞の縦方向の長さ調べるためにあり、根の先端からの距離(mm)と、細胞の縦方向の長さ(mm)との関係を表したグラフが「図5」です。
「図5」を見ると、根の細胞が縦方向に伸びたのは、根の先端からの距離が1mm〜8mmであることが分かります。
7〜8mmの範囲でも根の細胞は縦方向に伸びているので、1mm〜7mmは誤りです。
なお根冠がある0〜1mmの範囲ですが、実験[2]の問題文に「1つ目の印の位置はほとんど変わらなかった」とあるので、この範囲の根の細胞は縦方向に伸びていないことが分かります。
③
まず問題文を読むと「これらのことから」とあるので、問題①と②のデータを使用します。
問題文に、「根の先端からの距離が「③」の範囲にあった細胞の縦方向ののびは」とあるので、
根の細胞が縦方向にのびた、根の先端からの距離が1mm〜8mmのデータを使用することが分かります。
問題①より、根の細胞が縦方向によく伸びた部分は、根の先端からの距離が1mm〜4mmなので、
根の先端からの距離が4mm〜8mmにあった根の細胞の縦方向ののびは、1mm〜4mmにあった根の細胞の縦方向ののびと比較して、根の伸びへの影響は無視できるほど小さいといえます。


