👉教師紹介・料金
※授業料1回1,500円+交通費(コミコミ最大3,000円)・入会金なし・お好きな日時に受講・3回のお試し期間あり(無料教材あり)
■総合ABC範囲表
>>【最新版】総合ABC範囲表
■総合A過去問
科目別:国語、数学、社会、理科、英語
年度別:2024年、2023年、2022年、2021年、2020年、2019年、2018年、2017年、2016年
■総合B過去問
科目別:国語、数学、社会、理科、英語
年度別:2024年、2023年、2022年、2021年、2020年、2019年、2018年、2017年、2016年、2015年
■総合C過去問
科目別:国語、数学、社会、理科、英語
年度別:2024年、2023年、2022年、2021年、2020年、2019年、2018年、2017年、2016年、2015年
■総合ABC道コン偏差値
>>総合ABC道コン偏差値(SS)推移
☆学力テストはこれで完璧!オリジナル教材☆
👉北海道学力テストはこれで完璧!オリジナル教材+過去問一覧
※過去問の販売はできませんのでご注意ください。
中学3年北海道学力テスト総合C「数学」(2019)の平均点と難易度
私が指導している生徒さんの話をまとめると、今回の総合Cの数学の平均点は25〜30点ほどだったみたいです。
私が実際に問題を見た感想ですが、「やや難」と感じました。
2019年の総合Bよりも、遙かに難しいです。
2019年の総合Aと比較すると、今回の数学はやや難しいと感じました。
今回の総合Cは、本番の入試数学の標準問題のレベルを超えています。
が、学校裁量問題よりは易しいです。
今回の総合Cは、学校のワークを「ある程度分かる」レベルだと、36点(6割)がやっと、しっかりやっていて、48点(8割)が狙えた感じです。
が、『塾技 数学100』の例題レベルを理解した上で暗記している子なら、満点が狙えるでしょう。
中〜上位の公立高の受験生は、本番で難しい学校裁量問題を解かねばなりません。
手稲・新川以上を狙うなら、学校裁量問題の易しめの問題は落とせません。
学校裁量問題は、易しめの問題でも総合ABCより遙かに難しいです。
総合ABCで点数が微妙だった子は、危機感を持ち受験生になりましょう。
数学は暗記科目です。
『塾技 数学100』の例題レベルを「理解した上で暗記」していれば、学校裁量問題でも時間内に解けますので、残り4ヵ月間ガマンして勉強してください。
点数が取れるかどうかは、頭の良し悪しではなく、どれだけガマンしたかで決まります。
(そのガマンの度合いも、部活と比べたら大したことないです)
中学3年北海道学力テスト総合C「数学」(2019)問題・解答・解説
次に、中学3年北海道学力テスト総合Cの「数学」の問題・解答・解説を紹介します。
大問1 小問集合
問1

易しい計算問題ですが、ケアレスミスを防ぐため、工夫して計算するよう心がけましょう。
(3)は√3で通分すると、分母が整数になりますが、
今回はそれをやらなくても簡単に解けそうなのでやりませんでした。
以下、解答です。
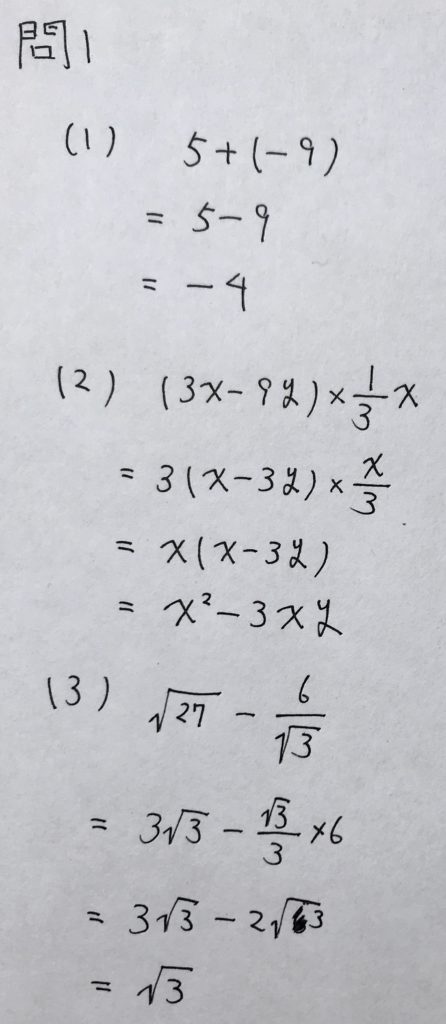
問2
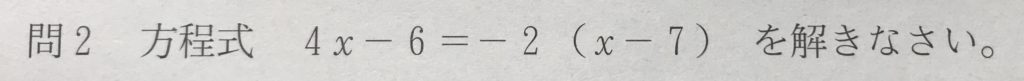
学校のワークのBレベル(標準レベル)の問題です。
右辺を展開して流れ作業で計算すればOKでしょう。
左辺が2で割れることに着目して、式を簡単にするのもありです。
以下、解答です。
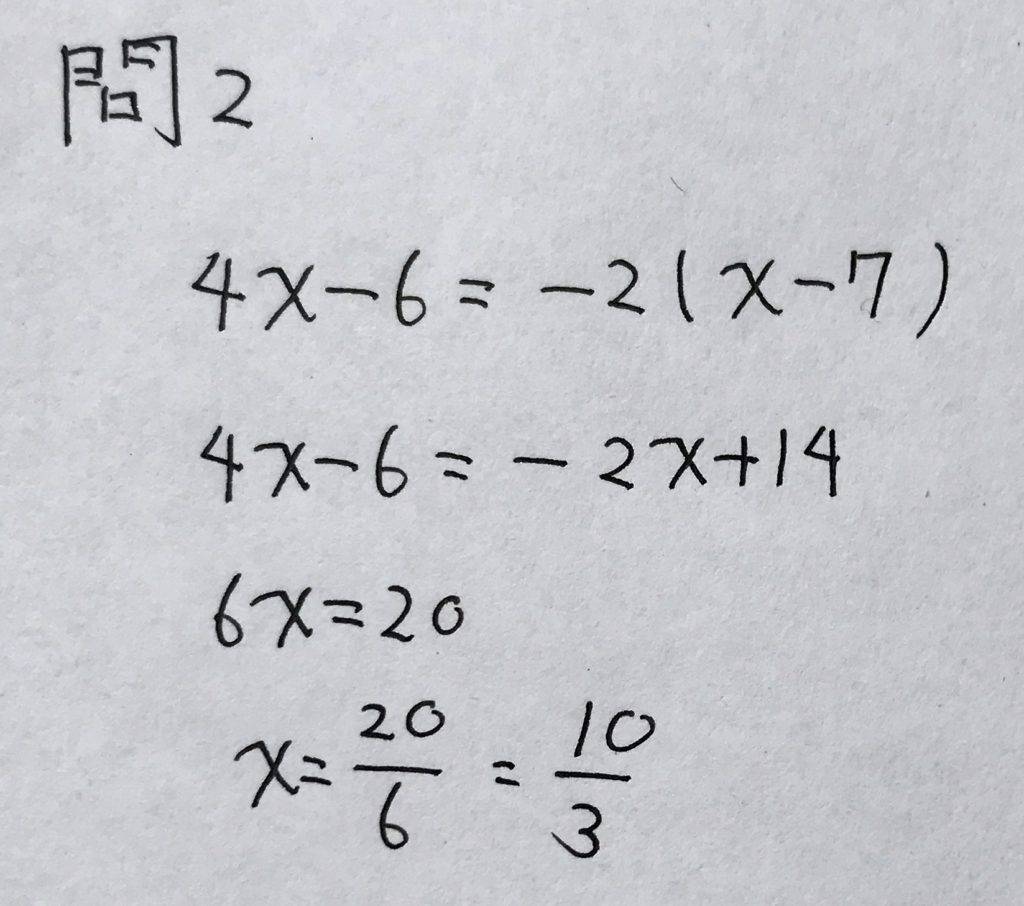
問3
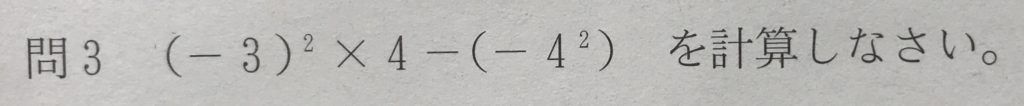
学校のワークのBレベル(標準レベル)の問題です。
ぱっと見、「a2-b2=(a-b)(a+b)」のかたちにして計算するのかなと思いましたが、
この問題は流れ作業で解くだけでした。
以下、解答です。
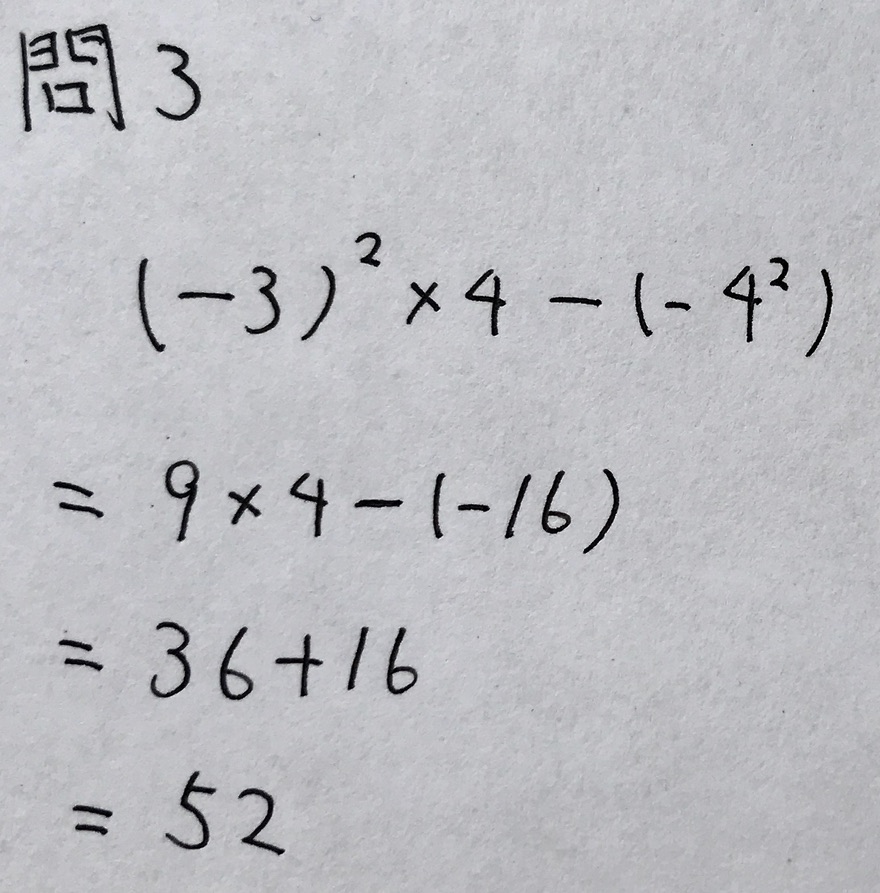
問4

学校のワークのBレベル(標準レベル)〜Cレベル(やや難しい)の問題です。
xの増加量とyの増加量が与えられているので、変化の割合=傾きで処理するのは分かるでしょう。
二次関数なので変化の割合の公式が使えます。
しかし、変化の割合の公式を理解せずに暗記しているだけだと、この問題は解けなかったかもしれません。
以下、解答です。

問5

学校のワークのBレベル(標準レベル)の問題です。
代表的な相似形として、6種類の図形を暗記する必要があります。
北海道公立高校入試数学の相似な図形の問題は、証明問題を含めて、6種類の図形のかたちと証明内容を理解した上で暗記していれば、ほぼ確実に解けます。
代表的な相似形は『塾技 数学100』に書かれています。
以下、解答です。
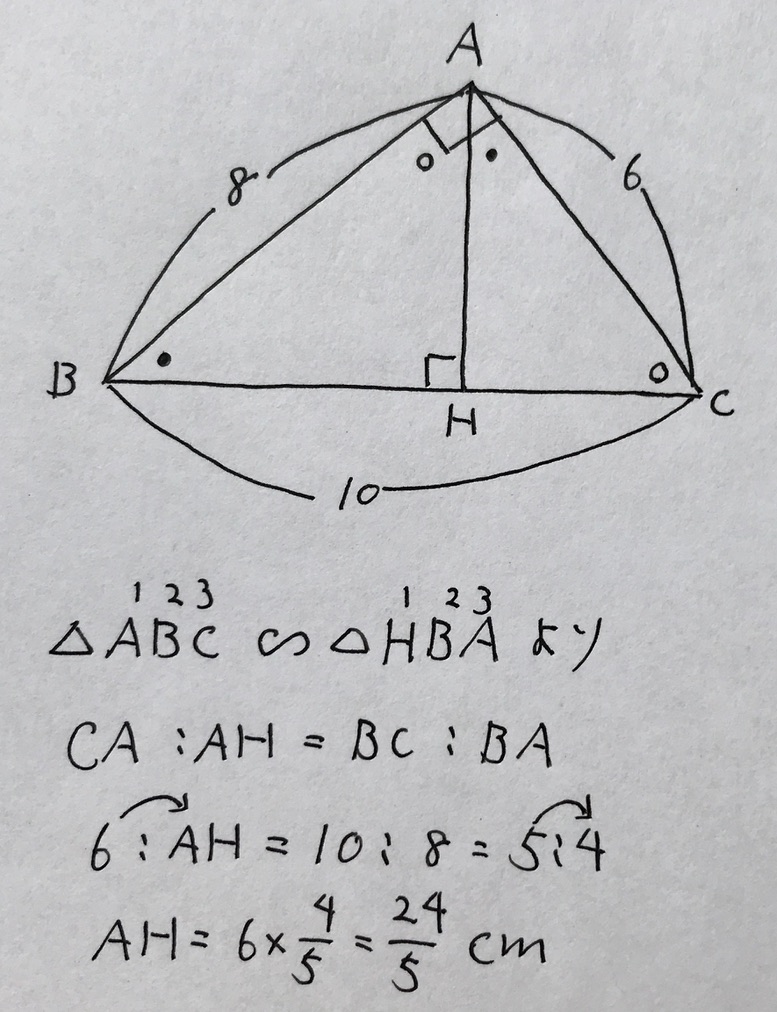
相似な図形→対応する辺で比例式を立てる、の流れで解くことができますが、
これから習う3辺比の知識を使うと、もっと簡単に解けます。
以下、別解です。
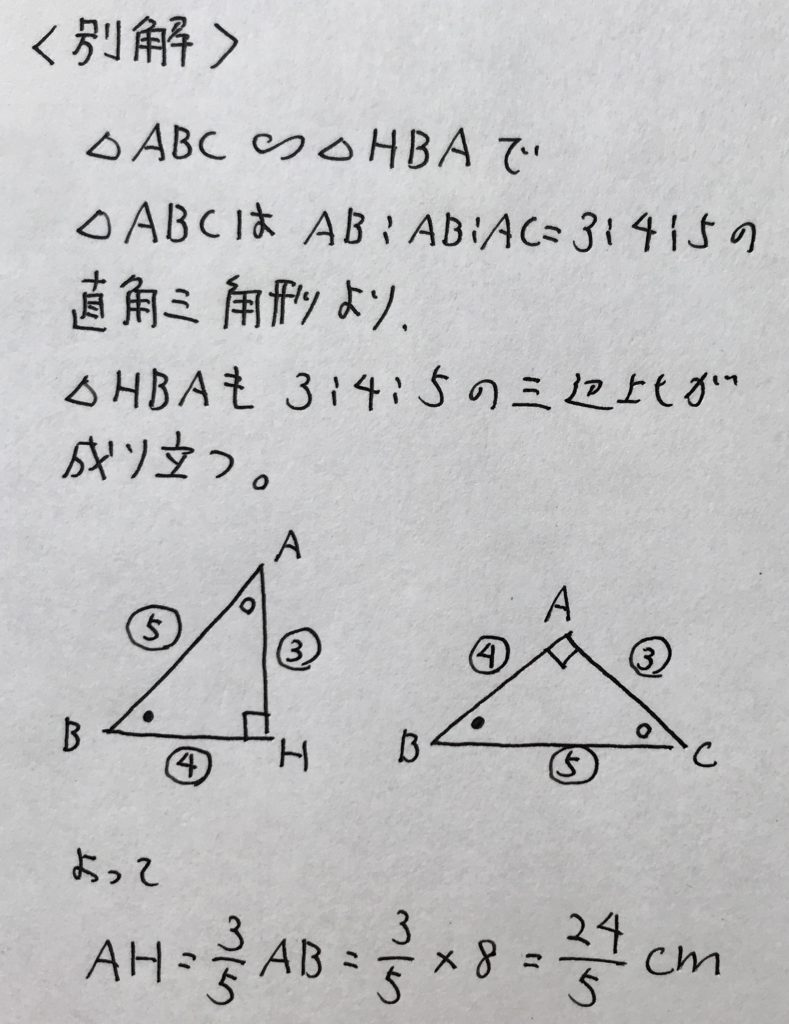
大問2 小問集合
問1
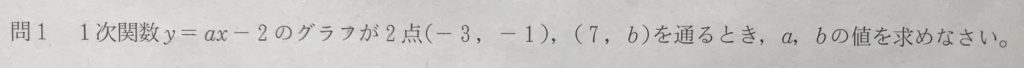
学校のワークのBレベル(標準レベル)の問題です。
流れ作業で計算するだけです。
以下、解答です。
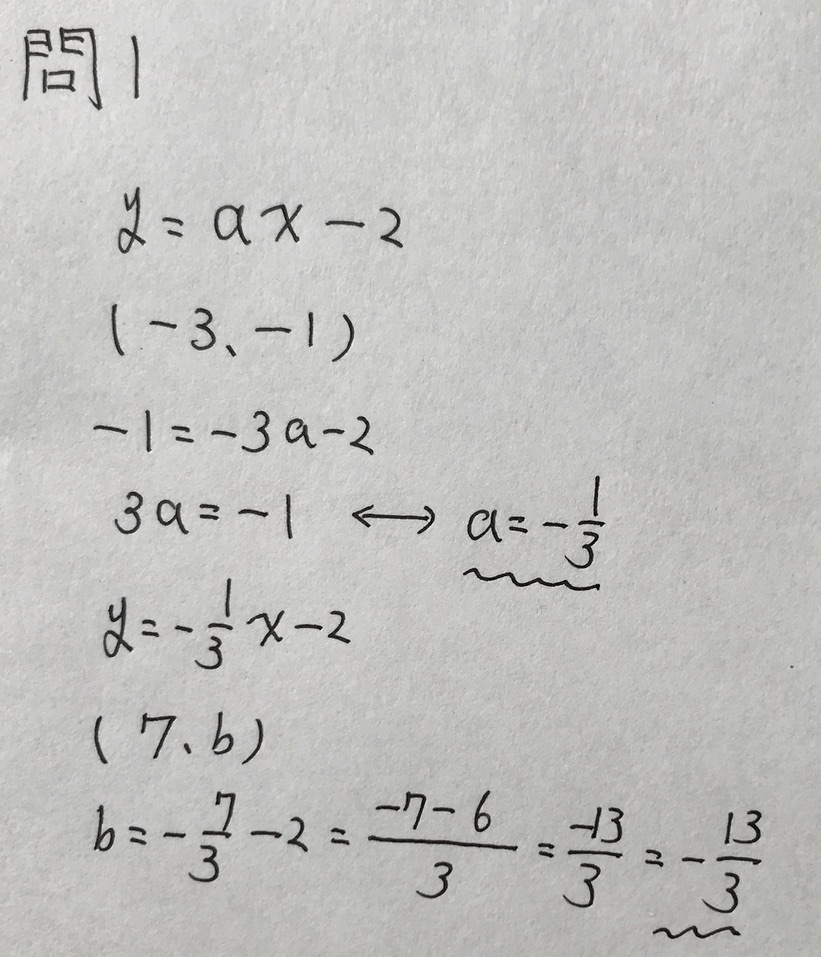
問2(やや難)

学校のワークのCレベル(やや難しい)の問題です。
10以上の5つの素数は、11、13、17、19、23であることは、書き出せばすぐに分かります。
しかし、求める整数は23より大きい整数で、かつ最小の整数であることから24になります。
このように書き出せば何とか解けるのですが、それだと本番対応力は高いと言えません。
以下の解答例のように解くようにしましょう。
以下、解答です。

問3
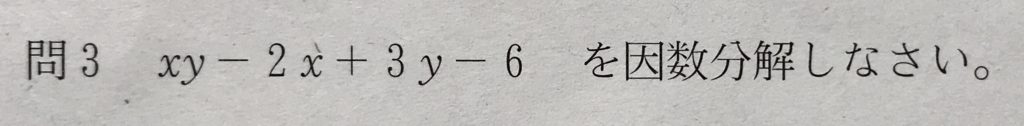
学校のワークのBレベル(標準レベル)の問題です。
4項式の因数分解の問題です。
北海道公立高校入試数学では、2項式か3項式の因数分解の問題が出題されます。
4項式、5項式、6項式の因数分解の問題は、難関私立でよく出題されます。
公立高校入試の本番では4項式以上の因数分解の問題は出ないでしょうが、万が一ということもありますので、上位高狙いの子は抑えておきましょう。
4項式、5項式、6項式の因数分解の問題は解き方が決まっており、『塾技 数学100』に詳しく書かれています。
以下、解答です。

問4

学校のワークのBレベル(標準レベル)の問題です。
流れ作業で計算するだけです。
以下、解答です。
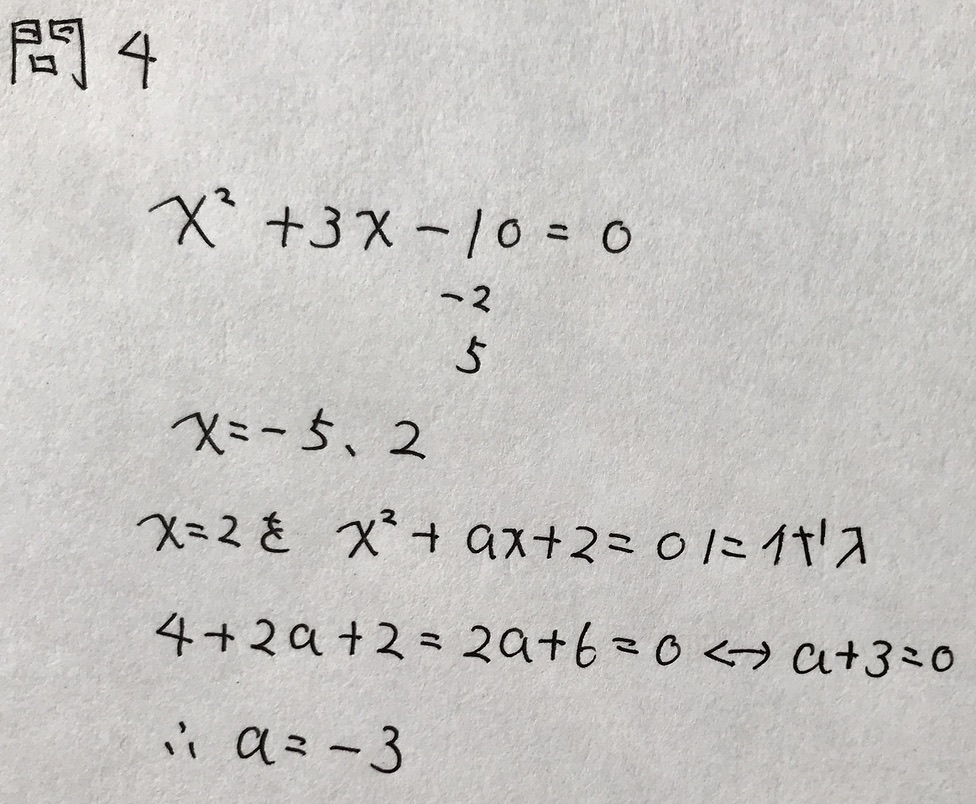
問5(やや難)
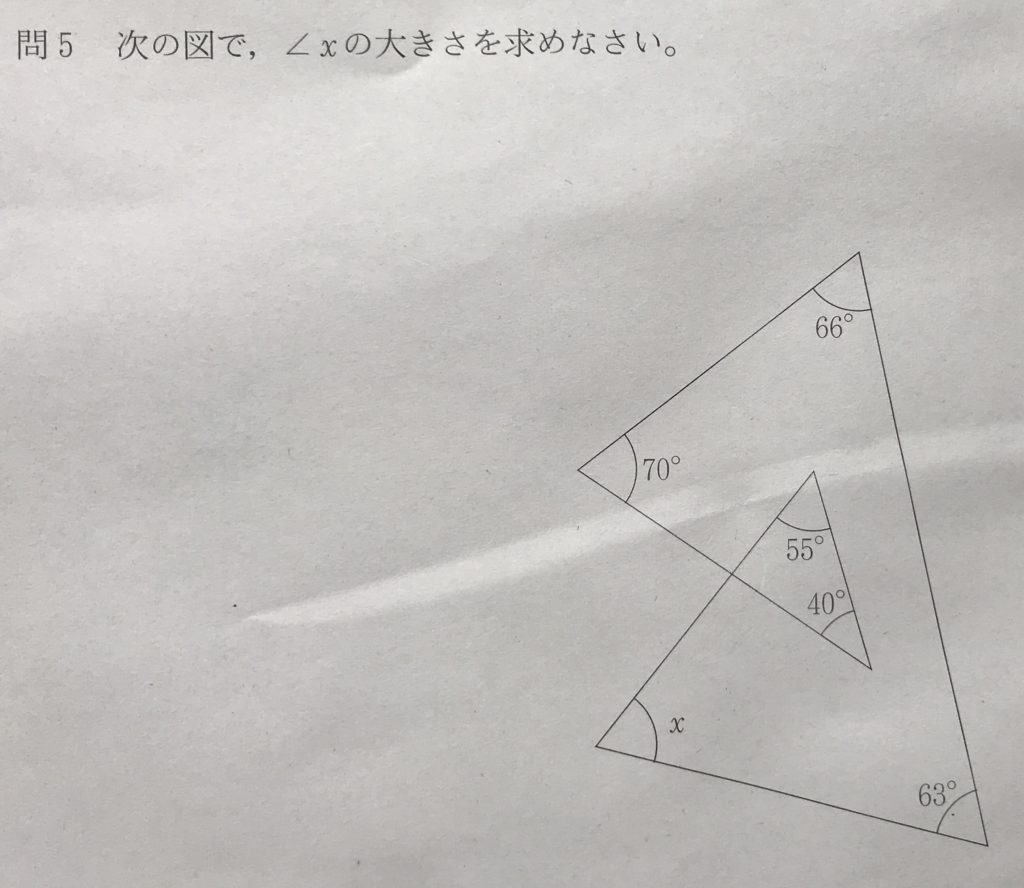
学校のワークのCレベル(やや難しい)〜Dレベル(難しい)の問題です。
この図形を5角形と見て、内角の和=540°で方程式を立式してもよいでしょう。
しかし、補助線を引いて4角形と見て、内角の和=360°で方程式を立式すると、より簡単になります。
この場合、不明な角度が2つ追加されてしまいますが、内角の和で立式する際に数値化できます。
以下、解答です。

大問3 小問集合
問1(やや難)

学校のワークのCレベル(やや難しい)の問題です。
√の大小比較は2乗して考えます。
ここまでは、多くの生徒さんが知っている知識でしょう。
しかしこの問題の場合、2乗したあと手が止まった子が多かったのではないでしょうか。
この問題は「具体化」して解きます。
『2018年の総合C数学』では、この問題よりさらに難しい問題が出題されました。
以下、解答です。

自然数の不等式の範囲を利用して、以下のように解くこともできます。
以下、別解です。

問2

学校のワークのAレベル(易しい)〜Bレベル(標準レベル)の問題です。
中1で習う、「〜%増し」「〜%引き(減)」「〜割増し」「〜割引き(減)」の知識が必要ですが、
それを知っていれば、この問題は難なく解けるでしょう。
以下、解答です。
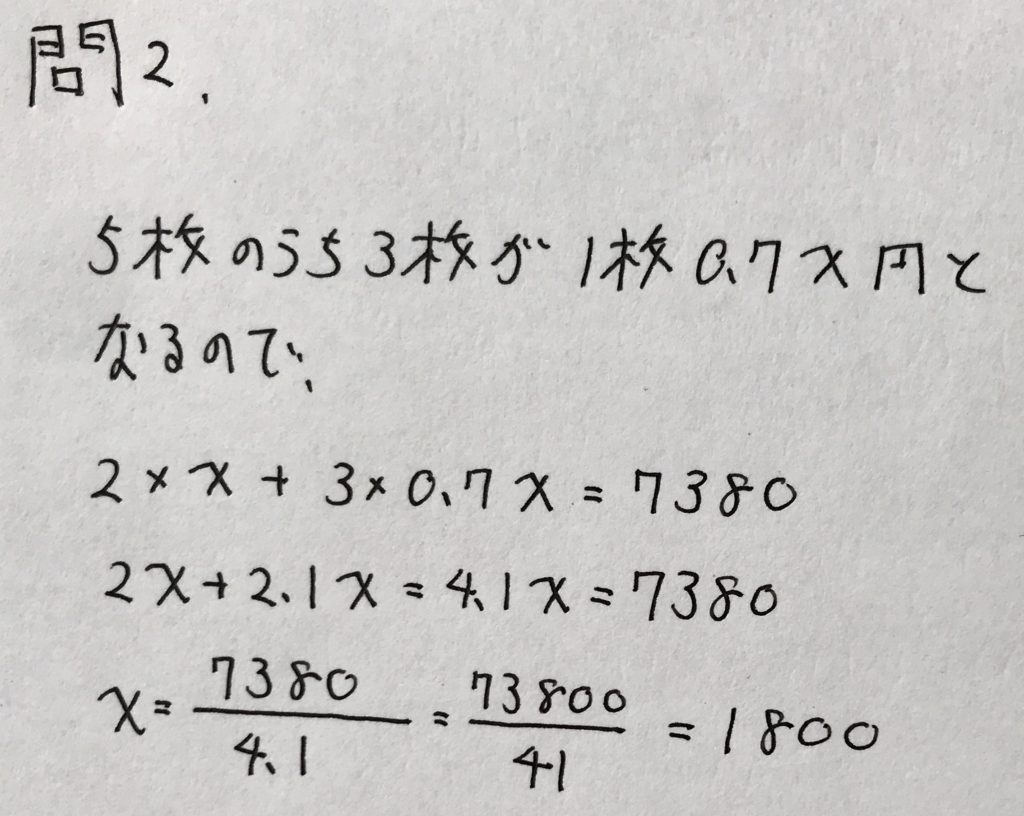
問3(やや難)

学校のワークのCレベル(やや難しい)〜Dレベル(難しい)の問題です。
この問題は、暗算力と地道に数えあげる集中力が要求される問題です。
以下、解答です。

ところで、与えられた式の分母のa+bは156を割り切れる数なので、「約数の問題かな?」と思えます。
A=XaYbZc(X、Y、Zは素数)のとき、Aの約数の個数は(a+1)(b+1)(c+1)となります。
これを利用すると一応答えが出せますが、誤りです。
以下、誤った解答です。

この解答が誤っている理由は、以下のとおりです。
===========
・約数の個数の式は1を加味しているが、サイコロの目の和a+bは2以上の整数である
・確率の分母は6×6=36だが、これは2つのサイコロの目の並び順を区別した順列である。しかし約数の個数の式は素数の組み合わせであり並び順を区別していない。確率を求めるとき、順列か組み合わせで統一しなければならないので、約数の個数の式を用いることはできない。
===========
約数の個数の式は、難関私立の入試で高得点を取るなら、必須の知識です。
しかし、約数の個数の式をきちんと理解していないと、このような問題が出題されると間違えます。
大問4 図形問題(やや難)
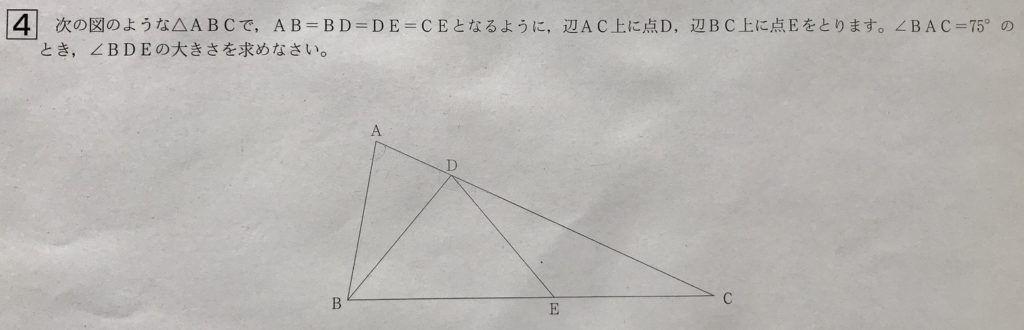
学校のワークのCレベル(やや難しい)の問題です。
よくあるパターンの問題です。
このタイプの図形問題は、外角の性質を用いれば解けます。
しかし、∠DBEの外角を求めるとき、対頂角が混ざってくるところにひとひねりあります。
以下、解答です。

大問5 二次関数

問1
学校のワークのAレベル(易しい)の問題です。
以下、解答です。
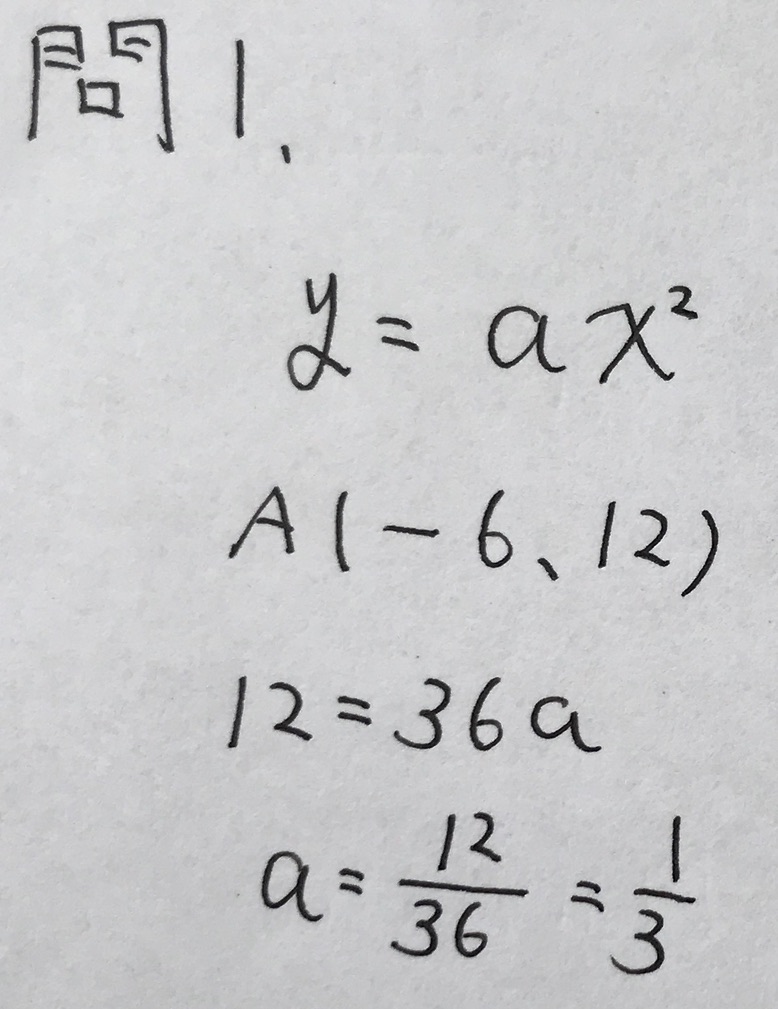
問2(難)
学校のワークのDレベル(難しい)の問題です。
学校裁量問題の難しめの問題に相当するレベルの問題です。
以下の思考プロセスで解いていきます。

ところで、□ABOCは台形になることが分かりますでしょうか。
直線OBの傾きは-1、直線OCの傾きは1で、傾きどうしの積が-1となるので、直線OBとOCは直交します。
また、直線ACの傾きは-1、直線OCの傾きは1で、傾きどうしの積が-1となるので、直線ACとOCは直交します。
線分OCとCAにおいて、∠BOC+∠OCA=180°で、同側内角の和=180°となるので、線分OCとCAは平行で、□ABOCは台形になります。
直線が台形の上底と下底(上底と下底の頂点でもよい)を通る場合、
この直線が上底の中点と下底の中点を結んだ線分の中点を通るとき、直線は台形の面積を2等分します。
が、直線CPは下底ACの頂点を通りますが、上底OBを通らないので、残念ながら台形の面積を2等分する知識は使えません。
台形の面積を2等分するパターンの問題は、難関私立でよく出題されるので、ここで抑えておきましょう。
大問6 図形問題
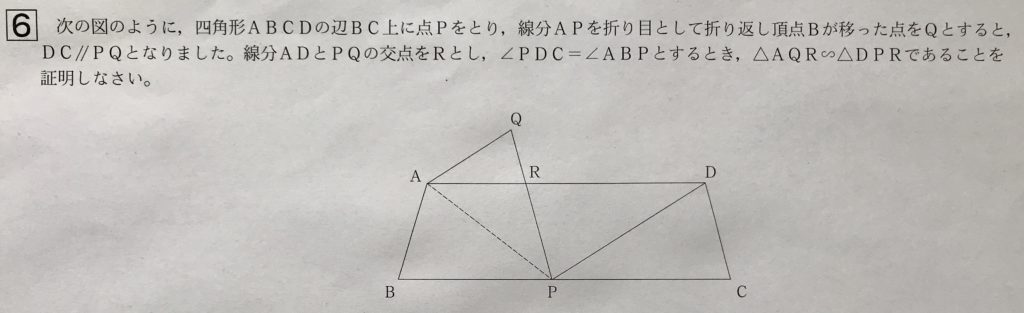
学校のワークのBレベル(標準レベル)の問題です。
相似な図形で習う折り返しの問題の知識と、平行線の性質(錯角と同位角が等しい)の知識があれば、難なく解けます。
以下、解答です。
