【2019年過去問】中学3年北海道学力テスト総合B「数学」の問題・解答（答え）・詳しい解説を公開！

 

☆過去問ダウンロードはこちら☆

👉北海道学力テスト過去問ダウンロード

※生徒以外で過去問のみをお求めの方は、こちらにご連絡ください（過去問の「原本」を頂ける方は歓迎します！）。
👉お問い合わせ

中学3年北海道学力テスト総合B「数学」（2019）の平均点と難易度

私が指導している生徒さんの話をまとめると、今回の総合Bの数学の平均点は25点ほどだったみたいです。

 

私が実際に問題を見た感想ですが、「易」と感じました。

 

前回の総合Aよりも、明らかに易しいです。

＞＞2019年総合Aの問題と解説

 

今回の総合Bは、学校のワークが「ある程度分かる」レベルでも、7割以上は取れたはずです。

 

『塾技 数学100』の例題レベルを暗記している子なら、満点をあっさりと取れたでしょう。

 

今回の総合Bで高得点が取れた子は、慢心せずに典型問題の理解した上での暗記を続けて下さい。

 

点数が微妙だった子は、危機感を持ち受験生になりましょうね。

中学3年北海道学力テスト総合B「数学」（2019）問題・解答・解説

次に、中学3年北海道学力テスト総合Bの「数学」の問題・解答・解説を紹介します。

大問1　小問集合

問1

 

 

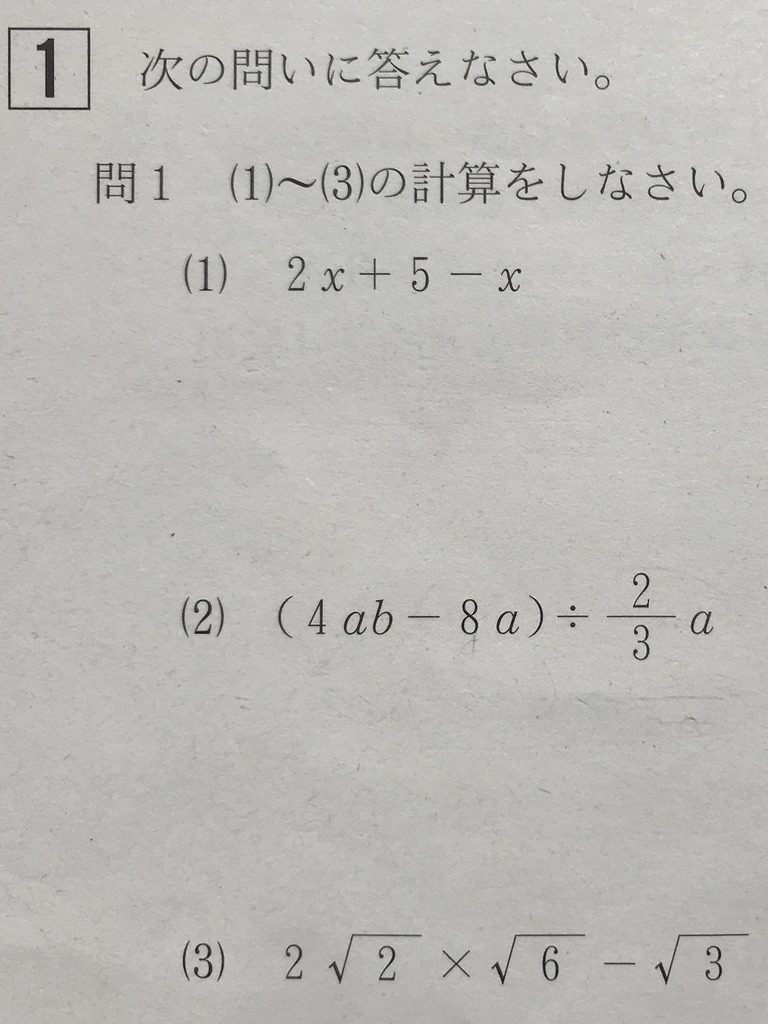
力業でもよいのですが、入試本番の精神状態を鑑みると、工夫して計算したほうが間違えないでしょう。

 

本問は、因数分解してから計算するとよいかと。

 

以下、解答です。

 

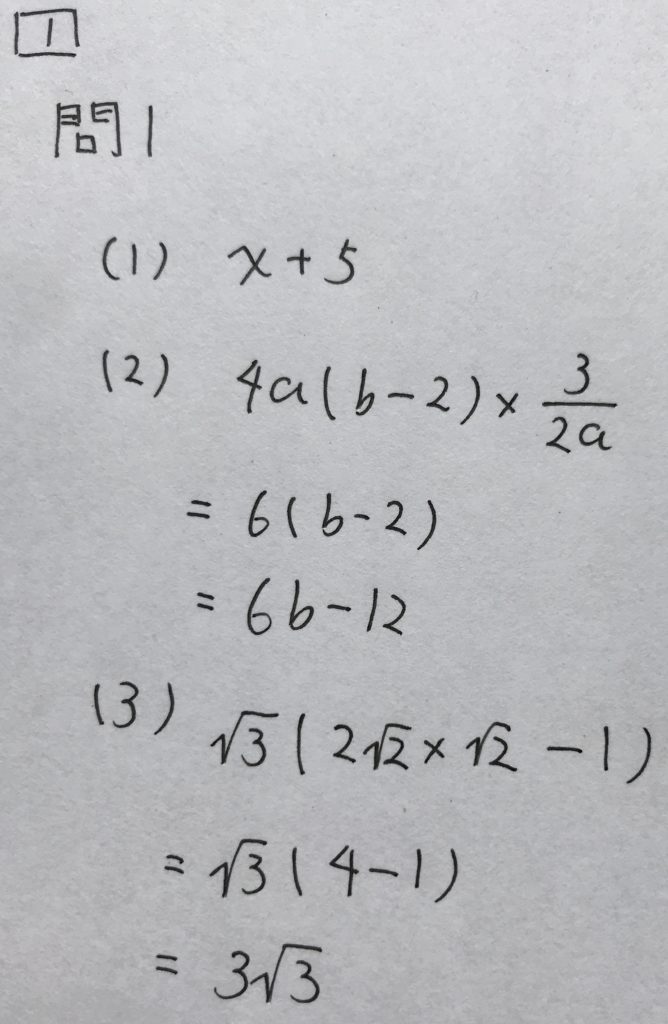
問2

 

 

学校のワークの易しめのレベルの問題です。

 

反比例の一般式は、「y＝a/x」で、「a＝x×y」と表すことができます。

 

反比例のグラフ（双曲線）の任意の点A（x,y）において、長方形の面積は比例定数になることも抑えましょう。

 

以下、解答です。

 

問3

 

 

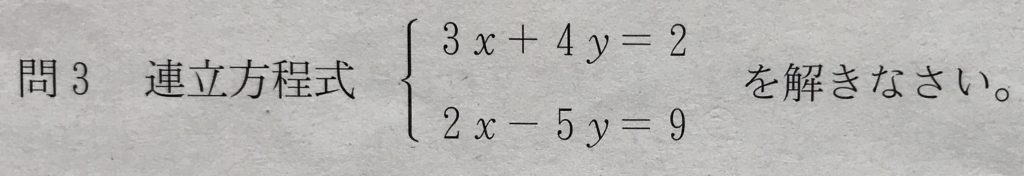
学校のワークの易しめのレベルの問題です。

 

二つの二元一次方程式のyの係数の符号が逆になっているので、yを消去してxの値を求め、yの値を求めます。

 

以下、解答です。

 

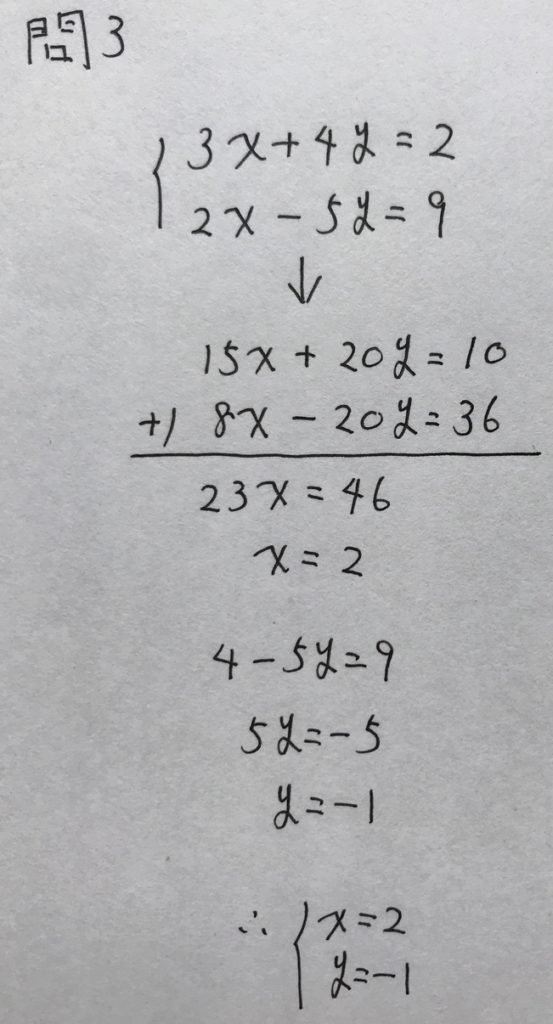
問4

 

 

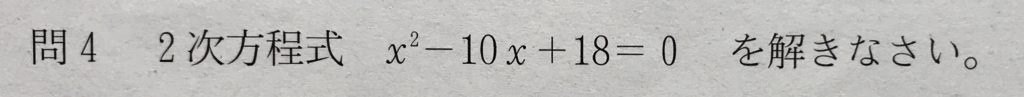
学校のワークの易しめのレベルの問題です。

 

左辺は因数分解ができないので、解の公式を用います。

解の公式は2パターンあるので、ここで解答例で紹介します。

 

因数分解ができない二次方程式は、平方完成を用いて解くこともできます。

 

以下、解答です。

 

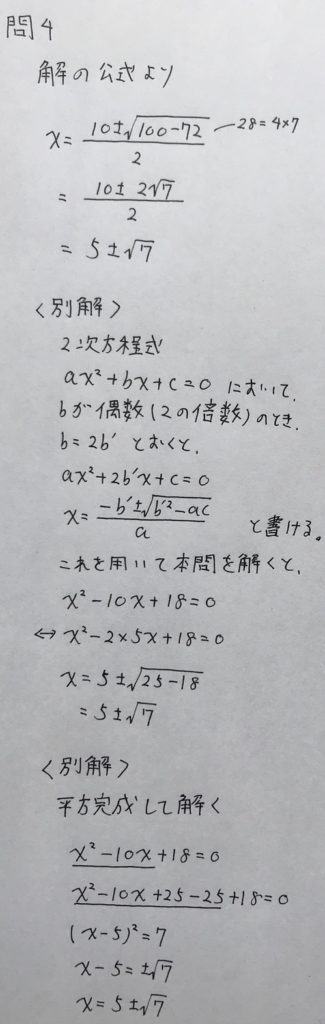
問5

 

 

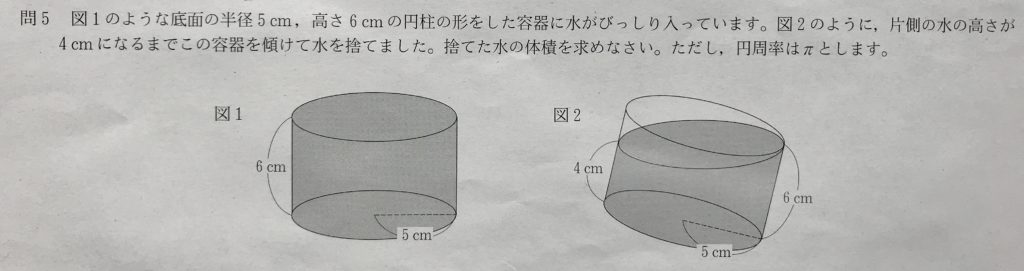
学校のワークの難しめのレベルの問題です。

 

捨てた水の体積は、図2の空白部分です。

この部分の体積は、半径5cm、高さ2cmの円柱の半分であることに気づくことができれば、解けます。

 

以下、解答です。

 

大問2　小問集合

問1

 

 

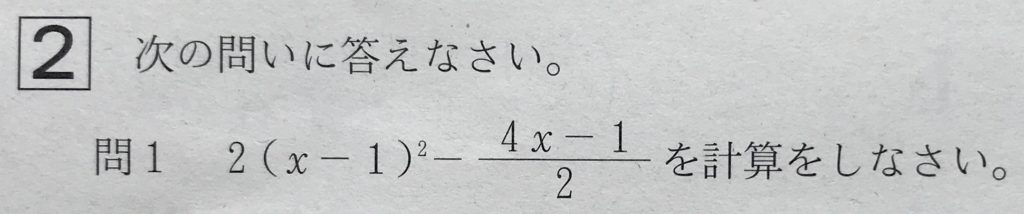
学校のワークの標準レベルの問題です。

 

工夫して計算できなそうなので、力業で計算していきます。

 

以下、解答です。

 

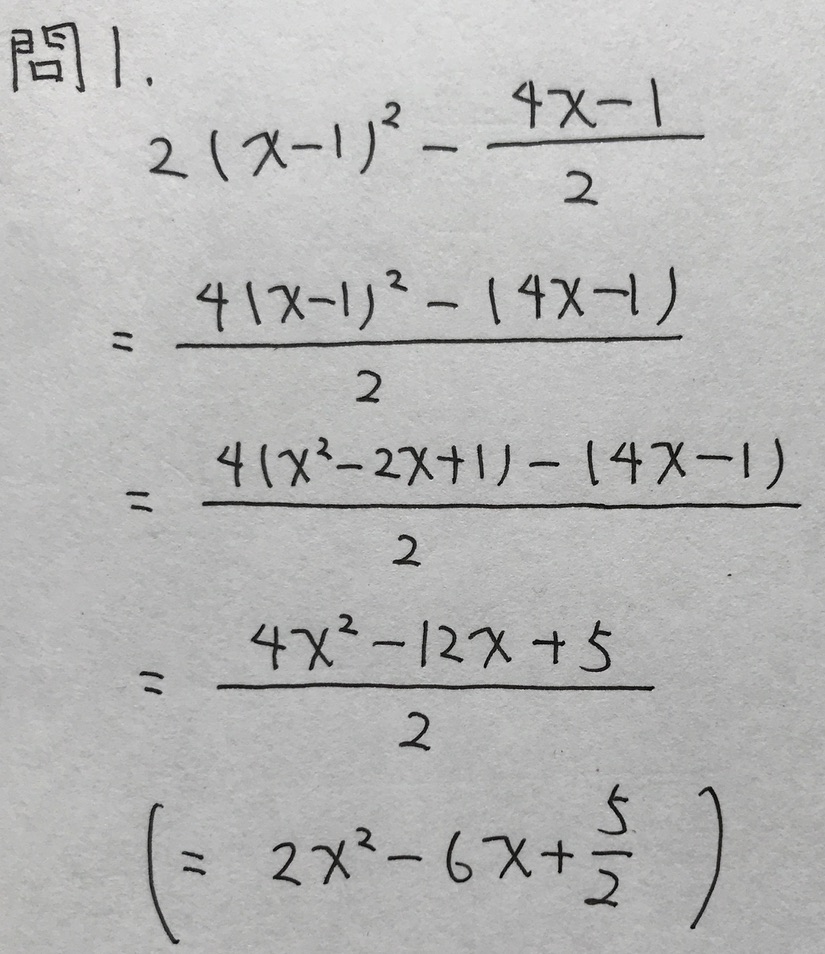
問2

 

 

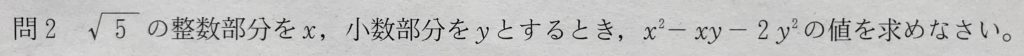
学校のワークの標準レベルの問題です。

 

√5の整数部分と小数部分を求めるのは、簡単でしょう。

 

しかし、求値式が対称式でないので、和と積のかたちにできません。

 

ここは、求値式に値を代入して、力業で計算していきます。

 

以下、解答です。

 

問3

 

 

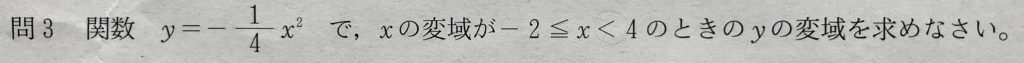
学校のワークの易しめのレベルの問題です。

 

xが0をまたぐので、二次関数の変域の公式を用いて一発で解けます。

 

xが絶対値の最大値である4を含まないことに注意が必要です。

 

以下、解答です。

 

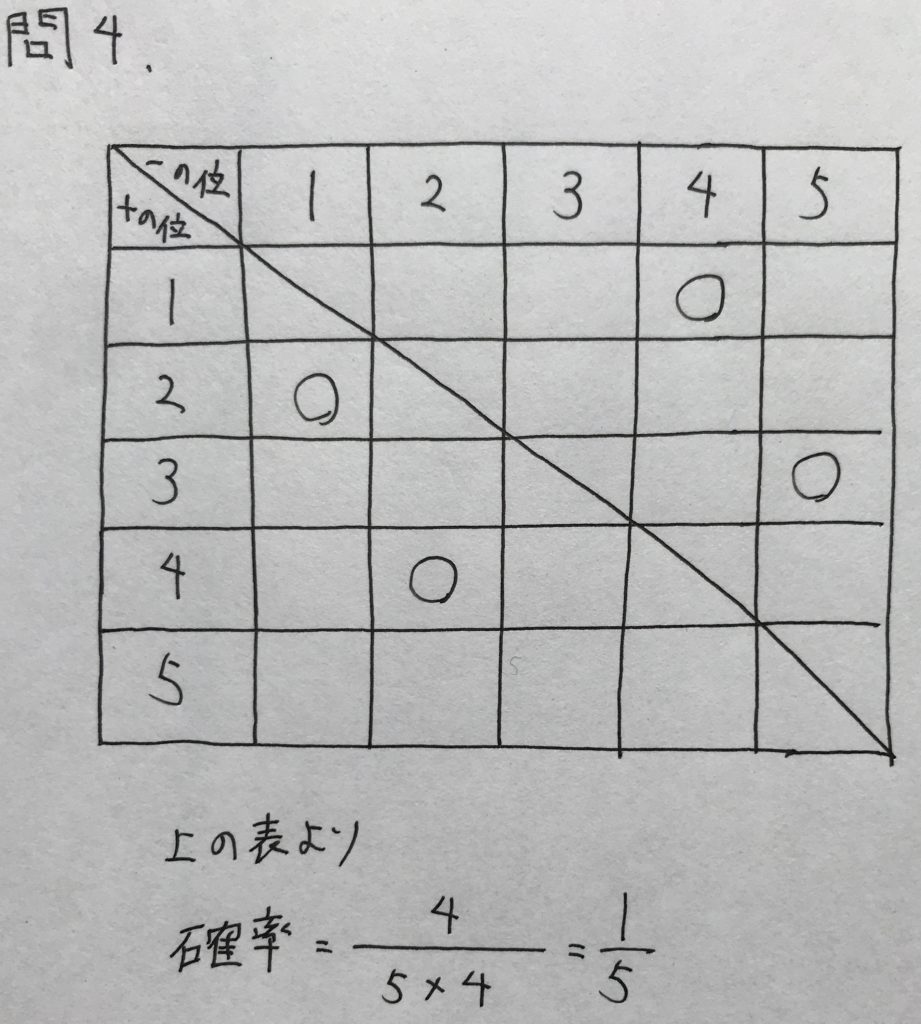
問4

 

 

学校のワークの易しめのレベルの問題です。

 

樹形図ではなく、マトリックスを書けば速攻で解けます。

 

以下、解答です。

 

問5

 

 

学校のワークの難しめのレベルの問題です。

 

組み合わせの問題です。

2018年の夏の中3道コン数学で、類題が出題されています。

 

この問題は組み合わせの公式を使えば簡単に解けますが、知らないとかなり苦戦するでしょう。

 

ここでは、組み合わせの公式を用いて解きます。

 

以下、解答です。

 

大問3　小問集合

問1

 

 

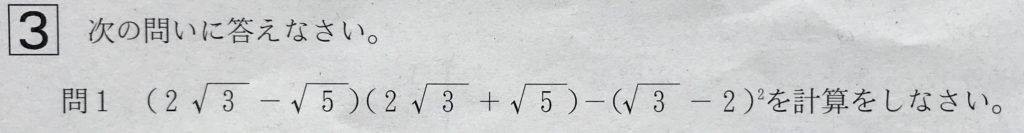
学校のワークの標準レベルの問題です。

 

中3の最初で習う、乗法公式を用いて解きます。

 

以下、解答です。

 

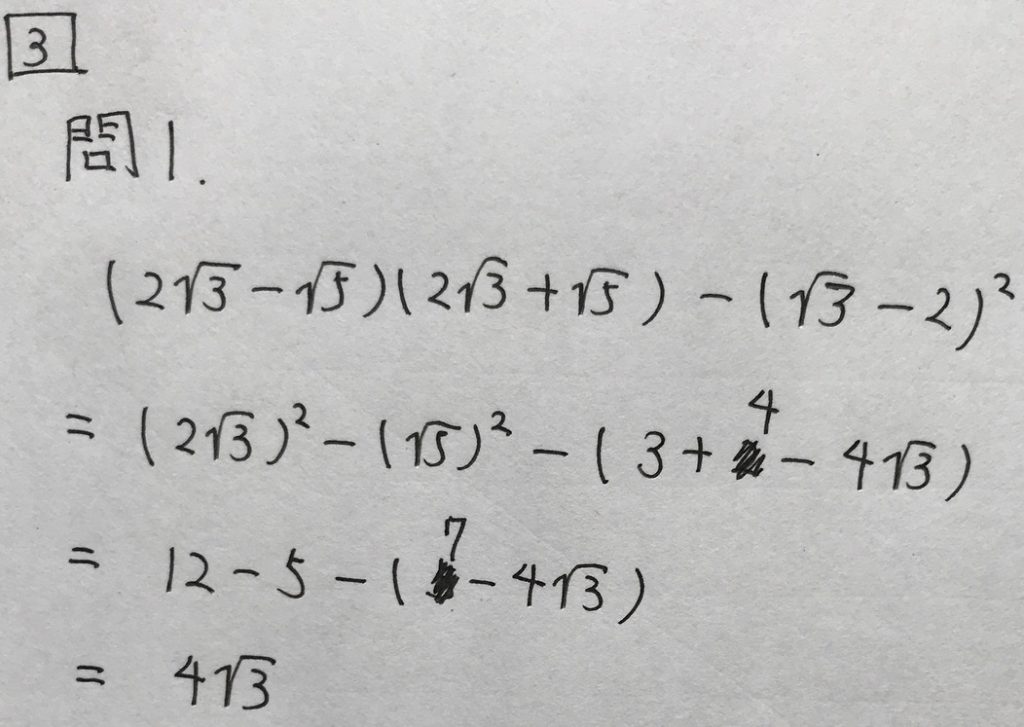
問2

 

 

学校のワークの標準レベルの問題です。

 

動点の問題ですが、点Pがカドを曲がらないので、ラクに解けます。

 

この問題は円の公式を知らないと解けないので、忘れた子は要復習です。

 

以下、解答です。

 

大問4　一次関数

問1

学校のワークの標準レベルの問題です。

 

△OACをy軸で回転させると、円錐ができます。

 

点Aと点Cの座標を求め、OAとOCの距離を計算し、錐体の体積の公式に代入して終わりです。

 

以下、解答です。

 

問2

学校のワークの標準レベルの問題です。

 

△OABも△OBDも、底辺と高さが容易に分かります。

 

△OABと△OBDの面積を計算し、△OABと△OBDの関係から方程式を立てて、点Dのx座標を求めます。

 

以下、解答です。

 

大問5　反比例（双曲線）

問1

学校のワークの標準レベルの問題です。

 

△OABも△OACも、底辺と高さが容易に分かります。

 

△OABと△OACの面積を計算し、△OABと△OACの関係から方程式を立てて、aの値を求めます。

 

以下、解答です。

 

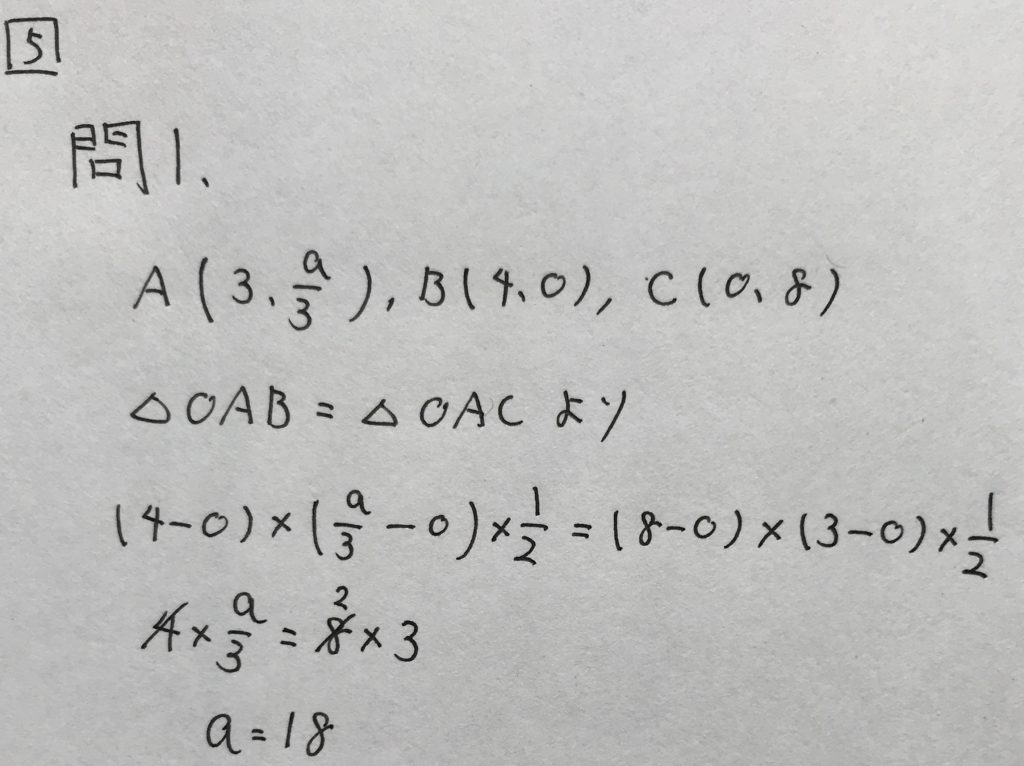
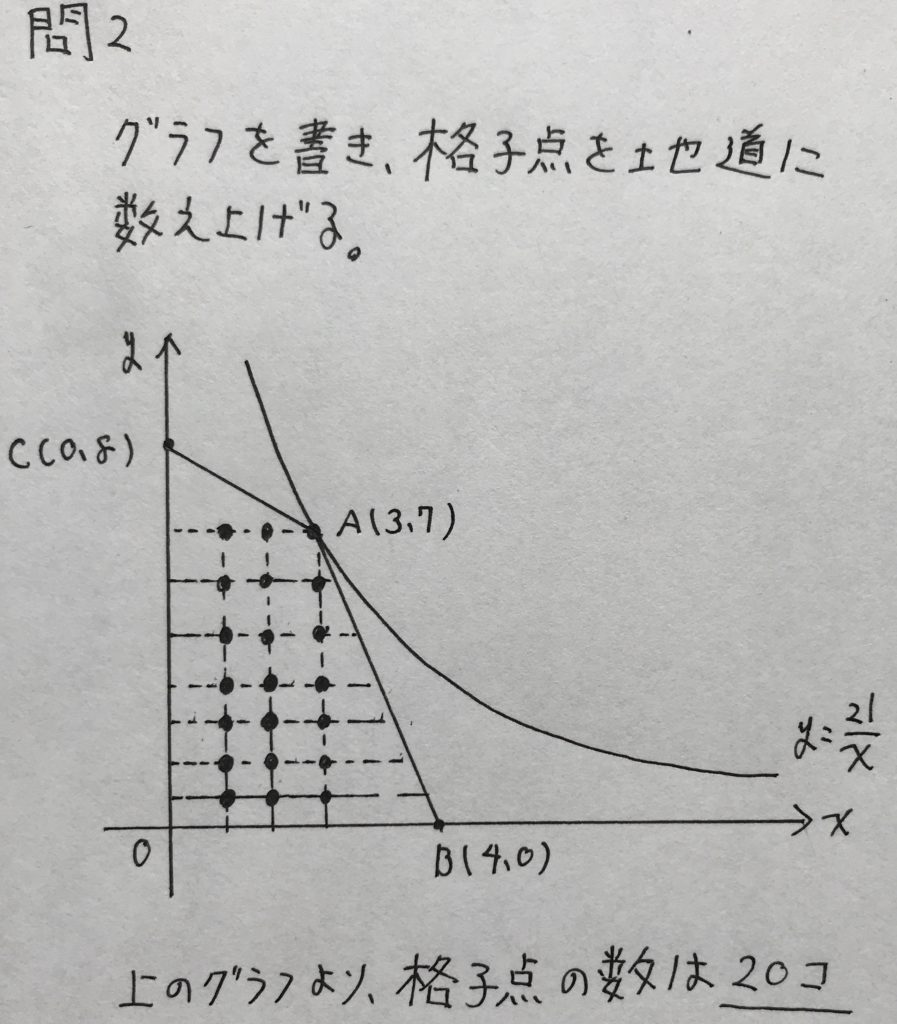
問2

学校のワークの標準レベルの問題です。

 

x座標とy座標がともに整数になる点を、格子点をいいます。

 

格子点を求める公式がありますが、本問は格子点を地道に数え上げる必要があります。

 

以下、解答です。

 

大問6　三角形の合同

 

 

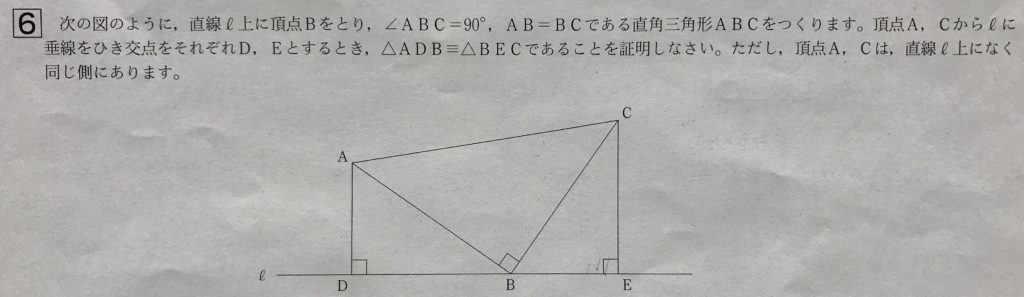
学校のワークの標準レベルの問題です。

 

相似な図形の学習を効率的に進めるために、角度を求めるとき、外角の性質を用いましょう。

 

以下、解答です。