こんにちは、個別指導塾まさです。
今回は、2019年9月11日（水）に行われた、中学3年北海道学力テスト総合Aの「数学」の問題・解答・詳しい解説を公開致します。
〜〜〜総合ABCの過去問と解説はこちら〜〜〜
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
＞＞【最新版】北海道の公立・私立高校受験対策おすすめ問題集（道コンSS・高校別）と差がつく正しい使い方
オンライン個別指導塾と家庭教師をやっています。北大院卒、指導経験20年以上。当塾は中上位高校志望の子が多いですが、勉強が苦手な子も多数在籍しています。今の学力は不問ですので、気軽にお申し込みください。授業料は1回70分 3,000円〜です。
＞＞教師紹介・料金・授業内容
＞＞体験授業かんたんお申し込み
＞＞お問い合わせ
中学3年北海道学力テスト総合A「数学」（2019）の平均点と難易度
私が指導している生徒さんの話をまとめると、今回の総合Aの数学の平均点は25点ほどだったみたいです。
私が実際に問題を見た感想ですが、「やや易」と感じました。
学校のワークが「ある程度分かる」レベルでも、42点（7割）以上は取れたはずです。
『塾技 数学100』の例題レベルを終わらせている子なら、満点をラクに取れるでしょう。
スポンサーリンク
中学3年北海道学力テスト総合A「数学」（2019）問題・解答・解説
次に、中学3年北海道学力テスト総合Aの「数学」の問題・解答・解説を紹介します。
大問1 小問集合
問1
ただ計算するだけです。
（3）は「割り算はかけ算（逆数）にする」のが鉄則です。
以下、解答です。
スポンサーリンク
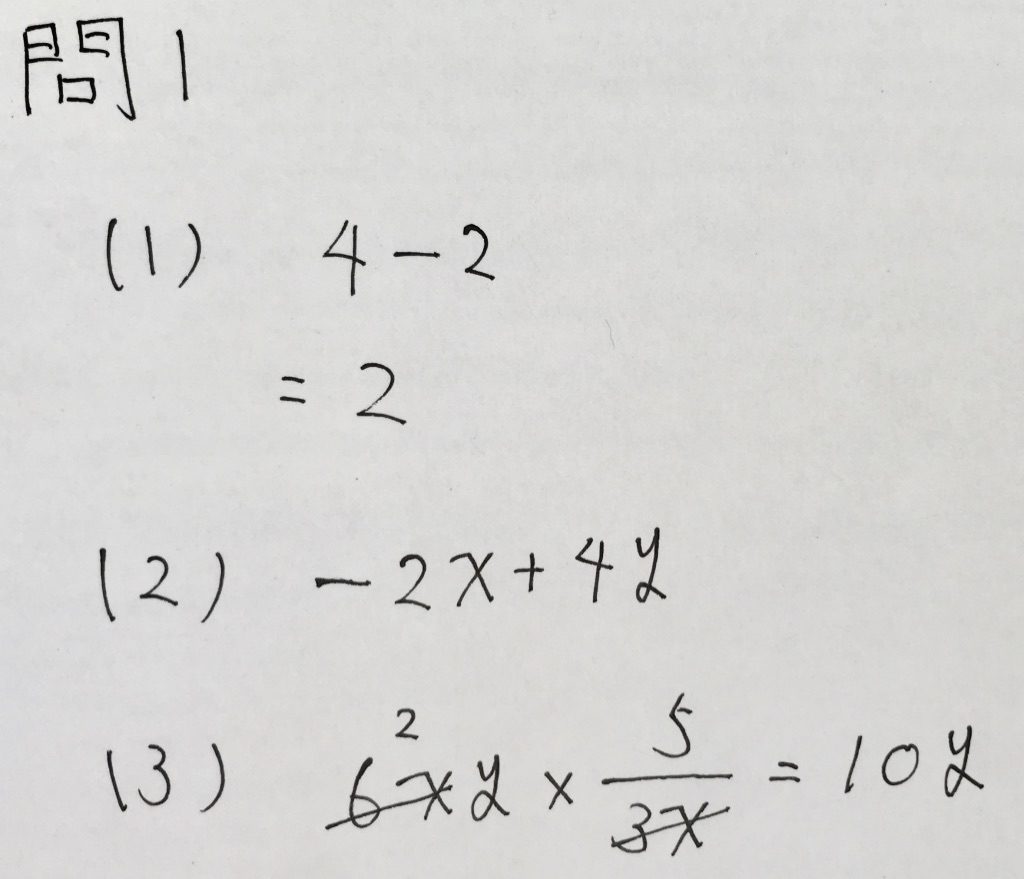
問2
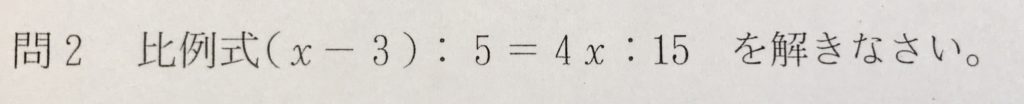
比例式の解き方として、ほとんどの受験生は「内内外外」を使うでしょう。
しかし、例えば
x：12＝3：4
x=12×3/4
と、右辺の比から等式を立てる方法もあります。
本番ではこちらを使いこなせないと高得点を取るのが難しいので、比を使いこなせるよう頑張ってください。
以下、解答です。
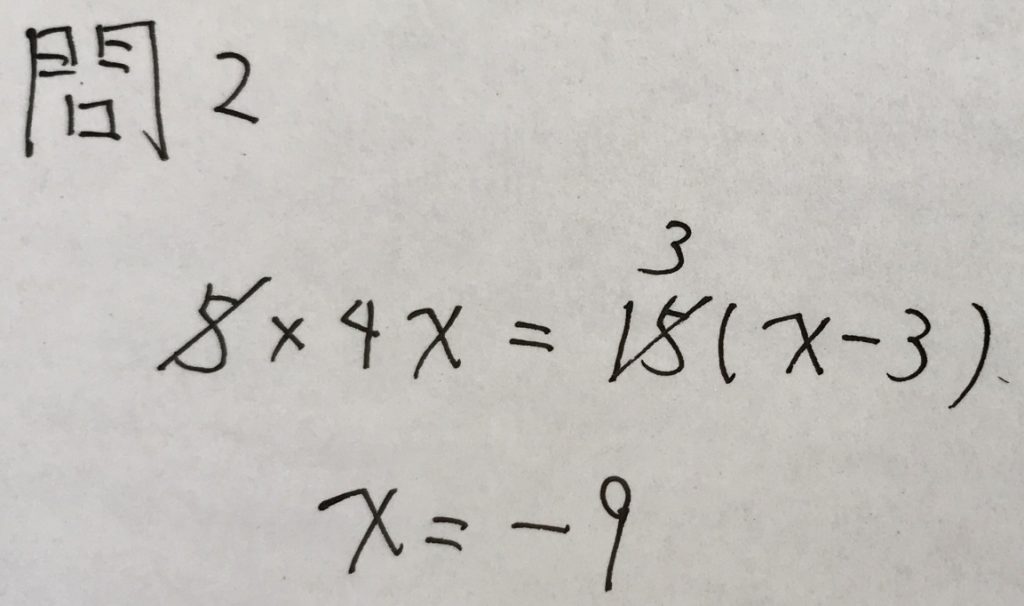
問3
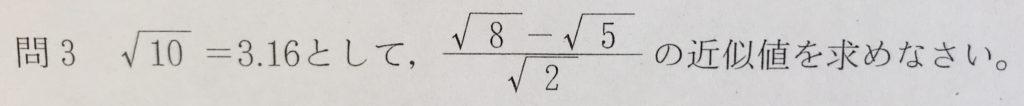
「多分分母の有理化を使うと、√10以外は整数になのだろう」と予測できればOKです。
分母の有理化を使うのはみんな分かるでしょうが、近似値という言葉にびびって解けなかった子が多かったのではないでしょうか。
分母の有理化では「分母は√が消え分子は分母の√が来る」ことを知っていると、
分母の有理化を暗算で出来るようになります。
以下、解答です。
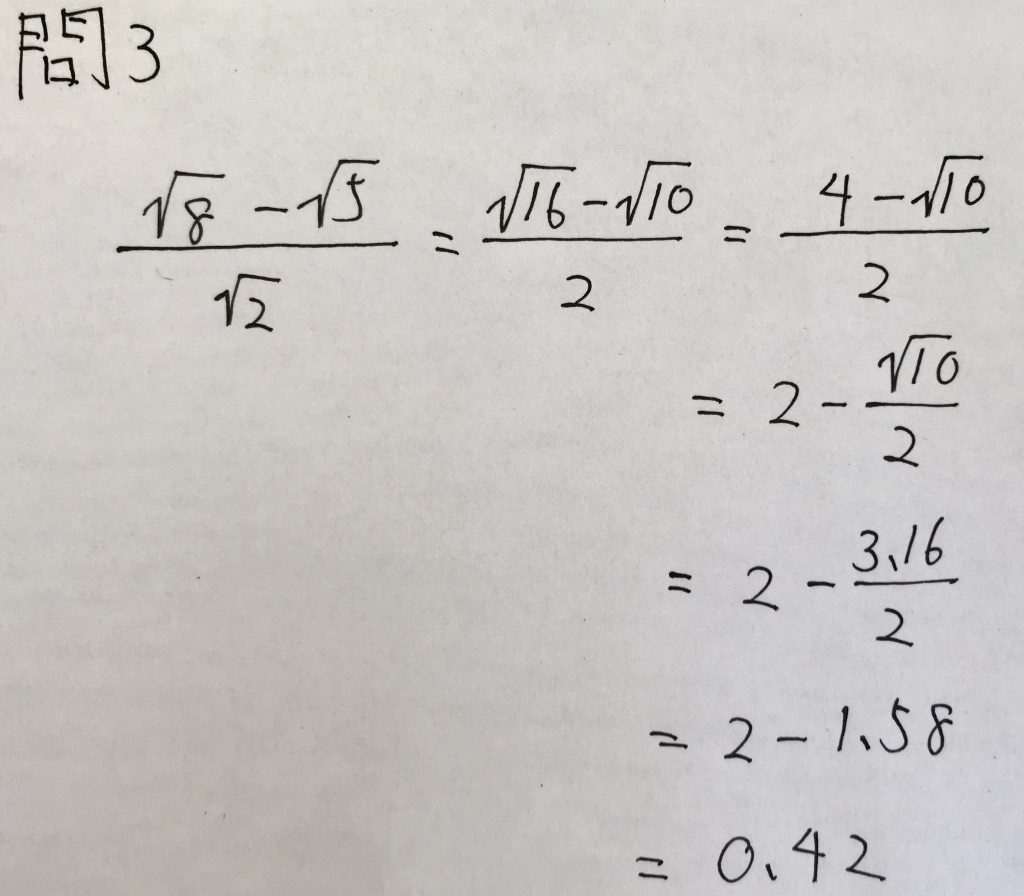
問4
「傾き＝yの増加量/xの増加量」の公式に当てはめれば終わりです。
以下、解答です。
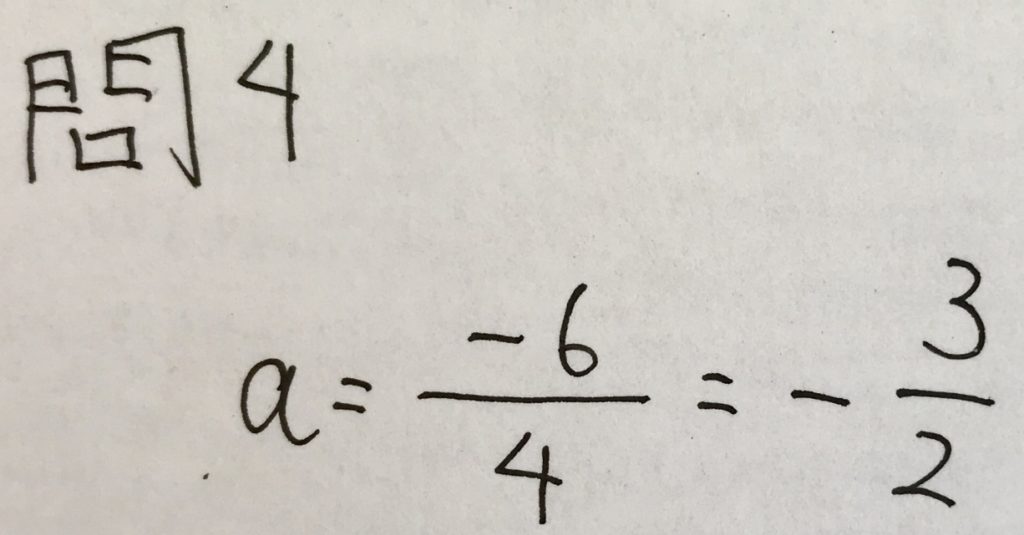
問5
図形問題というだけでアレルギーを発症して、捨てた子も多かったのではないでしょうか。
北海道公立高校入試の図形問題は易しいので、捨てちゃダメです。
学校のワークなどを使って、典型問題を理解した上で暗記して知識量を増やしていけば、図形問題は必ず解けるようになります。
以下、解答です。
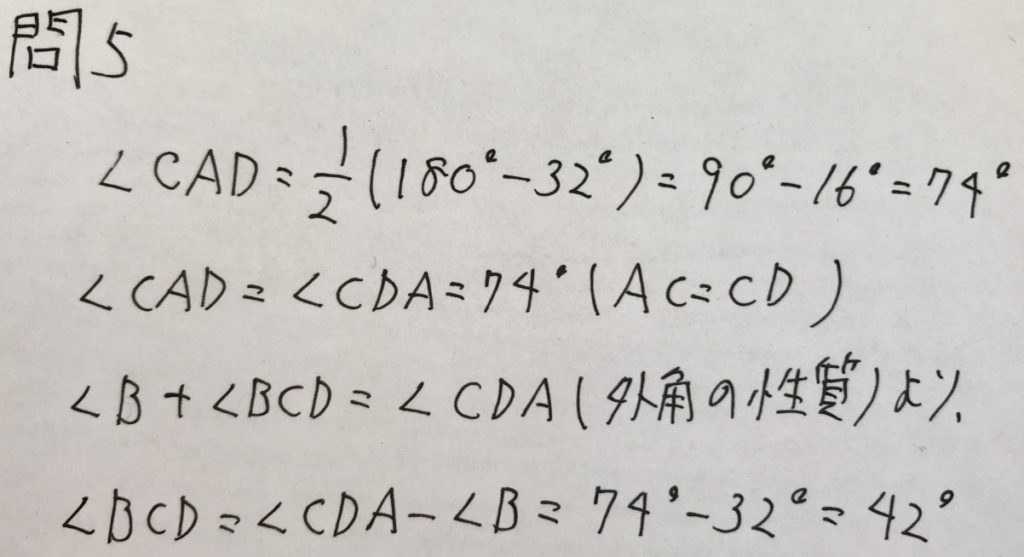
大問2 方程式・求値式
問1
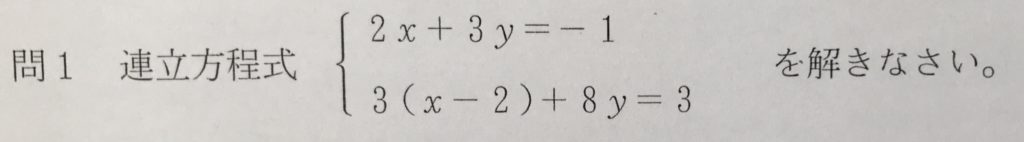
下の二元一次方程式を整理してから解きます。
以下、解答です。
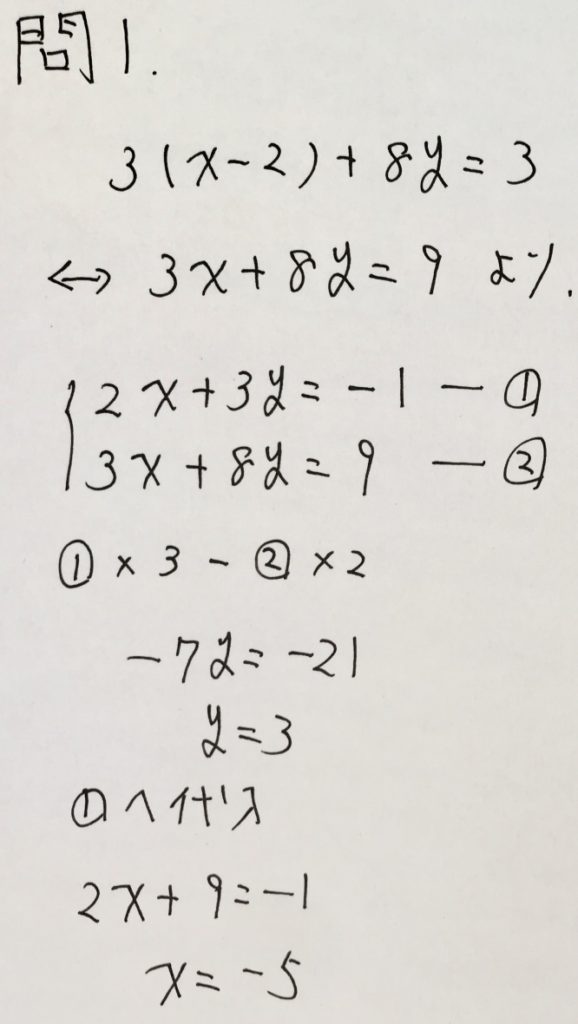
問2
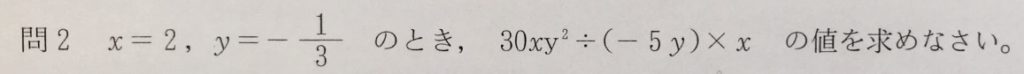
求値式を整理してから、xとyの値を代入します。
以下、解答です。
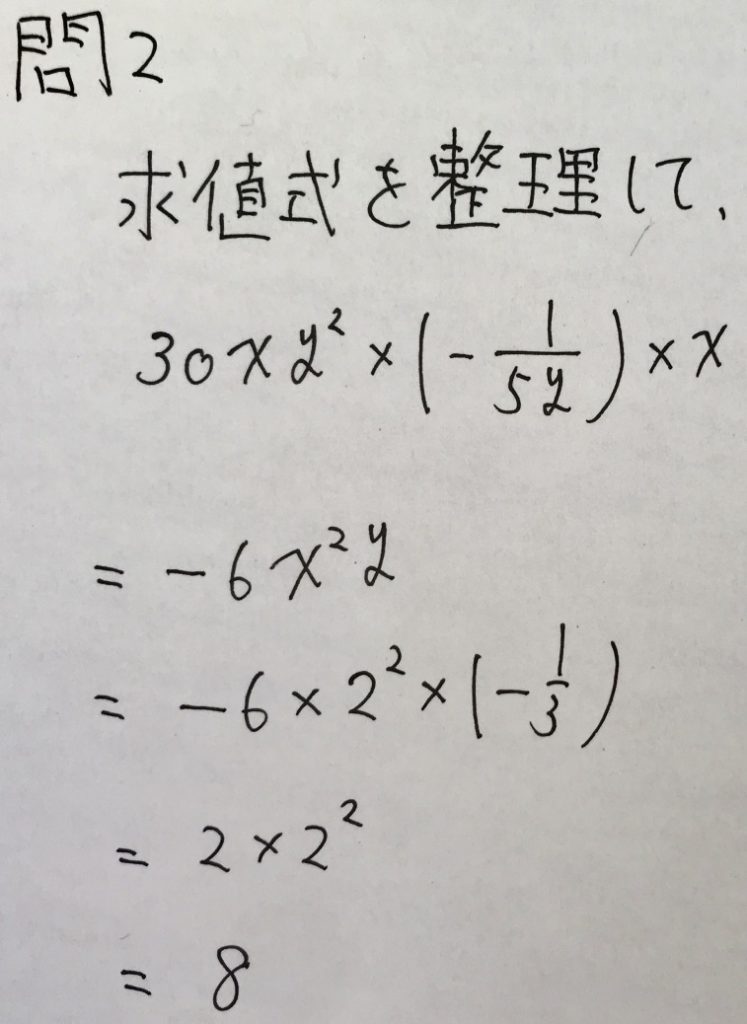
問3
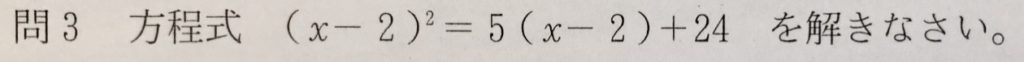
左辺から、二次方程式であることはすぐに分かるかと思います。
式を展開してもよいのですが、せっかく共通因数（x-2）があるので、
因数分解してから式の展開をして二次方程式を立式して、解を導く感じでやるとスマートでしょう。
以下、解答です。
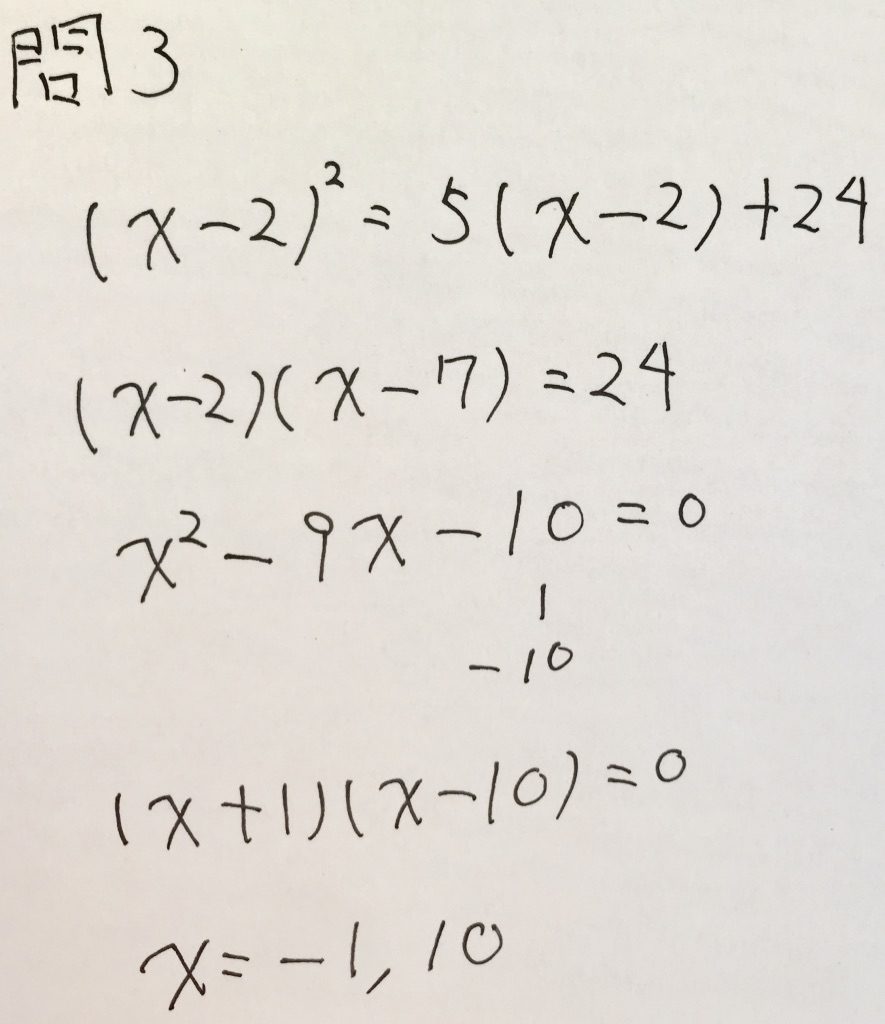
大問3 資料の解釈
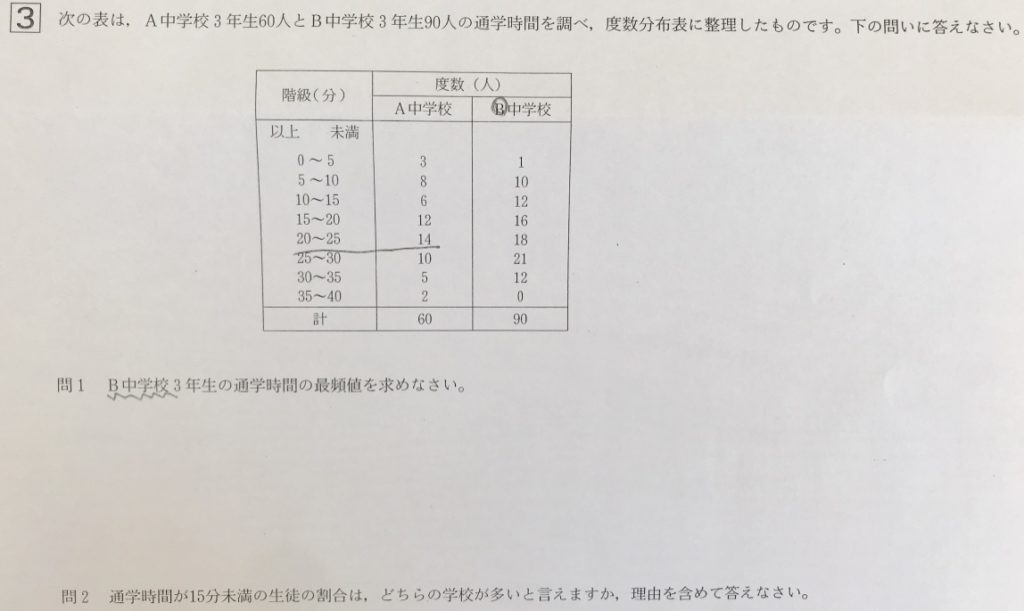
問1
最頻値とは、最も大きい度数の階級の階級値です。
代表値（平均値・最頻値・中央値）の違いを、しっかり抑えてください。
平成30年（2018年）の北海道公立高校入試が、良い演習になるでしょう。
以下、解答です。
問2
資料の解釈で「割合」と聞かれたら、相対度数です。
相対度数は分数で、分数とは割合で比でもある。
こういう根本的なことを知らないと、この問題は解けないでしょう。
以下、解答です。
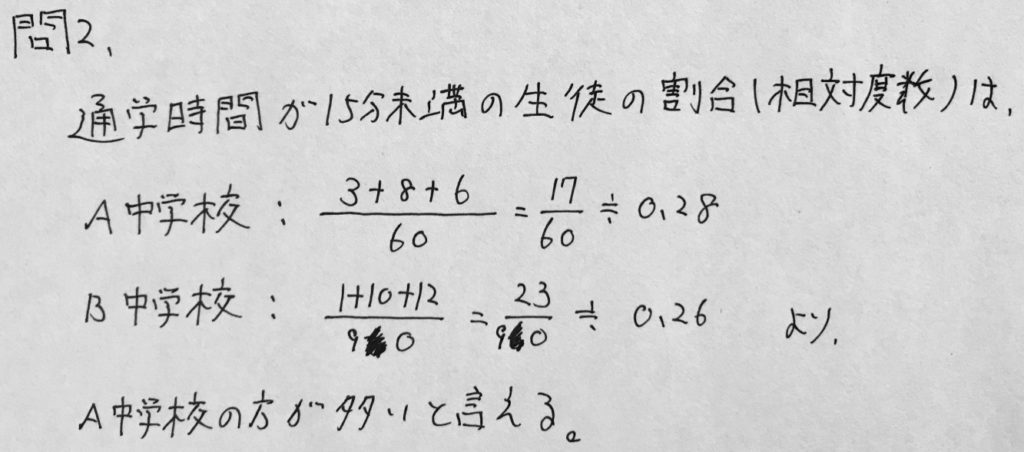
大問4 方程式・不定方程式
問1
ボーナス問題です。
以下、解答です。
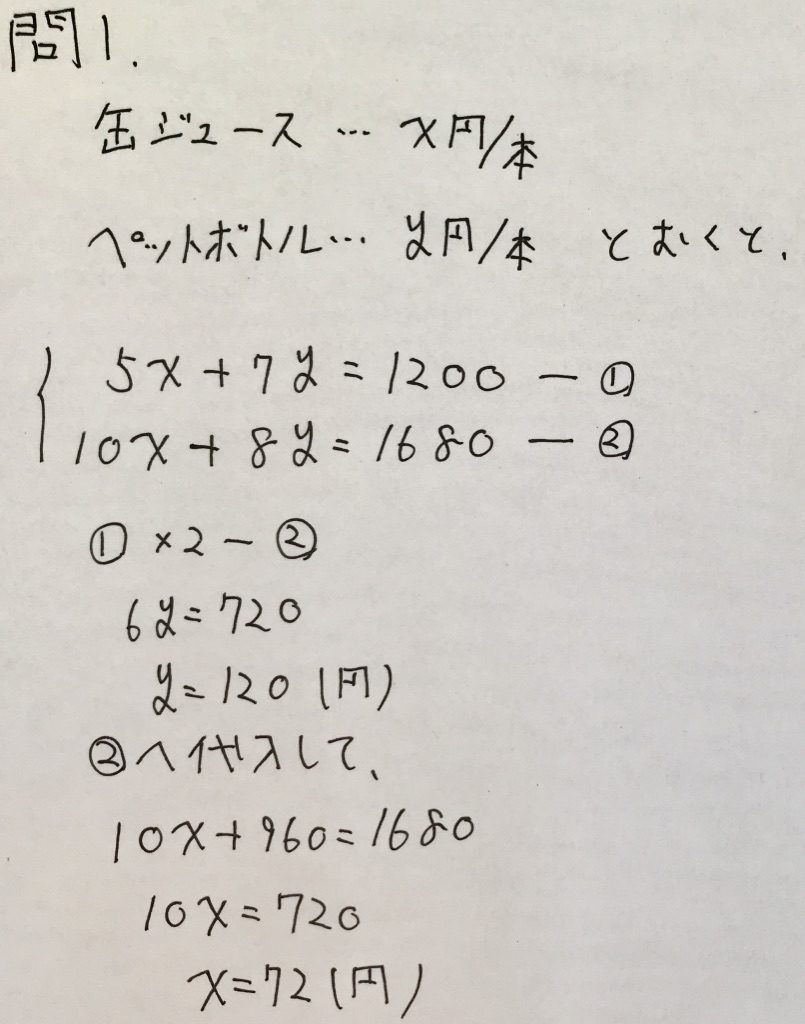
問2
四角形EFGHの面積は、長方形ABCDの面積から4つの三角形の面積を引けばよいことはすぐに分かるかと思います。
ここで、長方形ABCDかつ仮定より、△AEH≡△GCH、△BFE≡△DHGとなるので、
4つの三角形は、二つの長方形となることに気付くと、計算が簡単になります。
以下、解答です。
問3
今回の総合Aの中で、最も難しい問題です。
といっても、学校裁量問題の易しめのレベルなので、本番では確実に得点したい問題ではあります。
以下、解答です。
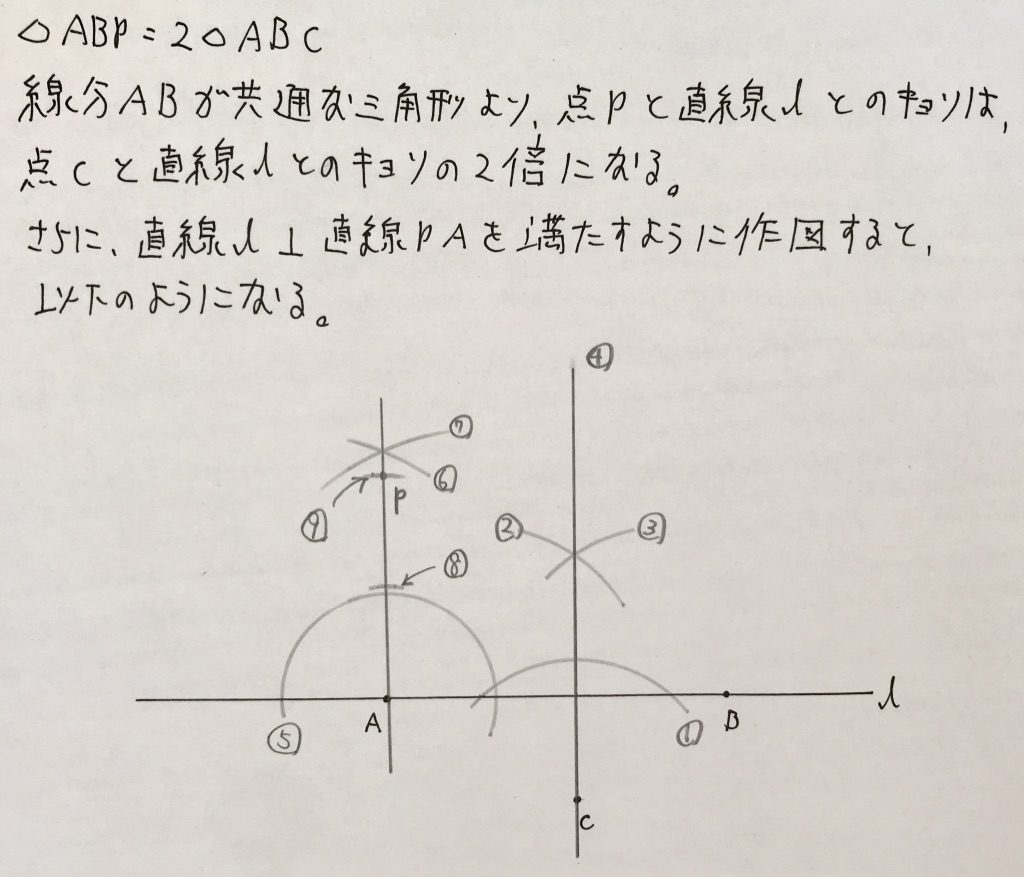
大問5 作図
直線上の1点から引いた垂線の作図を2回使います。
△ABP＝2△ABC、底辺ABが共通なので、直線lと点Pとの距離は直線lと点Cとの距離の2倍です。
類題として、平成30年度（2018年）の北海道公立高校入試の作図の問題があります。
以下、解答です。
大問6 一次関数
問1
△AOC＝6より、点Cの座標がすぐに求まります。
あとは、点A（y切片）と点Cの座標より、傾きを求めて終わりです。
以下、解答です。
問2
今回の総合A数学の中で、かなり難しい部類に入ります。
おそらく正答率は10％を切るのではないでしょうか。
関数で面積が等しいときたら、等積変形を使います。
しかし、△ACOと△BPCは共通な辺がありません。
が、a＝-1/4より△ACOの面積が求まります。
点Cはx軸上にあるので、△BPCを等積変形して、△ACOの面積で等式を立てればいけそうです。
以下、解答です。
大問7 図形の証明
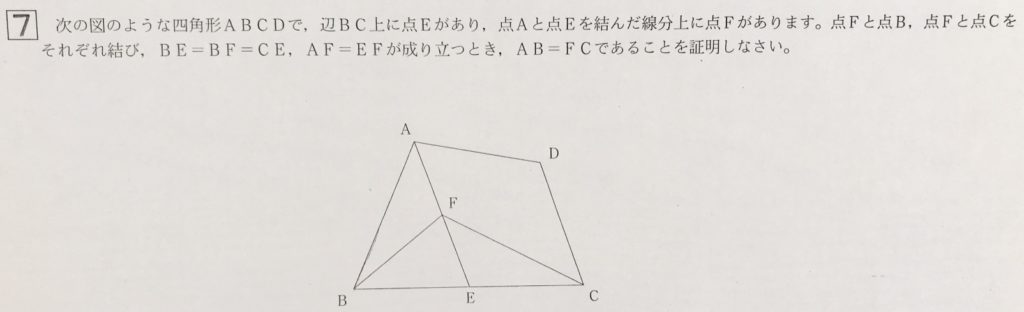
ボーナス問題です。
総合ABCの数学の図形の証明問題では、極端に易しい問題が出題されることがよくあります。
北海道公立高校入試の図形の証明問題は易しいので、典型問題の理解した上での暗記をして積み上げていけば、必ず解けるようになりますよ。
以下、解答です。
