指導経験20年以上のプロ家庭教師。北海道の高校受験に特化。勉強がとても苦手な子の指導が得意です。1回70分授業で、毎月の授業料は16,000円(月4回)〜30,000円(月12回)のみ、不透明な追加料金は一切ありません。
＞＞ブログ記事一覧（目次）
＞＞5教科・偏差値別オススメ問題集一覧
＞＞的中率60%以上！今年度の北海道公立高校入試「理科」はここが狙われる！家庭教師のそらの予想出題分野
■北海道公立高校入試のボーダー(合格)ライン・最低点の推移
＞＞北海道公立高校入試の道コン最低点推移のランク別まとめ
■北海道の公立高校の最終倍率推移
＞＞北海道の公立高校の最終倍率推移
■北海道公立高校入試の平均点推移と予想
＞＞北海道公立高校入試の平均点推移・各科目の正答率・人数分布・平均点予想まとめ
■北海道公立高校一般入試の合否判定の手順
＞＞【最新版】北海道公立高校一般入試の合否判定の手順の詳細まとめ
北海道公立高校入試過去問はこちら
★過去問
★模擬テストとリスニング対策
※模擬テストは1教科のみ表示。Amazonなどでは5教科すべて販売されています。
大問1 小問集合
問1
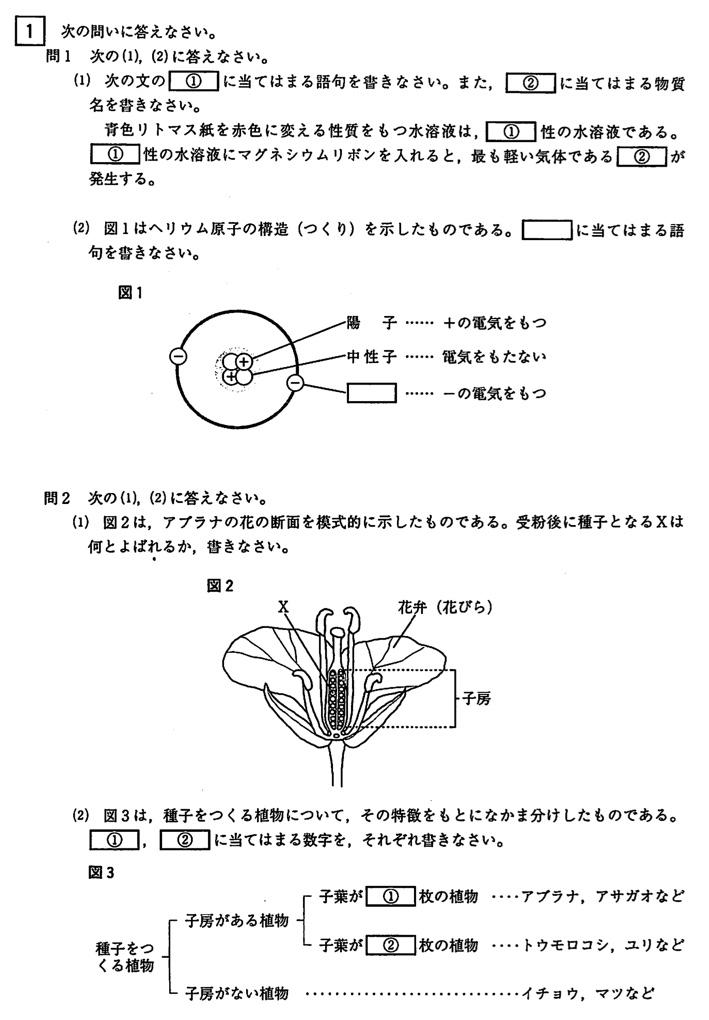
（1）
（答）①酸、②水素
酸性の特徴について問う問題です。
『塾技 理科80』を読んでいれば、瞬殺できますね。
酸性とは、水素イオン（H+）と水酸化物イオン（OH–）において、水中にH+のみ存在する「状態」です。
酸性の特徴としてこの他に、・BTB溶液が黄色になる、・電流が流れる、があります。
酸とは、水に溶かすとH+を放出する「物質」です。
酸は「物質」、酸性は「状態」と意味が異なりますので、要注意です。
酸と酸性、アルカリとアルカリ性の違いとそれぞれの特徴について、詳しく勉強してください。
（2）
（答）電子
原子の構造について問う問題です。
原子核には陽子と中性子があり、その周りを電子が回っています。
陽子は+の電気、電子は-の電気で、原子は陽子と電子を同数ずつもっており、それらが互いに電気を打ち消し合うため電気を帯びていません。
問2
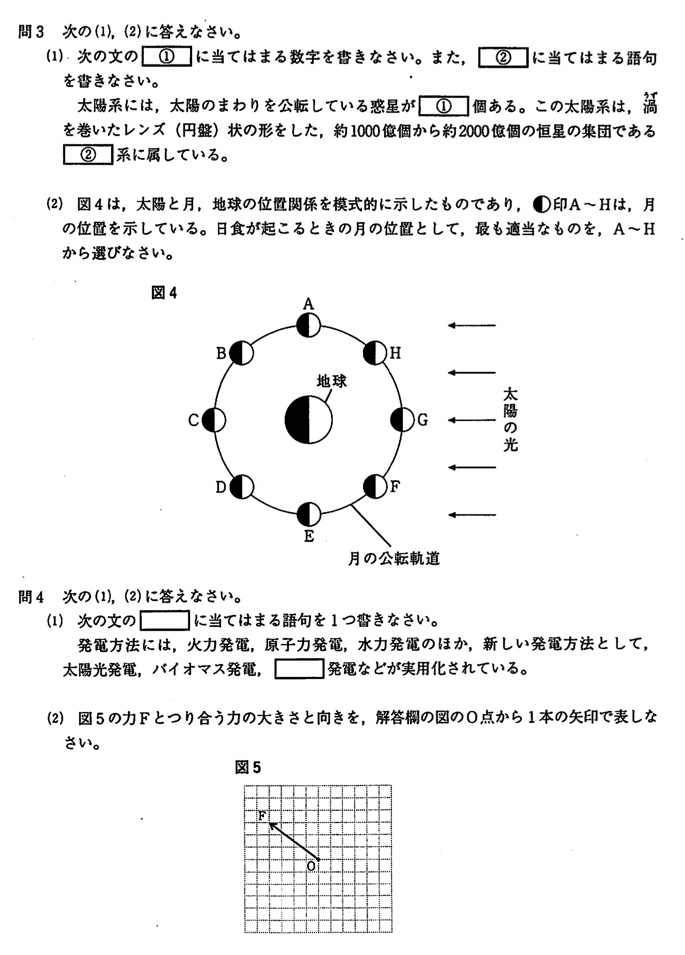
（1）
（答）胚珠
アブラナは被子植物—双子葉類—離弁花類です。
被子植物は胚珠が子房に包まれており、受粉して受精すると、胚珠は種子に、子房は果実になります。
基本中の基本ですね。
（2）
（答）①2、②1
双子葉類と単子葉類の子葉の枚数について問われています。
双子葉類は子葉が2枚、単子葉類は子葉が1枚ですね。
双子葉類と単子葉類において、葉のつくり、根のつくり、茎の道管・師管の場所の違いを押さえてください。
双子葉類の場合、以下のとおりです。
・葉の葉脈は網状脈
・根は主根と側根
・茎は維管束が輪状に並んでおり、形成層を挟んで内側が道管（水・肥料分が根毛→葉へ）外側が師管（葉の葉緑体にて光合成で作られたデンプンが夜間に葉→からだの各部へ）
・赤色に着色した水を吸わせると、茎の内側が赤く染まり、茎の断面に2本の赤い線が見られる
問3
（1）
（答）①8、②銀河
①
惑星は、水星-金星-地球-火星-木星-土星-天王星-海王星、の8つがあります。
内惑星と外惑星、地球型惑星と木星型惑星で分類できます。
それぞれの惑星の特徴について、詳しく勉強してください。
②
銀河系の内容については、問題文ごと暗記しましょう。
銀河系の内部（地球）から、銀河系の中心部の断面を見た姿が天の川であることも押さえてください。
（2）
（答）G
日食とは、月が太陽の光をさえぎって起こることから、答えは新月のGです。
日食での星の配置は、太陽-月-地球の順です。
月食とは、地球の影が月を覆い隠して起こることから、満月のCで起こります。
月食での星の配置は、太陽-地球-月の順です。
月は地球を西から東（反時計回り）に公転する衛星で、新月の位置から、右から満ちて右から欠けると覚えると、月の満ち欠けの様子が容易に分かるようになります。
問4
（1）
（答）風力
再生可能エネルギーについて問われています。
再生可能エネルギーとして、風力発電、波力発電、地熱発電、太陽光発電、バイオマス発電の5つを覚えましょう。
バイオマス発電はさらに突っ込んで、カーボンニュートラルの知識も押さえてください。
（2）
2力の釣り合いで、一直線上にある反対向きの2力の作図の問題です。
力Fと矢印の長さが同じで、向きが逆の矢印を作図すればOKです。
矢印の長さが力の大きさ、矢印の向きが力の向きです。
大問2 身のまわりの現象（物理分野・中1）
問1
（答）①イ、②イ
①
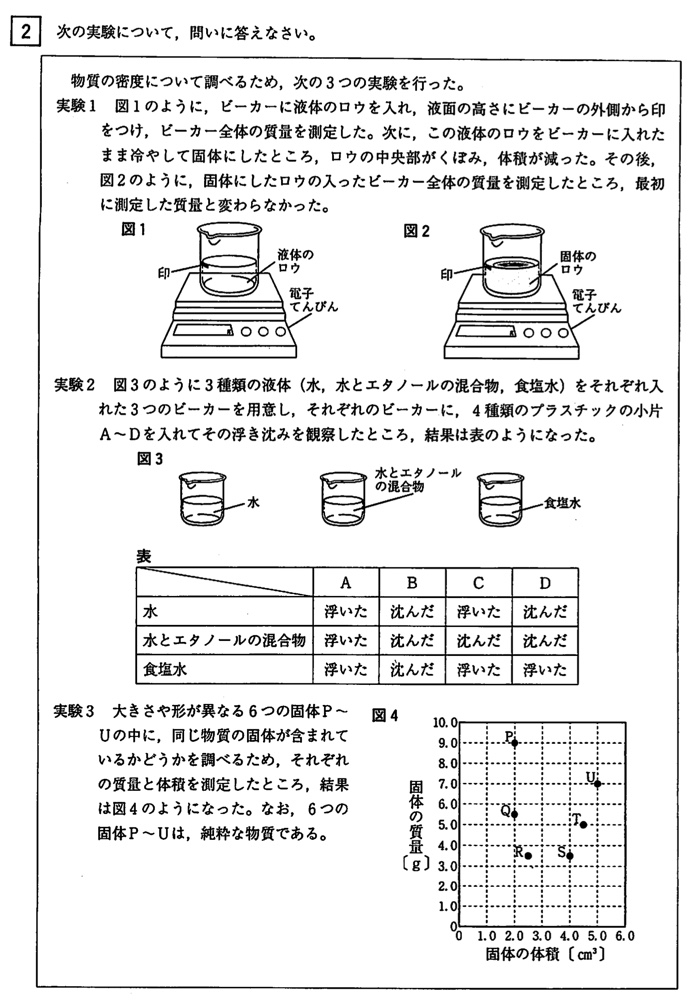
実験1より、ロウは液体→固体になると、質量は変わりませんが体積が減っていることが分かります。
密度の単位（g/cm3）より、液体→固体になると密度が増加します。
密度が大きい固体は、密度の小さい液体に沈みます。
②
水の場合、液体（水）→固体（氷）になると、例外的に体積が増加します。
密度の単位（g/cm3）より、液体（水）→固体（氷）になると密度が減少します。
密度が小さい固体（氷）は、密度の大きい液体（水）に浮きます。
水以外は液体→固体で密度が増加、水は液体（水）→固体（氷）で密度が減少は覚えましょう。
問2
（答）
密度の大きい順：B→D→C→A
説明：小片Cは水に浮いて、小片Dは水に沈んだから
まず、小片Aは全ての液体に浮いているので、密度は最小です。
小片Bは全ての液体に沈んでいるので、密度は最大です。
小片CとDの違いは、水に浮いたか沈んだかです。
小片Cは水に浮いていますが、小片Dは水に沈んでいるので、密度は小片C＜小片Dです。
なお、問題文でプラスチックの話が出てきているので、代表的なプラスチック5つ（PET・PE・PVC・PS・PP）の違いも押さえてください。
プラスチックの問題はずっと出題されていないので、そろそろ出てきてもおかしくありません。
問3（1）
（答）針金で押して水に沈め
教科書に載っているはなしです。
問題集だけでなく、必ず教科書の2〜3読もしてください。
問3（2）
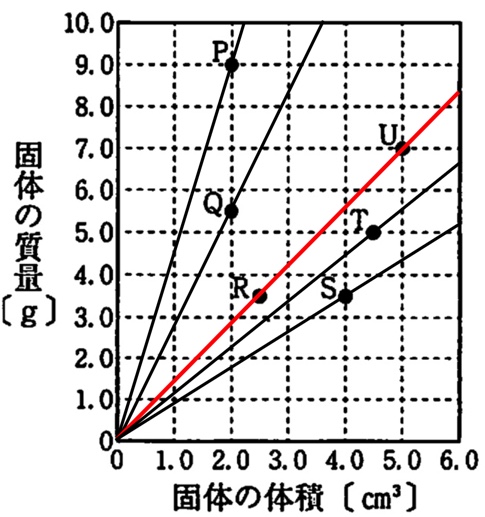
（答）①R、②U
図4のグラフの縦軸が質量（g）横軸が体積（cm3）なので、密度（g/cm3）のはなしをしています。
「同じ物質の固体」とは、密度が同じ物質の固体という意味です。
図4のグラフにおいて、グラフの傾きが密度（g/cm3）なので、同一直線上にあるRとUが答えになります。
問3（3）
（答）固体：P、体積：4cm3
密度が4.5g/cm3において、体積が2cm3のとき質量は9gとなるので、固体Pが答えです。
固体Pの質量が18gのときの体積（cm3）は、密度の単位（g/cm3）に注意して計算するだけです。
密度(g/cm3)=質量(g)/体積(cm3)
体積(cm3)=質量(g)/密度(g/cm3)=18g/(4.5g/cm3)=180/45cm3=4cm3
大問3 天気とその変化（地学分野・中2）
問1（1）
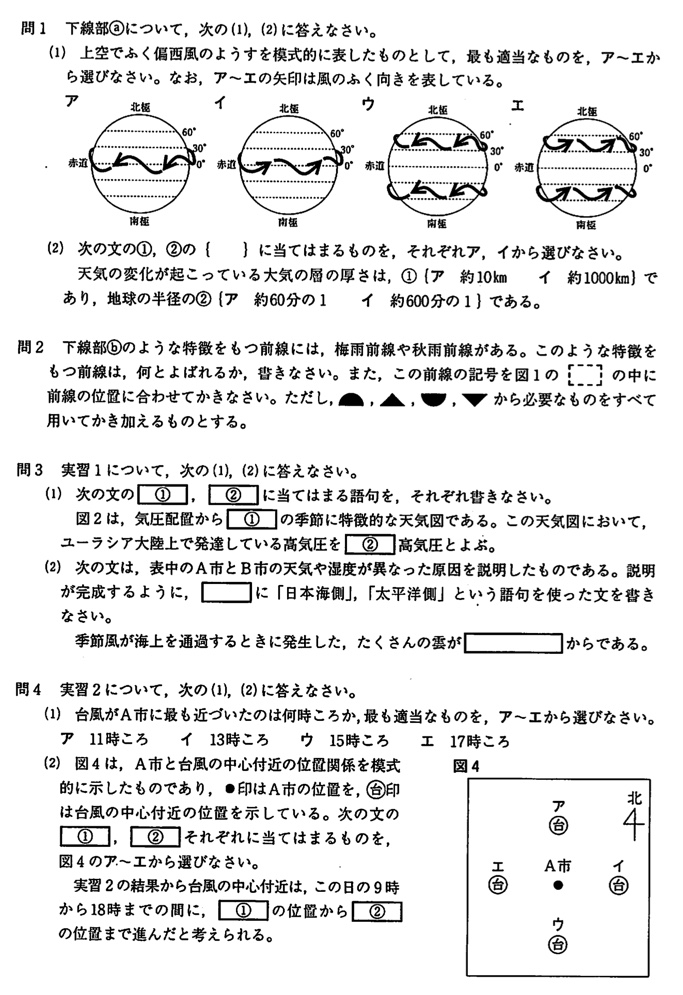
（答）エ
偏西風は漢字のとおり西風（西から東に吹く風）です。
偏西風は北緯30〜60度で吹いています。
偏西風は北半球だけでなく、南半球でも吹いていることに要注意です。
偏西風以外にも、極偏東風と貿易風についても押さえてください。
問1（2）
（答）①ア、②イ
天気の変化が起こっている大気は対流圏です。
対流圏は地上約10kmくらいまでで、対流がさかんに起こっています。
地球の半径は6400kmなので、対流圏は地球の半径の約600分の1になります。
対流のうち、水平方向の動きを風、上下方向の動きを気流といいます。
風として、陸風と海風と季節風があります。
気流として、上昇気流（低気圧）と下降気流（高気圧）があります。
それぞれの特徴について、詳しく勉強してください。
陸風と海風は過去8年間で入試に出題されていないので、そろそろ出るかもしれません。
問2
（答）
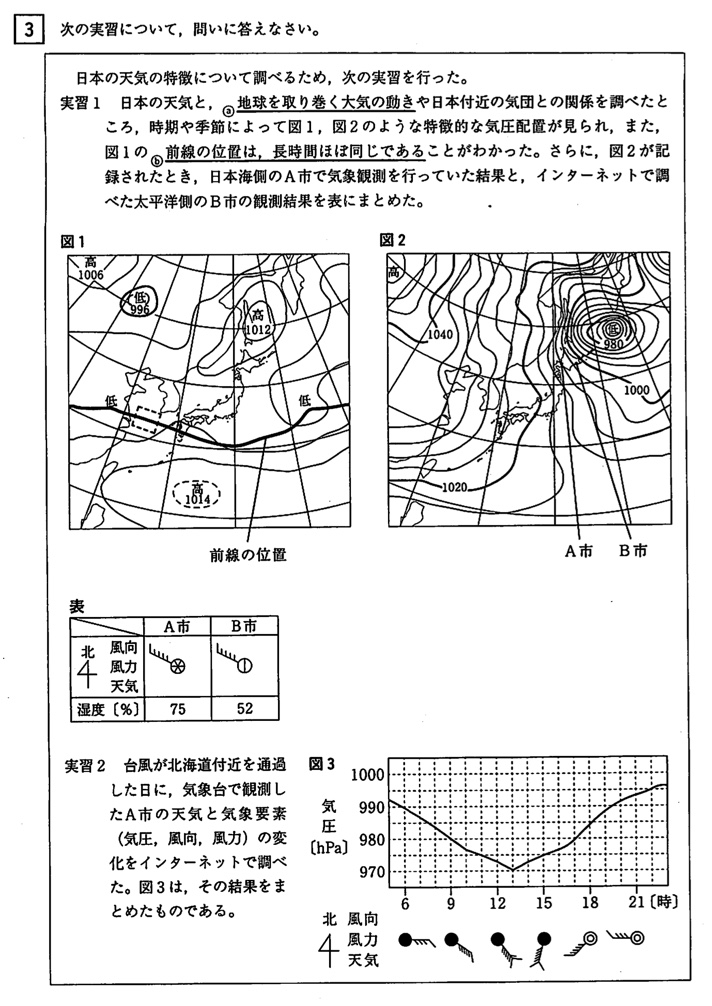
図1を見た瞬間に、梅雨の時期の天気図だと捉えられるのが理想です。
梅雨の時期には、オホーツク海気団と小笠原気団がほぼ釣り合い、両者の境に停滞前線である梅雨前線ができます。
停滞前線の記号は、解答例のとおりです。
問3（1）
（答）①冬、②シベリア
図1は、西高東低の気圧配置で、等圧線が縦縞となっていることから、冬の時期の天気図です。
図1を見た瞬間に、冬の時期の天気図だと捉えられるのが理想です。
問3（2）
（答）日本海側で雪を降らせ、水蒸気を失った乾いた空気が太平洋側に下降した。
冬はシベリア気団が発達して、冷たいユーラシア大陸（高気圧）から暖かい日本海（低気圧）に向かって、北西の季節風が吹きます。
シベリア気団は冷たく乾燥しているので、季節風は日本海上で水蒸気と熱を補給して、日本の山脈にぶつかって上昇気流が発生し、日本海側に雪を降らせます。
雪を降らせ水分を失った空気は、山脈を降りるときに乾燥した風となるため、太平洋側では乾燥した晴れの日が続きます。
大問4 生命の連続性（生物分野・中3）
問1
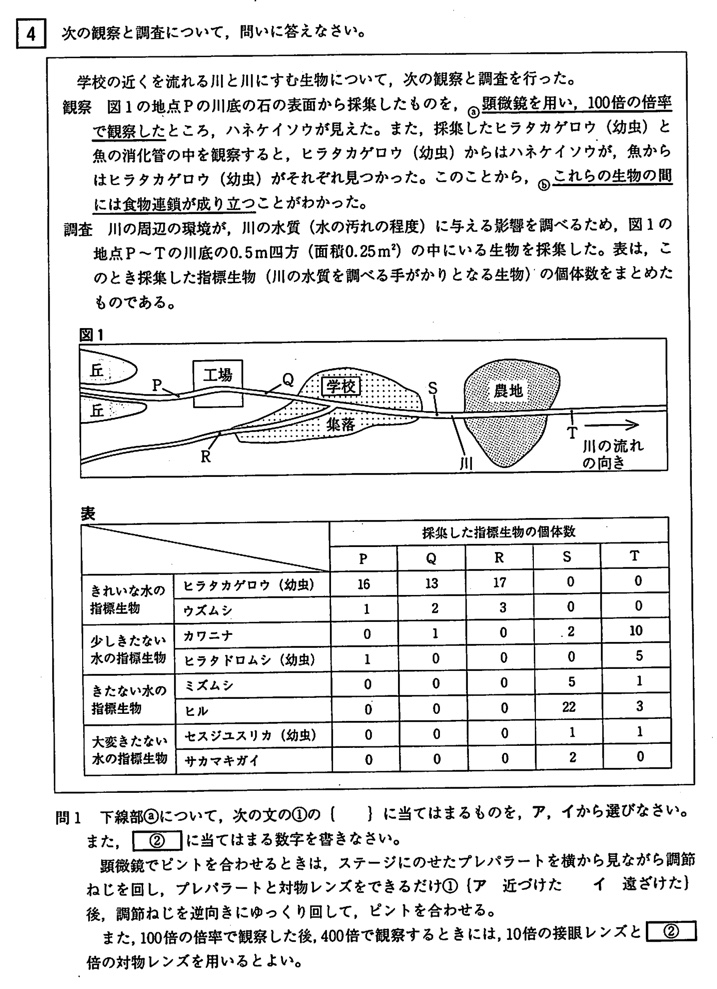
（答）①ア、②40
ステージ上下式・鏡筒上下式顕微鏡のはなしをしています。
ピントの合わせ方については、問題文ごと暗記しましょう。
10倍の接眼レンズで100倍の倍率で観察するときは、10倍の対物レンズを使います。
10倍の接眼レンズで400倍の倍率で観察するときは、40倍の対物レンズを使います。
対物レンズは、最初は低倍率のものから使用していきます。
接眼レンズは短いものほど、対物レンズは長いものほど倍率が高くなります。
顕微鏡の倍率が高くなると、視野が狭く明るさが暗くなることも押さえてください。
顕微鏡の倍率が2倍、3倍となると、視野と明るさは1/4倍、1/9倍になります。
問2（1）
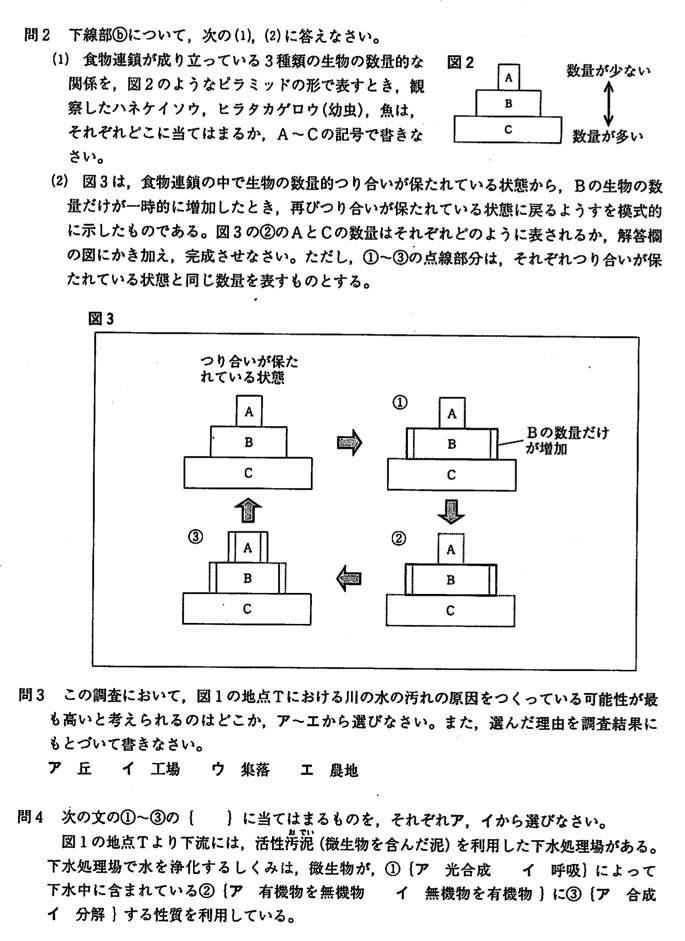
（答）ハネケイソウ：C、ヒラタカゲロウ：B、魚：A
観察の文章を注意深く読めば、答えが簡単に出せます。
「ヒラタカゲロウ（幼虫）からはハネケイソウが」「魚からはヒラタカゲロウ（幼虫）が」から、ピラミッドの頂点は魚、真ん中はヒラタカゲロウ（幼虫）、一番下はハネケイソウになります。
問2（2）
Bが増加すると、Bを食べるAは増加し、Bに食べられるCは減少します。
問3
（答）
記号：ウ
理由：きたない水の指標生物の個体数が、地点P、Q、Rが0であるのに対し、地点Sで最も多くなっているから。
まず、表に以下のように記入すると分かりやすくなります。
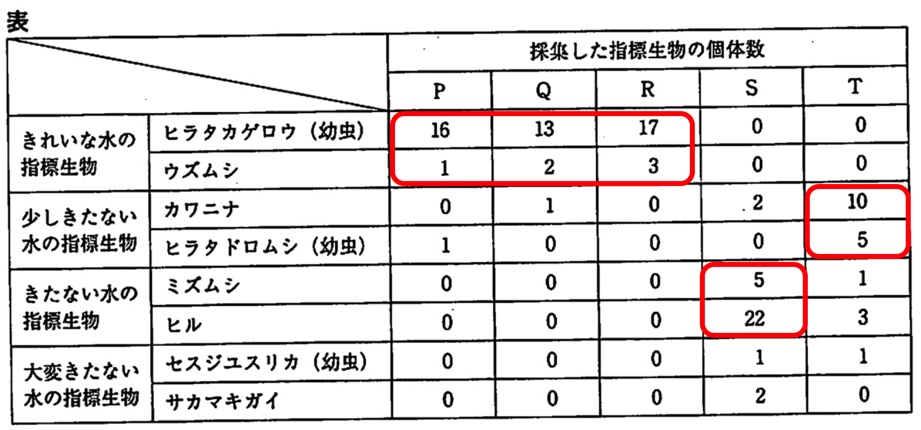
地点P、Q、Rでは、きれいな水の指標生物がほとんどで、きたない水の指標生物の個体数がゼロです。
しかし、集落を通過後の地点Sできたない水の指標生物がほとんどを占めていることから、地点Tでの川の汚れの原因をつくっているのは、集落であると推測できます。
なお、地点Tではきたない水の指標生物が減り、少しきたない水の指標生物がほとんどを占めていることから、農地で水が浄化されていることが分かります。
問3
（答）①イ、②ア、③イ
呼吸のメカニズムについて問われています。
生物は呼吸により、酸素を使って有機物を無機物に分解し、エネルギーを得ています。
対して光合成では、植物が光エネルギーを利用して、二酸化炭素と水から有機物と酸素を合成しています。
呼吸と光合成の違いをしっかり押さえてください。
大問5 電流とその利用（物理分野・中2）
問1（1）
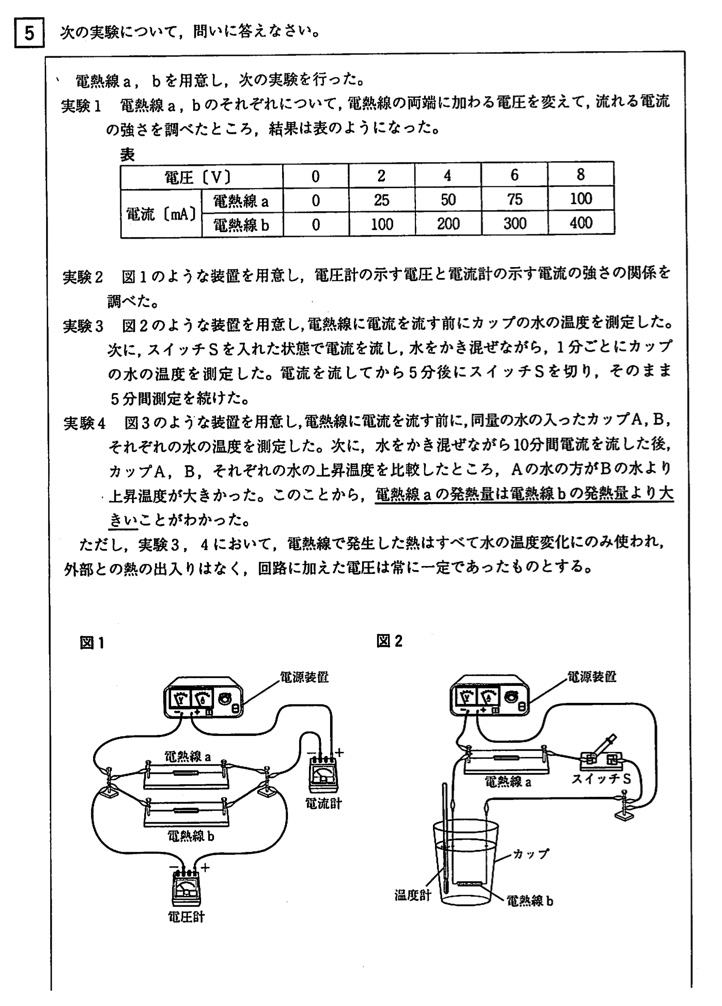
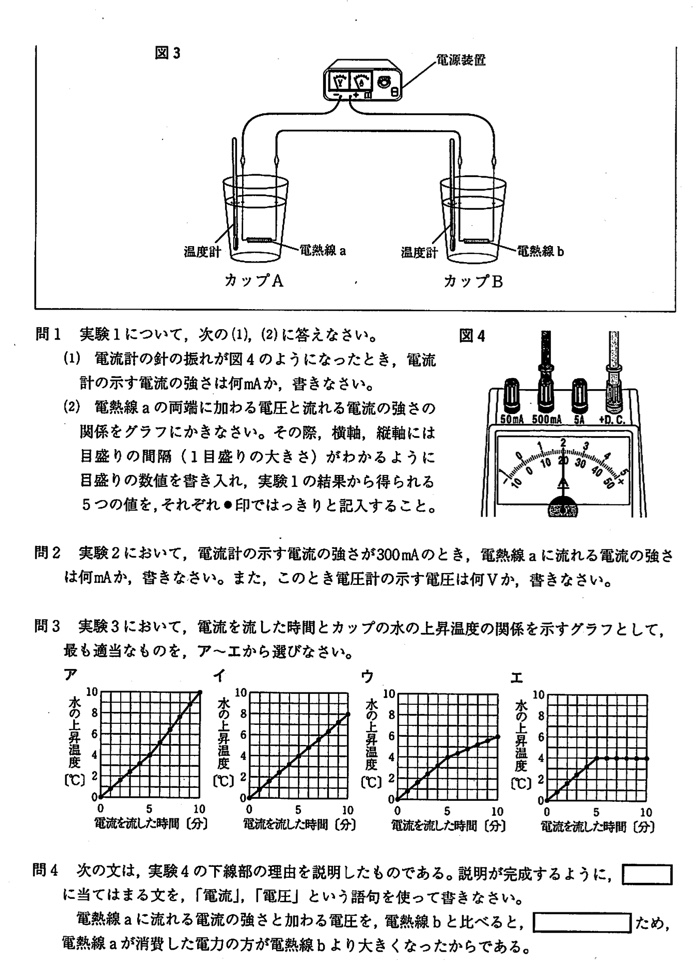
（答）200mA
電流計のマイナス端子が500mAなので、電流の強さは200mAです。
マイナス端子が50mAだったら、電流の強さは20mAです。
マイナス端子が5Aだったら、電流の強さは2Aです。
回路を流れる電流が不明のときは、5Aに接続します。
電圧計も同じようにして接続します。
電流計は直列に、電圧計は並列に接続することも合わせて覚えましょう。
問1（2）
表にある電熱線aの情報をグラフ化するだけです。
ここで、電熱線aとbの抵抗値を求めておきます。
V=I×R ⇔ R=V/I
電熱線a=4V/50mA=4/(50/1000)Ω=(4×1000)/50Ω=4×20Ω=80Ω
電熱線b=4V/200mA=4/(200/1000)Ω=(4×1000)/200Ω=4×5Ω=20Ω
問2
（答）
電流の強さ：60mA
電圧：4.8V
・電流の強さ
並列回路なので、電流の比＝抵抗の比の逆比となります。
電熱線aの抵抗：電熱線bの抵抗＝80:20＝4:1より、
電熱線aの電流：電熱線bの電流＝1:4（全体で5）
となります。
回路全体の電流が300mAより、電熱線aの電流は、
電熱線aの電流=300mA×frac1/5=60mA
（別解）
電熱線aの電流をIとすると、電熱線bの電流は300-Iと表せます。
並列回路なので、電熱線aの電圧と電熱線bの電圧は等しいことから、オームの法則より、電熱線aの電流をIを以下のように計算できます。
V=I×R
I×80=(300-I)×20⇔4I=300-I⇔5I=300⇔I=60mA
・電圧の値
オームの法則より、以下のように計算できます。
V=I×R=60mA×80Ω=4800mV=4.8V
問3
（答）イ
図2は並列回路なので、スイッチを切っても電熱線bにかかる電圧は変わらず、電流の強さも変わりません。
水の上昇温度は発熱量（電気エネルギー）Q(J)に比例します。
発熱量Q(J)は、消費電力P(W)=P(J/s)と時間との積で表されます。
P(W)=P(J/s)=I(A)×V(V)
Q(J)=P(J/s)×t(s)=I(A)×V(V)×t(s)
I(A)×V(V)の値が一定なので、Q(J)は時間にのみ比例するグラフとなります。
以上から、答えはイです。
（別解）
水の上昇温度と発熱量は、以下の関係となっています。
Q(J)=4.2×水の質量(g)×水の上昇温度(℃)
I(A)×V(V)×t(s)=4.2×水の質量(g)×水の上昇温度(℃)
水の上昇温度(℃)=(I(A)×V(V))/(4.2×水の質量(g))×t(s)
電流・電圧・水の質量は一定なので、「水の上昇温度=定数×時間」となるので、原点を通る直線となり、答えはイとわかります。
問4
（答）電流の大きさは等しいが、電圧は電熱線aの方が大きい
発熱量は、以下の式で表されます。
Q(J)=P(J/s)×t(s)=I(A)×V(V)×t(s)
t(s)=10×60s=600s、で一定です。
図3は直列回路より、電熱線aと電熱線bの電流の強さは同じです。
直列回路において、電圧の比＝抵抗の比となるので、
電熱線aの電圧:電熱線bの電圧=80Ω:20Ω=4:1
より、電熱線aの電圧の方が大きくなるので、発熱量は電熱線aの方が大きくなります。