【2018年】北海道公立高校入試「理科」の過去問を詳しく解説（難しい！）使える画像付き！！

 

＞＞的中率60%以上！今年度の北海道公立高校入試「理科」はここが狙われる！家庭教師のそらの予想出題分野

 

北海道公立高校入試過去問はこちら

★過去問

★模擬テストとリスニング対策

※模擬テストは1教科のみ表示。Amazonなどでは5教科すべて販売されています。

大問1　小問集合

 

 

問1

（1）

（答）被子

種子植物で、胚珠が子房に包まれている植物は、被子植物です。

アブラナとエンドウは被子植物の中の、双子葉類です。

アブラナは花弁4枚の離弁花で、おしべは6本のうち4本が長く、2本は短いです。

エンドウは、花弁がおしべとめしべを包み込み、おしべはめしべを包み込んでおり、自家受粉が行われます。

おしべは10本のうち9本がもとがくっつきめしべを包み込み、1本だけ離れています。

種子植物で、胚珠が子房に包まれていない植物は、裸子植物です。

 

（2）

（答）マグマ

火山の地下にあり深成岩となるのは、マグマです。

マグマが地表に出てきたのが、溶岩です。

マグマが冷えてできる岩石には火成岩がありますが、マグマの冷え方と場所により、火山岩と深成岩に分けられます。

また、マグマの二酸化ケイ素の含有量・温度により、溶岩の吹き出し方や火山のかたちが変わってきます。

マグマに含まれる造岩鉱物の含有量により、火山岩と深成岩の種類が変わってきます。

 

（3）

（答）ひげ根

双子葉類と単子葉類の根の違いについて、問題文ごと暗記しましょう。

単子葉類の種類ですが、イネ・トウモロコシ・スズメノカタビラ・ユリ・チューリップ・アヤメ・ツユクサ・タマネギの9種類を覚えましょう。

 

（4）

（答）震央

震源と震央の違いについて、問題文ごと暗記しましょう。

地震の計算問題では、震源の深さがごく浅い地震とみなし、震源距離＝震央距離として計算しています。

初期微動継続時間は震源距離に比例する、という知識も押さえてください。

 

（5）

（答）力学的エネルギー

位置エネルギー ＋ 運動エネルギー＝力学的エネルギー＝一定、です。

エネルギーは移り変わる性質があるので、物体の運動状態により位置エネルギーと運動エネルギーは移り変わりますが、その和である力学的エネルギーの値は常に一定です。

なめらかな斜面を下る小球、ふりこの運動について、位置エネルギーと運動エネルギーの状態を把握できるようになってください。

 

（6）

（答）主要動

地震が発生すると、速度の異なるP波とSが同時に発生します。

速度の大きいP波が最初に到達して初期微動が、速度の小さいS波が次に到達して主要動が発生します。

P波が到達してからS波が到達するまでの時間を、初期微動継続時間（p-s時間）といい、初期微動継続時間は震源距離に比例します。

 

（7）

（答）融点

沸点と融点の違いは、問題文のとおりです。

しかし、これだけでは何にもなりませんので、状態変化のグラフを通じて、沸点と融点を覚えましょう。

融点と沸点では時間とともに温度が変わりません。

これは、融点の場合、加えた熱がすべて固体を溶かすのに使われ、沸点の場合、加えた熱がすべて液体を気体にするのに使われるからです。

 

（8）

（答）受精

有性生殖では、体細胞が減数分裂して染色体が半分になって、生殖細胞が作られます。

生殖細胞は、被子植物の場合は精細胞と卵細胞、動物の場合は精子と卵と呼びます。

精子（精細胞）と卵（卵細胞）が受精して受精卵ができ、体細胞分裂を繰り返して個体へと変化していきます。

受精卵が体細胞分裂を繰り返して、自分で食物をとることができる個体となる前のものを胚といいます。

そして、受精卵が体細胞分裂を繰り返して個体へと変化していくことを発生といいます。

 

問2

（答）対流

問題文ごと暗記しましょう。

 

問3

（答）ア、オ

砂糖、プラスチック、ロウは、燃やす（酸化）と二酸化炭素と水が発生するので有機物です。

食塩は燃やしてもパチパチはねるだけ、鉄は燃やす（酸化）すると酸素と化合して酸化鉄になるだけです。

有機物で非電解質であるのは、砂糖とエタノールです。

プラスチックでは、PET・PE・PVC・PS・PPの5種類について、熱したときのようす、密度（水に浮くか否か）を押さえてください。

 

問4

（答）ア、エ

生産者は植物ですので、選択肢アのアサガオと、選択肢エのゼニゴケになります。

選択肢ウのメダカは植物を食べるので、消費者です。

選択肢イとオとカは菌類や細菌類、土の中の小動物なので、分解者です。

生産者・消費者・分解者において、有機物、二酸化炭素と酸素、窒素のながれについて押さえてください。

 

問5

（答）

 

星の日周運動についての問題です。

星は北の空では、北極星を中心に反時計回りに1時間に15°ずつ動いて見えます。

4時間後の恒星Aの位置は、もとの位置から60°動いて見えます。

問題文の図は円周が12等分されているので、北極星ととなりあう恒星とのなす角度は30°（360°÷12）なので、恒星Aの位置は、もとの位置から二つ分反時計回りにずれます。

 

問6

（答）9g

質量パーセント濃度の式に、溶質（硝酸カリウム）と溶媒（水）の質量を代入して計算すれば終わりです。

質量パーセント濃度（％）=硝酸カリウム/(硝酸カリウム+水)×100=10

1/(1+x)×100=10⇔1/(1+x)×10=1⇔10=1+x⇔x=9

 

問7

（答）40W

仕事と仕事率の式は、以下のとおりです。

仕事(J)=加えた力(N)×移動距離(m)

仕事率(W)=仕事率(J/s)=仕事(J)/仕事をするのに要した時間(s)

この問題では、「一定の速さで（物体を）持ち上げる」と書かれているので等速直線運動をしており、重力と持ち上げる力が釣り合っています。

以上から、仕事率は以下のように計算できます。

仕事(J)=100N×0.8m=80J

仕事率(W)=仕事率(J/s)=80J/2s=40J/s=40W

大問2　天気とその変化（地学分野・中2）

 

問1

（答）①：11、②：12、③イ

①と②

表1のタオルの質量の変化を引き算して求め、比較すれば終わりです。

10時→11時は14g、11時→12時は16g、12時→13時は14g、13時→14時は12gなので、タオルの質量の減少量が最も大きかった時間帯は、11時から12時までの1時間です。

③

湿度が低いと水の蒸発量が増えるので、風を当ててタオルの表面付近の湿度を下げるとよいです。

乾湿計において、乾球と湿球の示度（温度）差が大きいと、湿度が低くなります。

これは、湿度が低いと空気中に含まれる水蒸気量が少なく、湿球に巻いた濡れたガーゼの水がたくさん蒸発して気化熱により、湿球の温度が大きく下がるからです。

反対に、湿度が高いと、湿球に巻いた濡れたガーゼの水があまり蒸発しないので、乾球と湿球の示度（温度）差が小さくなります。

 

問2

（答）①：5.8、②11

①

湿度の公式を変形して水蒸気量を求めます。

湿度（％）=水蒸気量(g/m³)/飽和水蒸気量(g/m³)×100⇔水蒸気量(g/m³)=湿度（％）×飽和水蒸気量(g/m³)/100

水蒸気量(g/m³)=(40×14.5g/m³)/100}=0.4×14.5g/m³=5.8g/m³

表2より、4℃のときの飽和水蒸気量が6.4g/m³と5.8g/m³より高いので、12時のとき水滴は付きません。

②

表2より、3℃のときの飽和水蒸気量が5.9g/m³となるので、それよりも水蒸気量が多くなる時間帯を計算して探します。

飽和水蒸気量のグラフをイメージして、気温が高く湿度が高いほど水蒸気量は多くなることが分かります。

表1より、10時〜13時において湿度は似たり寄ったりの値ですので、気温が高い11時に目をつけて、水蒸気量を計算します。

11時における水蒸気量は、

水蒸気量(g/m³)=(39×15.4g/m³)/100≒0.4×15.4g/m³=7.6g/m³

より、3℃のときの飽和水蒸気量5.9g/m³よりも水蒸気量が多いので、3℃のとき水滴がつきます。

 

問3（1）

（答）

最初：Z、ウ

最後：Y、ア

図2より、A市に温暖前線が近づいていることが分かります。

温暖前線は、暖気が寒気の上にはいあがり、緩やかな上昇気流が生じるため、乱層雲、巻層雲、巻雲と、層状の雲が生じます。

温暖前線が近づくと、巻雲、巻層雲、乱層雲の順で雲が通過していきます。

巻雲、巻層雲が通過中はくもり空、乱層雲が通過中は弱い雨が降ります。

以上から、最初に通過するのは巻雲、最後に通過するのは乱層雲です。

雲の写真ですが、形からしてZが巻雲、Yは空が暗いので乱層雲であると言えます。

 

問3（2）

（答）①2、②イ、③ク

①

雲ができるメカニズムについて問われています。

図4において、上空2kmのとき湿度が100%と露点に達しているので、雲が発生し始めています。

②

温暖前線の図をイメージして、温暖前線が近づくと巻雲、巻層雲、乱層雲が通過しますが、これらの雲は高い位置に順に発生しています。

よって、温暖前線が接近すると、雲の高さは低くなります。

③

雲の高さが低くなるということは、それだけ低い位置で露点に達し、湿度が100％になるということです。

選択肢カとキは図4より高い位置で湿度が100％になっているので不適で、消去法により選択肢クとなります。

大問3　化学変化とイオン（化学分野・中3）

 

 

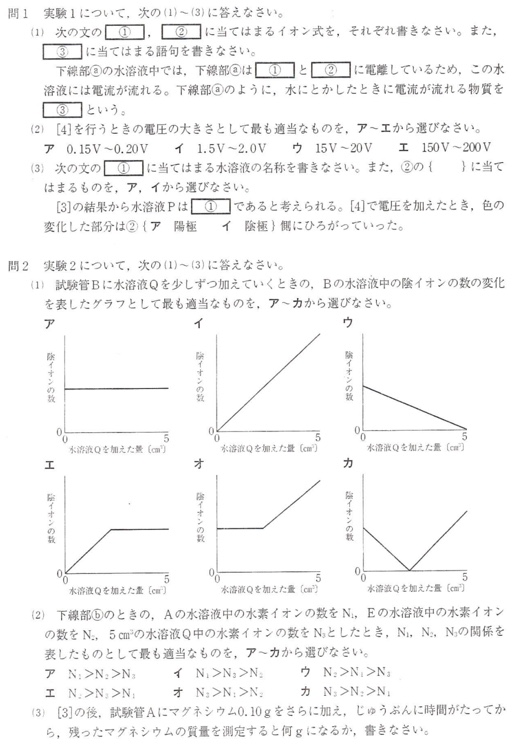
問1（1）

（答）①：Na⁺、②：Cl^–、③電解質

単なる知識問題です。

紙を塩化ナトリウム（食塩水）でしめらせるのは、電流が流れるようにするためです。

塩化ナトリウム（食塩水）の他にも、硫酸ナトリウム水溶液や硫酸カリウム水溶液が用いられることもあります。

 

問1（2）

（答）ウ

教科書に書かれている内容です。

こういう問題に対応できるよう、教科書も必ず2〜3読してください。

 

問1（3）

（答）①：水酸化ナトリウム水溶液、②：ア

BTB溶液が青色に変化したことから、水溶液Pはアルカリ性の物質であることが分かります。

よって、水溶液Pは水酸化ナトリウム水溶液、水溶液Qは塩酸です。

 

問2（1）

（答）オ

試験管Bには水溶液P（水酸化ナトリウム水溶液）が入っています。

水酸化ナトリウムの化学式はNaOHで、水溶液中ではNa⁺（陽イオン）とOH^–（陰イオン）で電離しています。

塩酸の化学式はHClで、水溶液中ではH⁺（陽イオン）とCl^–（陰イオン）で電離しています。

試験管Bに水溶液Q（塩酸）を1回加えたとき、H⁺とOH^–（陰イオン）が反応してH₂Oが発生し、陰イオンが1つ減ります。

しかし、水溶液Q（塩酸）を1回加えたとき、Cl^–（陰イオン）が1つ増えるので、全体としては陰イオンの数に変化はありません。

中和するまで、陰イオンの数は変化しません。

表より、試験管Bではマグネシウムが溶けているので、水溶液Q（塩酸）を5cm3加えたとき、酸性になっています。

中和してから水溶液Q（塩酸）を加えると、Cl^–（陰イオン）が増えていきます。

以上から、答えは選択肢オとなります。

 

問2（2）

（答）オ

試験管Eではマグネシウムが溶けなかったので、中和しており、H⁺の数はゼロです。

これから、試験管Aでは塩酸が4cm³含まれているといえます。

以上から、5cmの水溶液Q（塩酸）のH⁺の数（N₃）が一番多く、次に試験管A（N₁）、最後に試験管E（N₂）と成るので、答えは選択肢オとなります。

 

問2（3）

（答）0.09g

試験管Pでは中和していますが、試験管Dでは塩酸が1cm³多くマグネシウムは0.02g溶けています。

このように考えて表にまとめます。

試験管	余分なHCl(cm3)	反応するMg(g)
D	1	0.02
C	2	0.05(+0.03)
B	3	0.08(+0.03)
A	4	0.11(+0.03)

試験管Aではマグネシウムが0.11g溶けます。

すでにマグネシウムが0.1g溶けているので、あと0.01g溶かすことができるので、マグネシウムを0.10gをさらに加えると、残ったマグネシウムの質量は0.09gとなります。

大問4　動物の生活と生物の変遷（生物分野・中2）

 

 

問1（1）

（答）①：イ、②：イ

反射のはなしをしています。

反射は刺激の電気信号が大脳を通らず、意識してコントロールすることができません。

目の場合、明るい場所では虹彩が広がりひとみが小さくなり、暗い場所では虹彩が縮みひとみが大きくなります。

 

問1（2）

選択肢ア、イ、エは刺激の電気信号が大脳を通っていますが、選択肢ウは信号が大脳を通っていません。

 

問2（1）

（答）①鼓膜、②うずまき管、部分：D

単なる知識問題です。

音の刺激は、鼓膜により気体の振動が固体の振動に変換され、耳小骨で振動が増幅され、うずまき管で固体の振動が液体（リンパ液）の振動に変換され、うずまき管の中にある聴細胞がリンパ液の振動を受けとり、聴神経が刺激され大脳に電気信号として伝えられます。

図4において、Aは外耳、Bは耳小骨、Dはうずまき管、Cは聴神経です。

この他、体の回転を感じる半規管についても押さえてください。

 

問2（2）

（答）

短くなった時間：0.34秒

理由：ウ

表の計測時間は、太郎さんと花子さんが大脳で音を感知するのにかかった時間です。

1回目と5回目を比較すると、計測時間が0.68秒（1.49秒-0.81秒）短くなっています。

問題文で「刺激に対して反応するまでの時間に個人差はなく、疲労による影響は無視できるものとする」と書かれているので、1人当たり0.34秒短くなると考えることができます。

 

問2（2）

（答）1回目：エ、2回目：ウ

表の値を使って計算します。

・1回目

太郎さんと花子さんは続けて実験を行っているので、太郎さんと花子さんの計測時間は0.81秒です。

AさんとBさんは初めて実験を行うので、AさんとBさんの計測時間は1.49秒です。

よって、4人の計測時間は2.30秒（0.81秒＋1.49秒）となります。

・5回目

太郎さんと花子さんは続けて実験を行っているので、太郎さんと花子さんの計測時間は0.81秒です。

AさんとBさんの計測時間は、5回目の計測時間である0.81秒です。

よって、4人の計測時間は1.62秒（0.81秒＋0.81秒）となります。

大問5　身のまわりの現象（物理分野・中1）

 

 

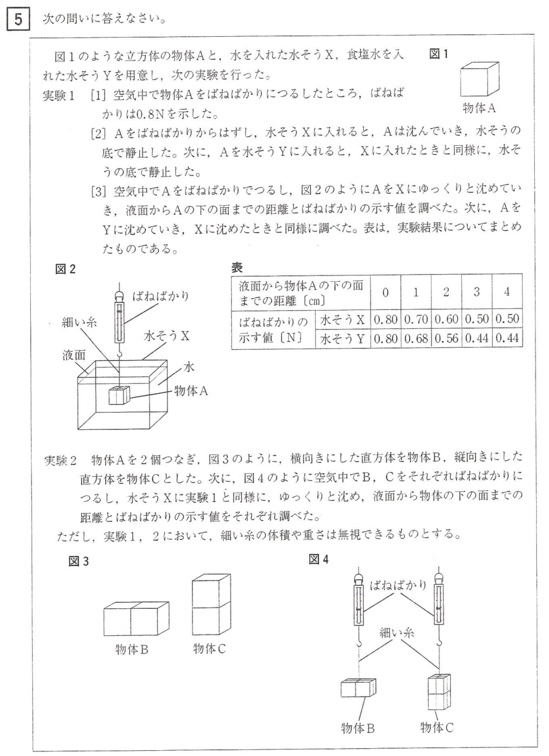
問1（1）

（答）①0.8、②0.24

①

重力は、地球上では場所によらず一定の値となります。

実験1[1]より、物体に働く重力の大きさは0.8Nと分かります。

②

表より、水そうYにAを沈め液面からAの下の面までの距離が2cmとなったとき、ばねばかりの示す値が0.56Nとなったことから、0.24N（0.8N-0.56N）の浮力が働いたことが分かります。

浮力は物体が押しのけた液体の重さです。

食塩水は水より密度（g/cm³）が大きく、同一体積では食塩水は水より質量が大きくなるため、浮力は密度が大きい食塩水のほうが大きくなります。

 

問1（2）

（答）27cm³

表より、液面から物体Aの下の面までの距離が3cmのとき、ばねばかりの示す値が変化せず浮力が一定となるので、物体Aの高さは3cmと分かります。

物体Aは立方体なので、辺の長さはすべて3cmです。

よって立方体の体積は27cm³（3cm×3cm×3cm）となります。

※

表より、物体Aが水槽に完全に沈んだとき、物体Aにかかる浮力の大きさは0.80N-0.50N＝0.30Nです。

仮に問題文に、以下の条件が与えられた場合、物体Aの体積は30cm³ともいえてしまいます。

仮定①　100gの物体にかかる重力の大きさを1Nとする（重力加速度、正確には0.98N）

仮定②　水の密度を1g/cm³とする（4℃の水の密度）

計算過程　0.30N×100g/N÷1g/cm³＝30cm³

しかし、問題文にこれらの仮定が与えられていないので、確実に言えることとして、上記の解説のとおりとなります。

 

 

問1（3）

（答）水:食塩水＝5:6

浮力は物体が押しのけた液体の重さです。

表より、液面から物体Aの下の面までの距離が3cmのとき、ばねばかりの示す値が変化せず浮力が一定となっています。

水を入れた水そうXの浮力は0.3N、食塩水のほうがを入れた水そうYの浮力は0.36Nです。

ここで、100gの物体に働く重力の大きさは1N（または0.98N）より、質量比は以下のようになります。

質量比=0.3N/(1N/100g):0.36N/(1N/100g)=0.30:0.36=30:36=5:6

 

問1（4）

（答）①1.6、②1

①

3力の釣り合い、かつ開く角度が同じ60°なので、力は以下のように正三角形のかたちで釣り合います。

 

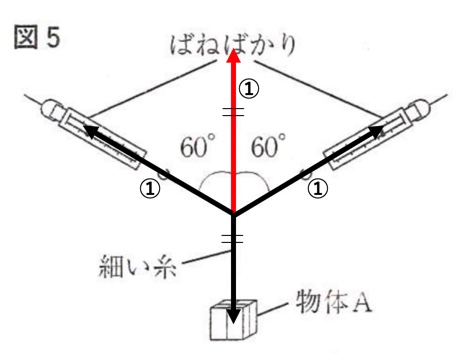
正三角形なので、各ばねばかりが示す値は、物体Aの重力である0.8Nです。

2つのばねばかり合わせて1.6Nになります。

この問題は3力の釣り合いの一番簡単なバージョンです。

正答率が低く、大手塾で「超難問」と評されていますが、『塾技 理科80』をやっていれば、瞬殺できる問題です。

本州の公立・私立高校では、これより難しい問題が普通に出題されています。

 

②

液面から物体Aの下の面までの距離が6cmのとき、物体Aは水そうにすべて沈んでいるので、表より物体Aが糸を引く力は0.50Nです。

物体Aが糸を引く力0.50Nが、各ばねばかりが示す値となるので、2つ合わせて1Nとなります。

 

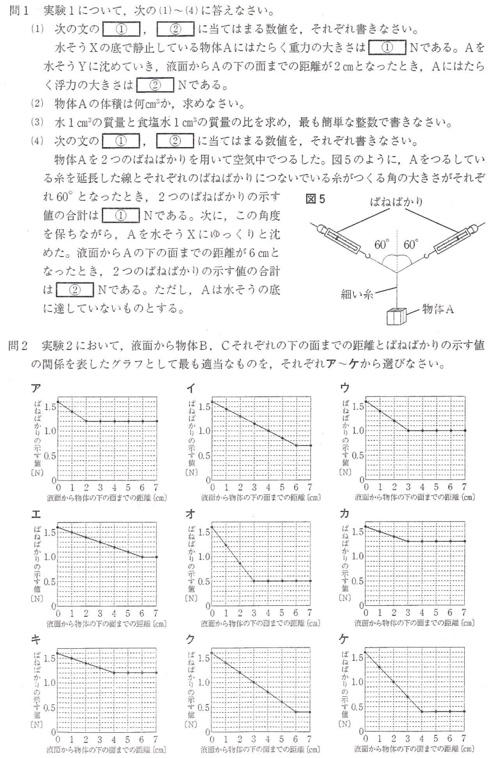
問2

（答）B：ウ、C：エ

・B

物体Bの高さは3cmより、液面から物体までの距離が3cm以上になると浮力が増えず、ばねばかりの示す値が一定になります。

物体Bの体積は物体Aの2倍なので、浮力の大きさも2倍となります。

表より、浮力の大きさは0.6N（0.3N×2）となります。

物体Bの重さは物体Aの2倍なので、重さは1.6N（0.8N×2）です。

以上より、液面から物体までの距離が3cm以上のとき、ばねばかりの示す値は1.0N（1.6N-0.6N）となるので、答えは選択肢ウとなります。

・C

物体Cの高さは6cmより、液面から物体までの距離が6cm以上になると浮力が増えず、ばねばかりの示す値が一定になります。

物体Cの体積は物体Aの2倍なので、浮力の大きさも2倍となります。

表より、浮力の大きさは0.6N（0.3N×2）となります。

物体Cの重さは物体Aの2倍なので、重さは1.6N（0.8N×2）です。

以上より、液面から物体までの距離が6cm以上のとき、ばねばかりの示す値は1.0N（1.6N-0.6N）となるので、答えは選択肢エとなります。