こんにちは、個別指導塾まさです。
今回は、2019年（平成31年）に行われた北海道公立高校入試の数学の過去問を解説していきます。
＞＞2020年の北海道公立高校入試「数学」の過去問と詳しい解説
＞＞2018年の北海道公立高校入試「数学」の過去問と詳しい解説
＞＞【最新版】北海道の公立・私立高校受験対策おすすめ問題集（道コンSS・高校別）と差がつく正しい使い方
オンライン個別指導塾と家庭教師をやっています。北大院卒、指導経験20年以上。当塾は中上位高校志望の子が多いですが、勉強が苦手な子も多数在籍しています。今の学力は不問ですので、気軽にお申し込みください。授業料は1回70分 3,000円〜です。
＞＞教師紹介・料金・授業内容
＞＞体験授業かんたんお申し込み
＞＞お問い合わせ
総評：非常に易しい
2019年の数学の平均点は、学校裁量問題合格者が40.1点（昨年は31.5点）と昨年と比較して9点もアップしました。
実際に問題を見ると、基本問題だらけで、とても学校裁量問題とは言えないレベルです。
学校のワークを完全に吸収できていれば、50点以上は取れるでしょう。
※学校のワークを完全に吸収するのはかなり難しい。
札幌東・西・南・北高校志願者は満点、旭丘や国際情報志願者は50点以上を狙って欲しいところです。
大問1 簡単な計算問題（学校標準問題）
解説
問1
（1）出来ないとマズいです。
（2）割り算はかけ算（逆数）にして計算です。総合ABCでもよく出題される問題です。
（3）√3で因数分解すると簡単に解けます。
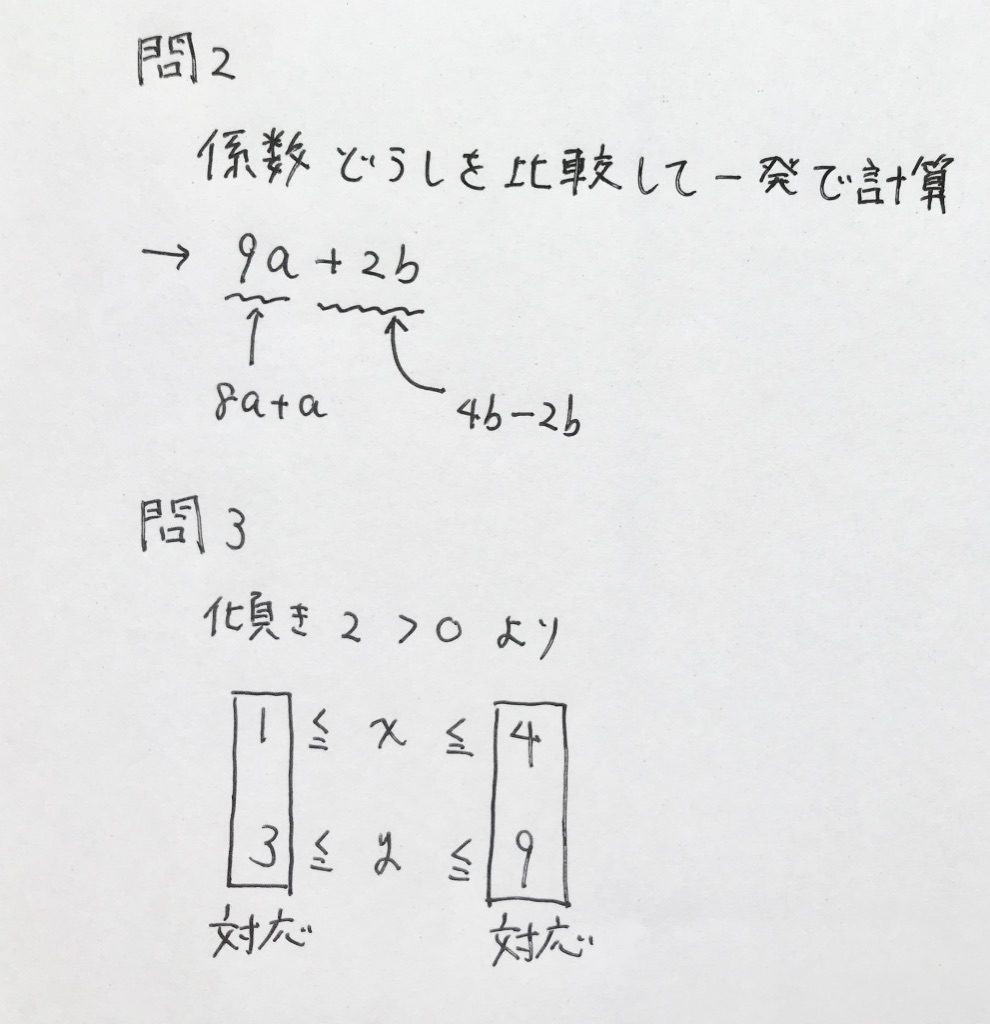
問2
中1の問題です。
通常の計算手順は、カッコを外す→同類項でまとめる→計算する、です。
しかしそれだと時間がかかるので、係数どうしを比較して一発で暗算できるようになってください。
問3
x=1のときy=3、x=4のときy=9から、yの変域が求まります。
『塾技 数学100』の知識があれば瞬殺できる問題です。
傾きが正なので、xの変域の最小値がyの変域の最小値に、xの変域の最大値がyの変域の最大値に対応します。
問4
代表値（平均値、最頻値、中央値）のひとつ、最頻値を求める問題です。
最頻値とは、最も大きい度数の階級の階級値です。
資料を見ると、「25回」が最も多くあり、その数が3つなので度数は3、このときの階級値は25なので、最頻値は25です。
度数分布表が与えられている方が代表値を算出しやすいと、私は思います。
問5
三角形が直角三角形であるためには、三平方の定理が成り立つ必要があります。
このとき、3つの辺の中で最も長い辺が斜辺になります。
また三平方の定理と合わせて、直角三角形の三辺比の知識も身につけましょう。
とくに、以下の4つの直角三角形の三辺比は絶対に抑えてください。
・「1：1：√2」（直角二等辺三角形の三辺比）
・「1：2：√3」（鋭角が60°、30°の直角三角形）
・「3：4：5」
・「5：12：13」
問6
学校のワークのAレベル（易しい問題）によくある問題です。
線分を移動して相似な三角形をつくり、比例式を立てるのが一般的な手順です。
それでも良いのですが、左側の辺の比が4:8=1:2なので、xは3cmを2倍すればすぐに計算できます。
解答例
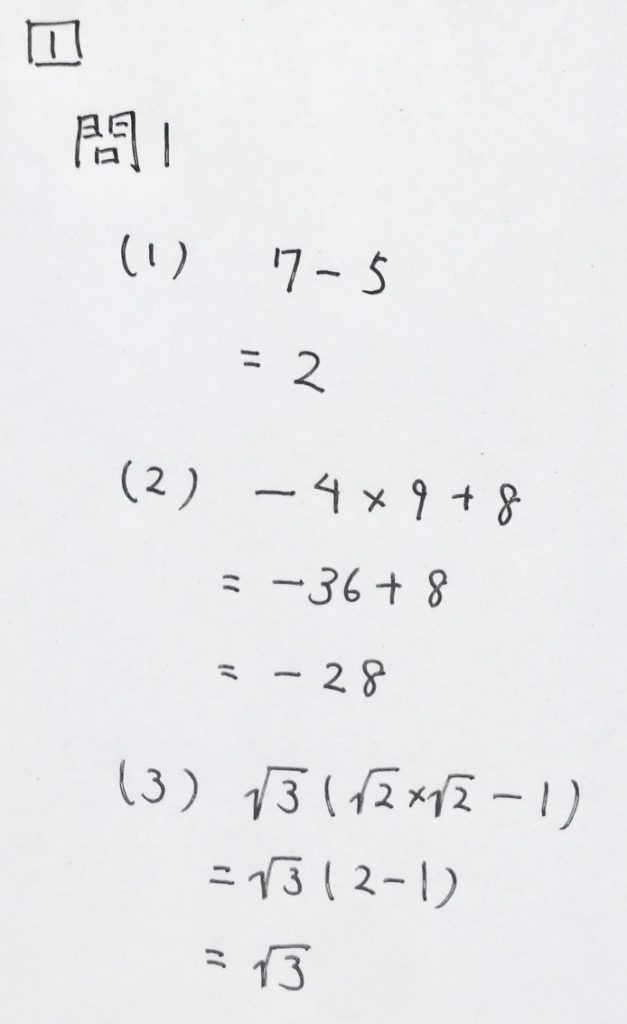
大問1 計算問題（学校裁量問題）
解説
問1
学校のワークのBレベル（標準レベルの問題）によくある問題です。
2でくくる過程を飛ばして、一発で計算できるよう努力してください。
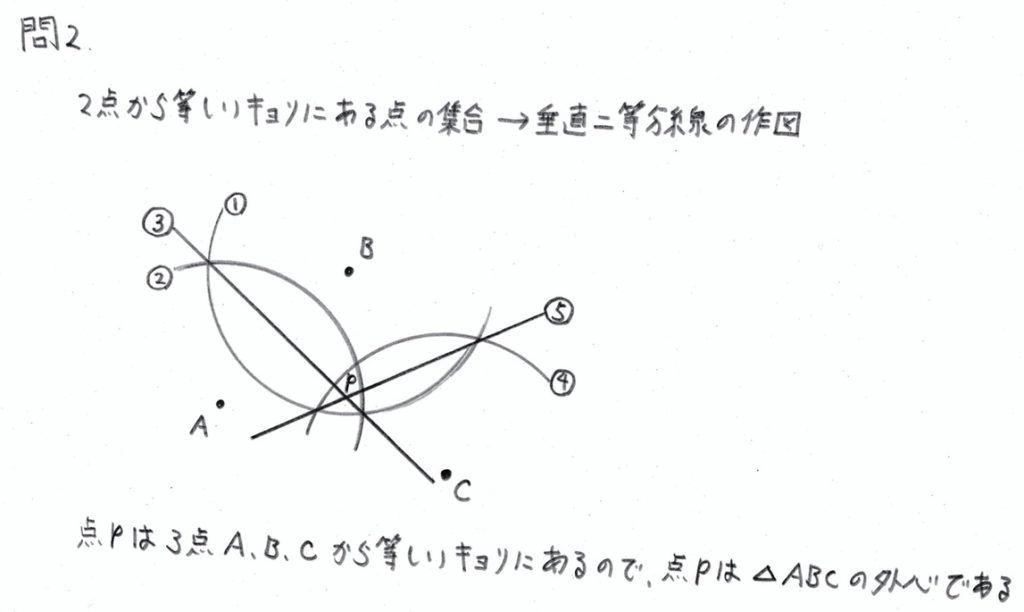
問2
作図の問題です。
2点から等しい距離にある点の集合なので、垂直二等分線を作図します。
ちなみに、2辺から等しい距離にある点の集合の場合は、角の二等分線を作図します。
学校のワークのAレベル（易しい問題）によくある問題です。
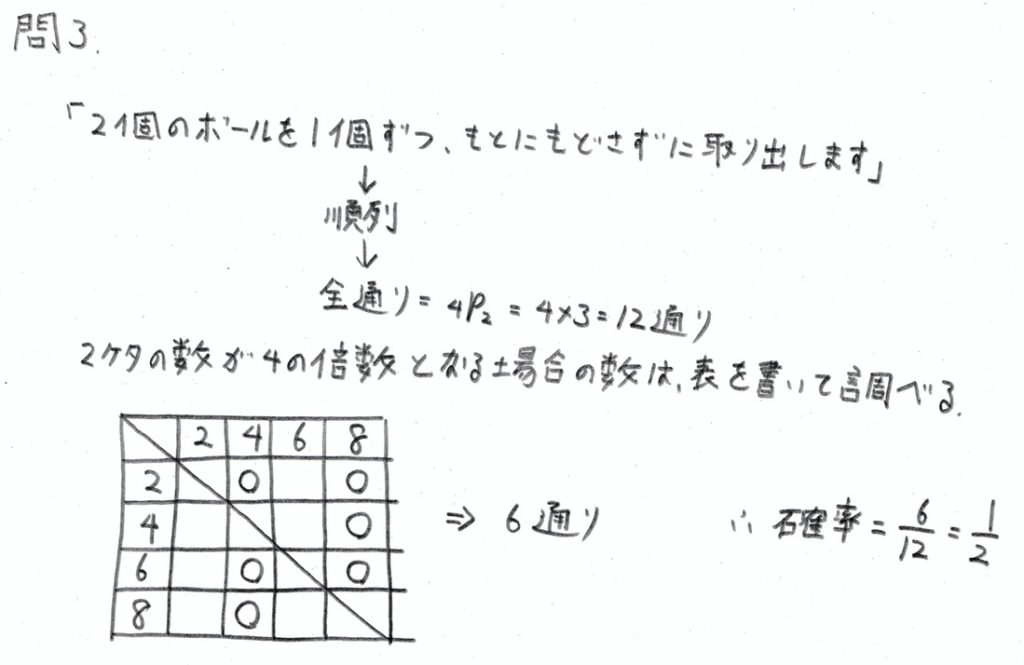
問3
確率の問題です。
樹形図ではなく表でやると速く解けます。
学校のワークのBレベル（標準レベルの問題）の問題です。
問4
図形の計算問題です。
柱体の体積＝（底面積）×（高さ）、高さ＝hとおいて方程式を立てて計算してhを求めます。
なお、錐体の体積＝（底面積）×（高さ）×1/3、です。
「錐体は上に尖っており、柱体より体積が減るので1/3をかける」と覚えるとよいでしょう。
学校のワークのBレベル（標準レベルの問題）の問題です。
解答例
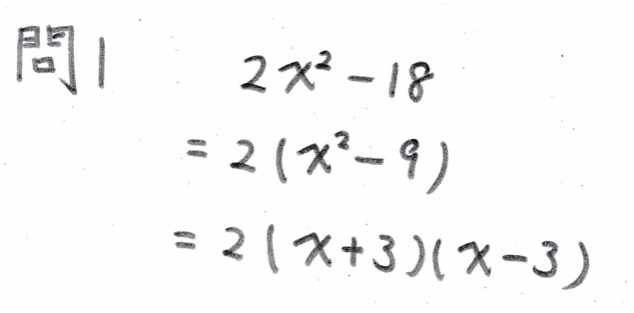
大問2 穴埋め問題（学校裁量問題）
解説
問1
ア 1列の数の和がaで、9つのマスには3列あるので、9つのマスの合計は3倍して3aになります。
イ 4列あるので、9つのマスの合計は4倍して4aになります。
ウ イの計算では、中央のますを3回ダブって計算しているので、9つのマスの合計を求めるとき、中央のますを3回引く必要があります。
問2
本セットの中で、最も難しい問題だと感じました。
解き方については、解答例をご参照ください。
解答例
※青枠の部分は、個別指導塾まさの生徒限定の情報で、入試数学を攻略するうえで知っていると有利になるポイントです。
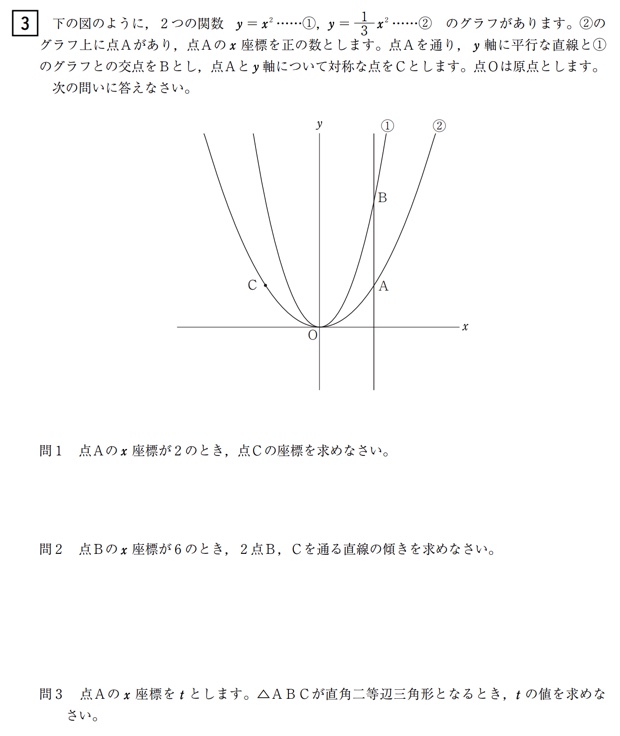
大問3 関数の問題（学校裁量問題）
解説
問1
学校のワークのAレベル（易しい問題）の問題です。
点Cは点Aとy軸に対して対称な点なので、点Aのx座標の符号が逆になります。
問2
学校のワークのBレベル（標準レベルの問題）の問題です。
点Bの座標を求める→点Aの座標を求める→点Cの座標を求める→傾きを求める
の手順で解けます。
問3
学校のワークのBレベル（標準レベルの問題）の問題です。
△ABCが直角二等辺三角形なので、AB＝ACとなります。
解く手順は、以下のとおりです。
点Aの座標をtで表す→点Bの座標をtで表す→点Cの座標をtで表す→線分ABと線分ACの長さを求める→方程式を立ててtを求める→t>0よりtの値を決定する
解答例
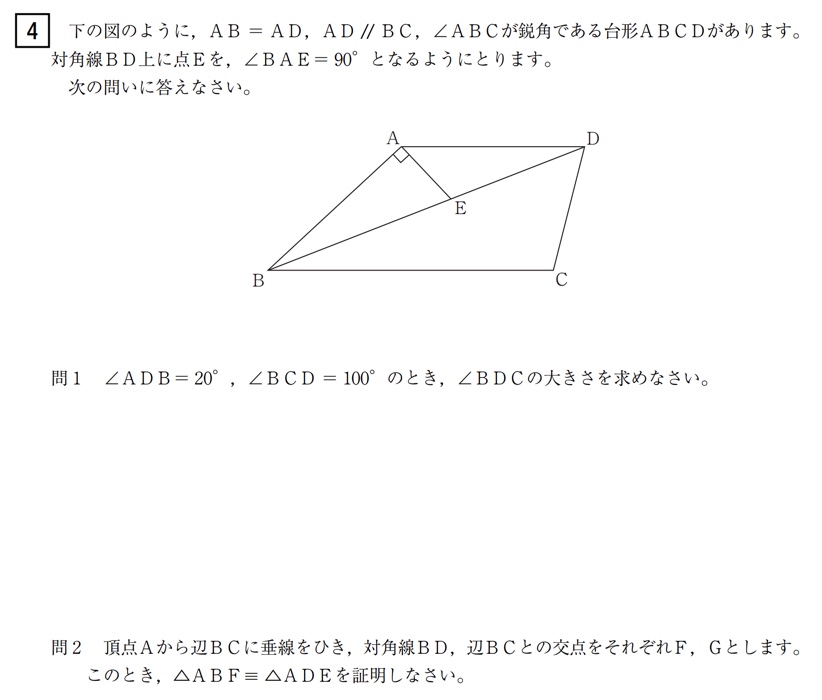
大問4 図形問題（学校裁量問題）
解説
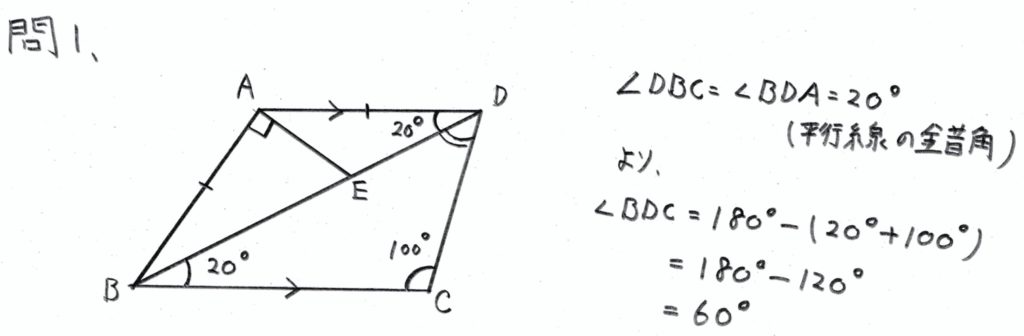
問1
学校のワークのAレベル（易しい問題）の問題です。
解答例参照。
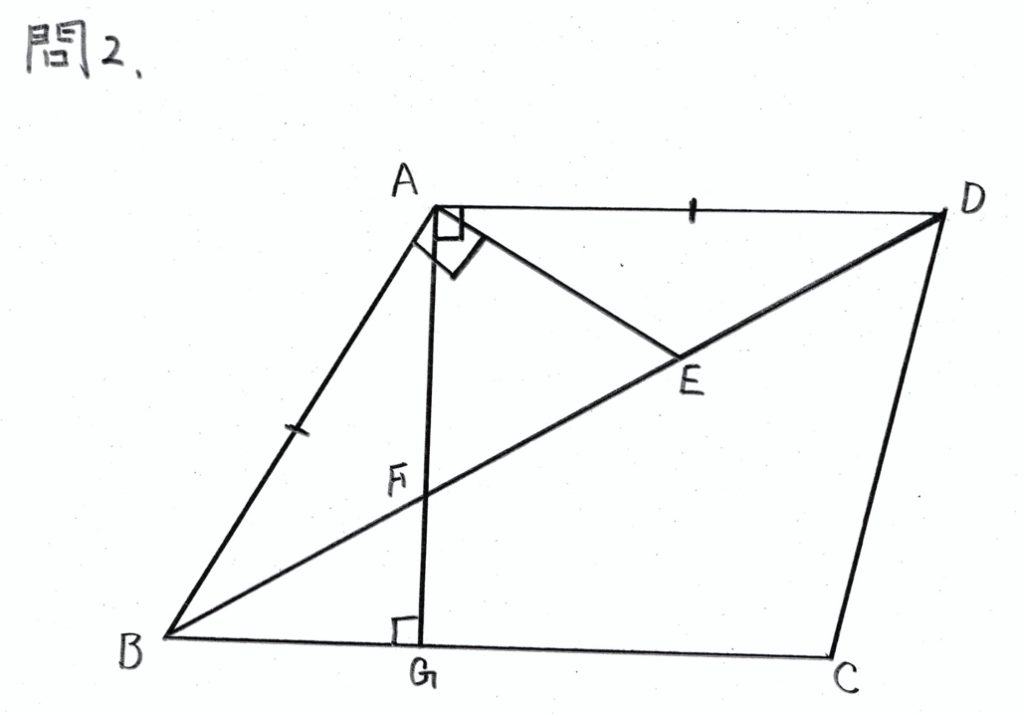
問2
学校のワークのBレベル（標準レベルの問題）の問題です。
証明問題の典型的な問題です。
解き方は、解答例をご参照ください。
解答例
※青枠の部分は、個別指導塾まさの生徒限定の情報で、入試数学を攻略するうえで知っていると有利になるポイントです。
大問5 学校裁量問題
解説
問1（1）
学校のワークのAレベル（易しい問題）の問題です。
直角三角形の「5：12：13」の三辺比を知っていれば、瞬殺できます。
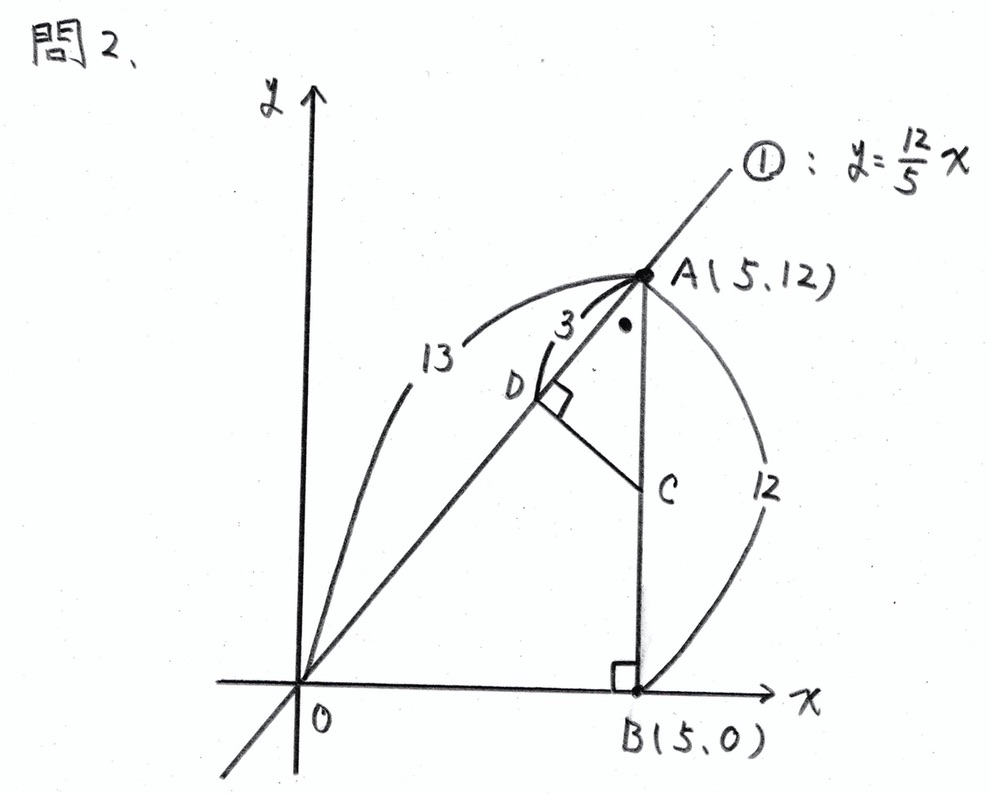
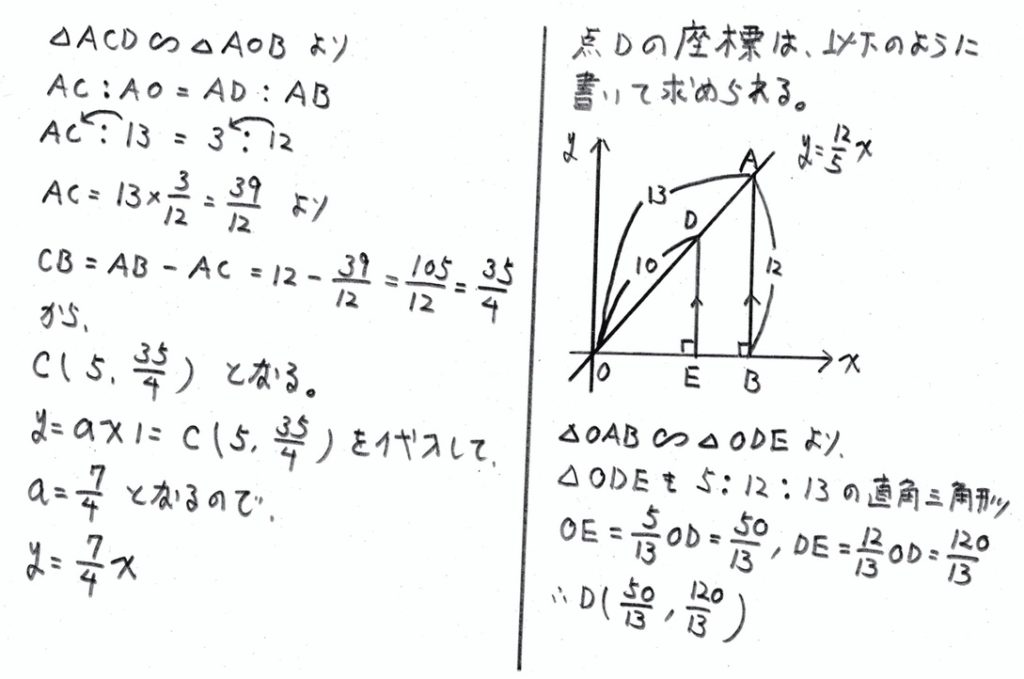
問1（2）
学校のワークのBレベル（標準レベルの問題）の問題です。
以下の手順で解きます。
相似な三角形を探す→比例式を立てて線分ACの長さを求める→点Cの座標を求める→一次関数 y=axの式に点Cの座標の値を代入してaを求める または 点Cの座標から傾きを求める
問2（1）
学校のワークのAレベル（易しい問題）の問題です。
代表値（平均値、最頻値、中央値）のひとつ、平均値の計算方法を抑えていれば瞬殺できます。
問2（2）
学校のワークのBレベル（標準レベルの問題）の問題です。
不明な値が2つあるので、連立方程式を立てます。
この場合、度数の合計値と（度数）×（階級値）の合計値に着目して立式します。
問2（3）
学校のワークのBレベル（標準レベルの問題）の問題です。
問題で「30人の（度数）×（階級値）の合計は、」と誘導してくれているので、誘導に従って機械的に計算すれば簡単に解けます。
以下の手順で解きます。
平均値から30人の（度数）×（階級値）の合計を求める→元の（度数）×（階級値）の合計との差分を求める→（度数）×（階級値）の差分が150、度数が6から階級値を求める→階級を求める。
解答例
※青枠の部分は、個別指導塾まさの生徒限定の情報で、入試数学を攻略するうえで知っていると有利になるポイントです。
