【2017年】北海道公立高校入試「理科」の過去問を詳しく解説。使える画像付き！！

 

＞＞的中率60%以上！今年度の北海道公立高校入試「理科」はここが狙われる！家庭教師のそらの予想出題分野

 

北海道公立高校入試過去問はこちら

★過去問

★模擬テストとリスニング対策

※模擬テストは1教科のみ表示。Amazonなどでは5教科すべて販売されています。

大問1　小問集合

 

 

問1

（1）

（答）水素

 

（2）

（答）等速直線運動

等速直線運動と等加速度運動の違いをきちんと押さえておきましょう。

等速直線運動は、時間が増えても一定の速さで運動で、物体の進行方向に力が働かない。

等加速度運動は、時間が増えると一定の割合で速さが増えていく運動で、物体の進行方向に力が働いている。

という感じです。

 

（3）

（答）反射

反射では刺激の信号が大脳を通りません。

刺激の流れは、感覚器官→感覚神経→脊髄（背中側）→脊髄（腹側）→運動神経→運動器官、です。

一方で、大脳でも刺激を検知していることに注意してください。

刺激の流れは、感覚器官→感覚神経→脊髄（背中側）→大脳、です。

 

（4）

（答）還元

「鉄鉱石から鉄」を読んだ段階で、「酸化鉄の還元」と連想できるのが理想です。

「酸化物から酸素がうばわれる」と書かれているので、答えは「還元」です。

 

（5）

（答）栄養

「無性生殖」「ジャガイモやサツマイモ」ときたら、「栄養生殖」しかありません。

無性生殖のメリット、無性生殖と有性生殖の違いについて、きちんと押さえてください。

 

（6）

（答）気団

シベリア気団、オホーツク海気団、小笠原気団について、勢力を強める季節、気圧配置、衛星画像、季節風の向き、前線など、体系的に勉強してください。

 

（7）

（答）放射線

 

問2

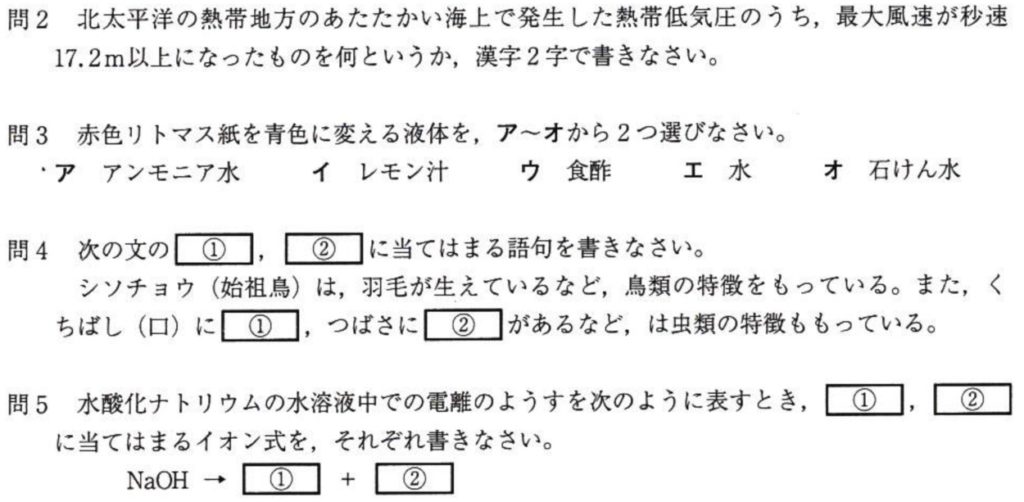
（答）台風

「熱帯低気圧のうち、最大風速が秒速17.2m/s以上になったもの」と聞かれたら、台風です。

台風の構造、台風の進路（小笠原気団の縁に沿って進み偏西風で東寄りに進路を変える）、風向の変化、風力の変化を押さえておいてください。

 

問3

（答）ア、オ

酸性の水溶液を選べと言っています。

アのアンモニア水は、アルカリ性（水に溶けるとOH^–を放出するアルカリ）

イのレモン汁は、酸性（リトマス紙 青→赤）

ウの食酢は、酸性

エの水は、中性

オの石けん水は、アルカリ性

です。

 

問4

（答）①歯、②つめ

始祖鳥は、鳥類（羽毛、くちばし、つばさ）とは虫類（歯、爪、長い尾骨）の特徴を併せ持っています。

 

問5

（答）①Na⁺、②OH^–

電離式のはなしです。

水酸化ナトリウム（NaOH）の電離式の他に、水酸化バリウム（BaSO₄）、塩酸（HCl）、硫酸（H₂SO₄）、塩化銅（CuCl₂）の電離式もすぐに書けるようになってください。

 

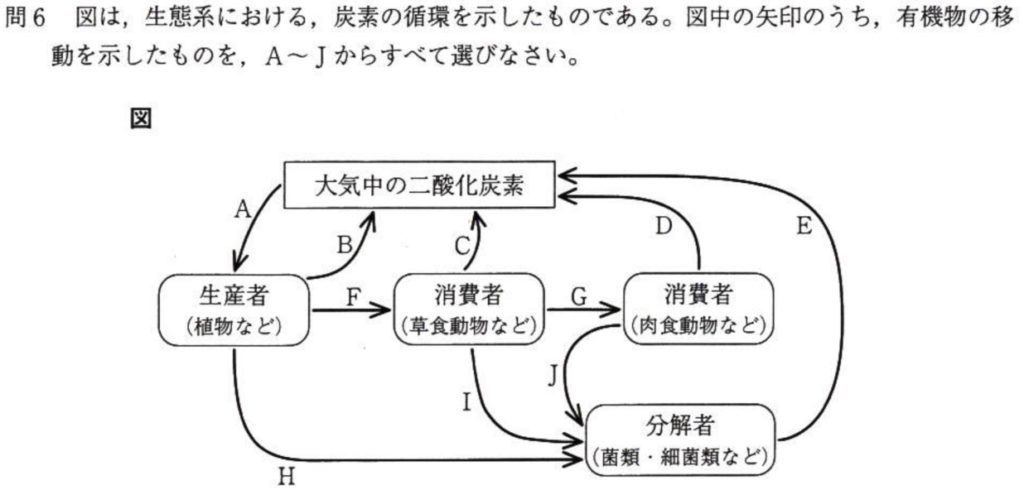
問6

（答）F、G、H、I、J

有機物の流れを問われているので、解答のとおりです。

二酸化炭素の流れについて、生産者（植物）のみ両方向の矢印になっている理由は、植物は呼吸と光合成の両方を行っているからです。

 

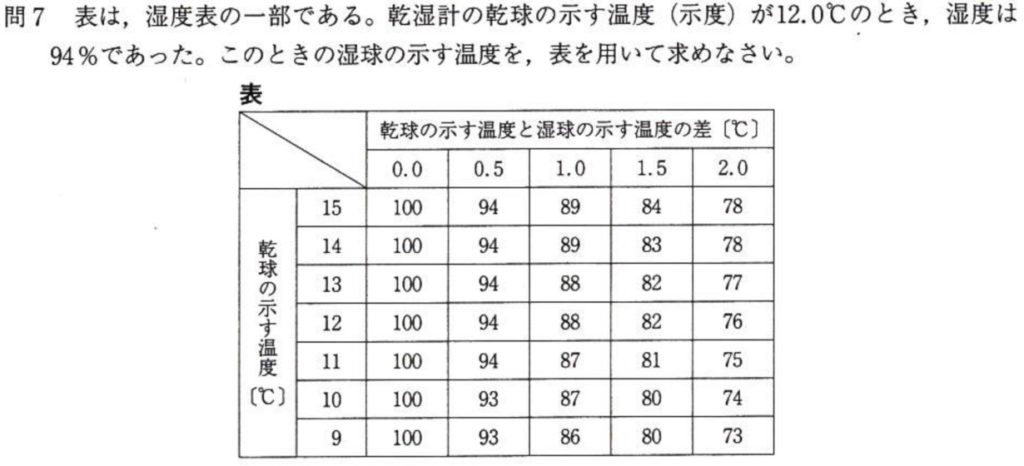
問7

（答）11.5℃

乾球の温度（示度）が12℃、湿度が94％を表から探すと、乾球と湿球の温度差が0.5℃と分かります。

湿球は気化熱により乾球より温度が低いので、湿球の温度（示度）は11.5℃になります。

 

問8

（答）30km

数学の問題です。

単位に着目して計算すれば終わりです。

150km/h×12/60h=150km/h×1/5h=30km

大問2　状態変化（化学分野・中1）

 

 

問1

（答）①イ、②エ

①：

物質P（水）、Q（ロウ）が固体になったときに体積が変化したのは、粒子（分子）の運動が変化したからです。

固体のとき、粒子は集合して細かく振動しています。液体のとき、粒子はくっついたり離れたりして動いています。

以上から、答えは粒子の「集まり方と運動のようす」になります。

②：

状態変化では、粒子の種類と数は変化しません。粒子の動きが変わるだけです。

化学変化では、分子（粒子）の種類と数が変化します。

以上から、答えは粒子の「種類と数」になります。

 

問2

（答）印まで水を加え、その水の体積をメスシリンダーではかる。

教科書に書かれている内容です。

時間があるときに、教科書も2〜3読しておきましょう。

 

問3

（答）物質P：0.91g/cm³、物質Q：0.82g/cm³

物質P：

実験[1]より、物質Pの質量は100g（ビーカー全体の質量140g − ビーカーの質量40g）、実験[1][4]と図より、物質Pの体積は110cm³です。

以上から、密度の単位g/cm³に従って以下のように計算します。

密度(g/cm³)=100g/110cm³=10g/11cm³=0.909･･･g/cm³≒0.91g/cm³

物質Pの体積は固体になったときに増加しているので、物質Pは水と分かります。

物質Q：

実験[1]より、物質Qの質量は72g（ビーカー全体の質量112g − ビーカーの質量40g）、実験[1][4]と図より、物質Qの体積は88cm³です。

以上から、密度の単位g/cm³に従って以下のように計算します。

密度(g/cm³)=72g/88cm³=9g/11cm³=0.818･･･g/cm³≒0.82g/cm³

物質Qの体積は固体になったときに減少しているので、物質Pはロウと分かります。

 

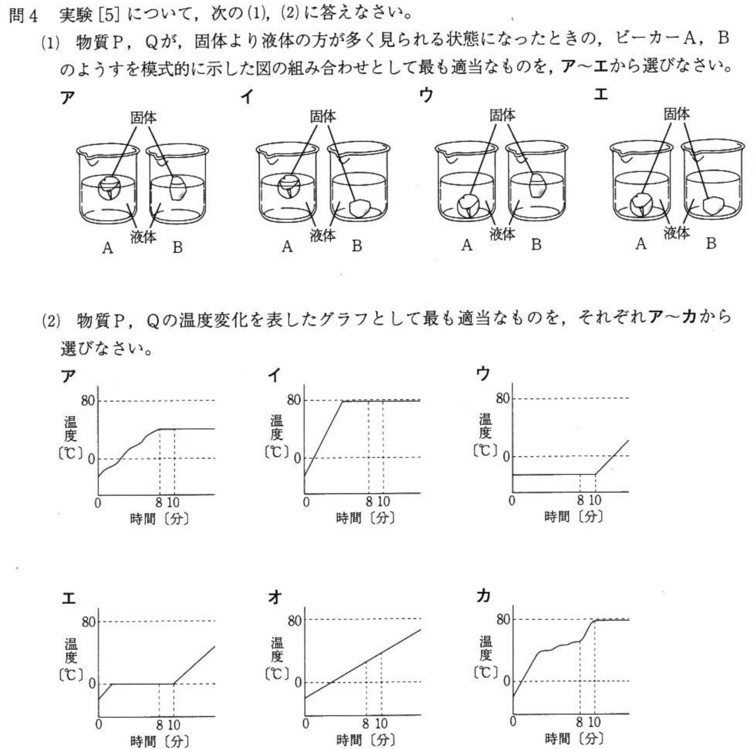
問4（1）

（答）イ

問3より、物質P（ビーカーA）は水、物質Q（ビーカーB）はロウと分かります。

水は、液体（水）→固体（氷）に状態変化したとき、体積が増加するので密度が減少します。なので、氷は水に浮きます。

水以外の物質は、液体→固体に状態変化したとき、体積が減少するので密度が増加します。なので、固体は液体に沈みます。

 

問4（2）

（答）物質P：エ、物質Q：カ

物質P：

物質Pは水なので、純粋な物質です。

純粋な物質の融点と沸点は決まっており、グラフは直線的な形になります。

実験[5]より10分後に全て液体になったことから、10分を境に温度が0℃から上がります。

以上から、物質Pの答えはエと分かります。

物質Q：

物質Qはロウなので、混合物です。

混合物の融点と沸点は一定ではなく、グラフは曲線的な形になります。

実験[5]より8分後に全て液体になったことから、8分を境に温度が上がります。

以上から、物質Qの答えはカと分かります。

大問3　太陽と月（地学分野・中3）

 

問1（1）

（答）直接見ては

教科書に書かれている内容です。

時間があるときに、教科書も2〜3読しておきましょう。

 

問1（2）

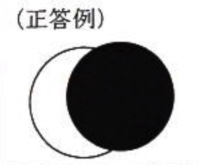
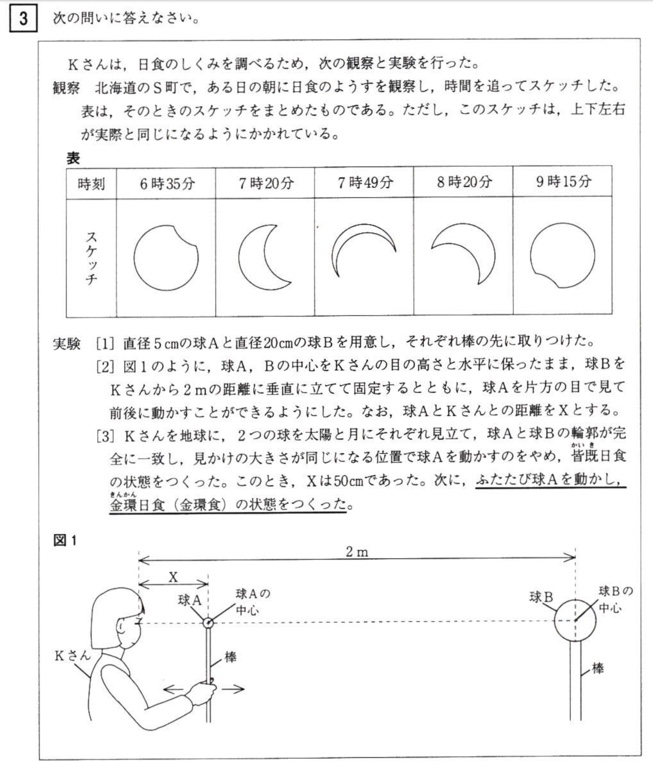
太陽と月が同じサイズになるように作図してください。

太陽と月が同じサイズになる理由は、太陽の直径は月の400倍であるが、地球からの距離も400倍であるため、地球上では太陽と月が同じサイズに見えるからです。

 

問1（3）

（答）①ア、②ア、③イ

①②

日食は、月が新月（月齢0）のときに起こります。

地球は西から東に自転しているため、1日でみたら月と太陽は東から西に動いて見えます（見かけの動き）。

日食が起こるとき、月が最初に天体上に現れるのは暗記しましょう。

天体上で真南の方向を見ると、月と太陽は東から西に動いて見えますが、月は西から東に1日12°公転しているため、見かけの動きの速さは太陽のほうが大きいです。

ゆえに太陽が月に追いついて、太陽の右（西）側が欠けて右（西）側から満ちていきます。

これが日食のメカニズムです。

月が満月（月齢15）のときに起こる月食のときは、地球の影を太陽と見立てて、日食と同じように考えると、月の左（東）側が欠けて左（西）側から満ちていくことが分かります。

③

月は西から東に1日12°公転しています。

地球も西から東に1日12°自転しています。

天体上で考えると分かりやすいですが、月が南中してから翌日同じ時刻に月は12°西から東にずれるので、12°分地球を自転させる必要があります。

つまり、月が南中してから次に南中する時刻は遅くなります。

地球は1日（24時間）360°、1時間で15°西から東に自転しているため、12°自転するのにかかる時間は48分（※）なので、48分遅くなります。

※60分：15°＝x：12°を解くと、x＝48分

 

問2（1）

（答）①イ、②イ、③ア

実験[1][2][3]より、皆既日食のときKさんと球A（月）までの距離は50cmです。

球A（月）と球B（太陽）の直径の比が4：1なので、皆既日食のときは、Kさんからの距離の比も4：1になります。

Kさんと球B（太陽）までの距離は2m（200cm）なので、Kさんと球A（月）までの距離は4分の1倍の50cmとなるのです。

これで、球A（月）と球B（太陽）は、Kさんから見てちょうど同じ大きさにみえるので、球B（太陽）が球A（月）に隠されます。

金環日食のとき、月の外側に太陽の一部がはみ出します。

つまり、球A（月）は球B（太陽）より小さく見えます。

そうなるには、Kさんと球A（月）までの距離を50cmより大きくする必要があります。

 

問2（2）

（答）①4、②4、③152,000,000

①②

問2（1）の解説より、球B（太陽）の直径は球A（月）の4倍、Kさんと球B（太陽）までの距離は球A（月）までの距離の4倍です。

③

球A（月）と球B（太陽）の直径の比と、Kさんと球A（月）と球B（太陽）までの距離の比が等しいことに着目して、比例式を立てます。

3500km：140万km=38万km：x

140万km/3500km=400

より

x=400×38万km=15200万km=152000000km

太陽の直径は月の400倍であるが、地球からの距離も400倍であることを知っていれば、簡単に解ける問題でした。

大問4　電流とその利用（物理分野・中2）

 

 

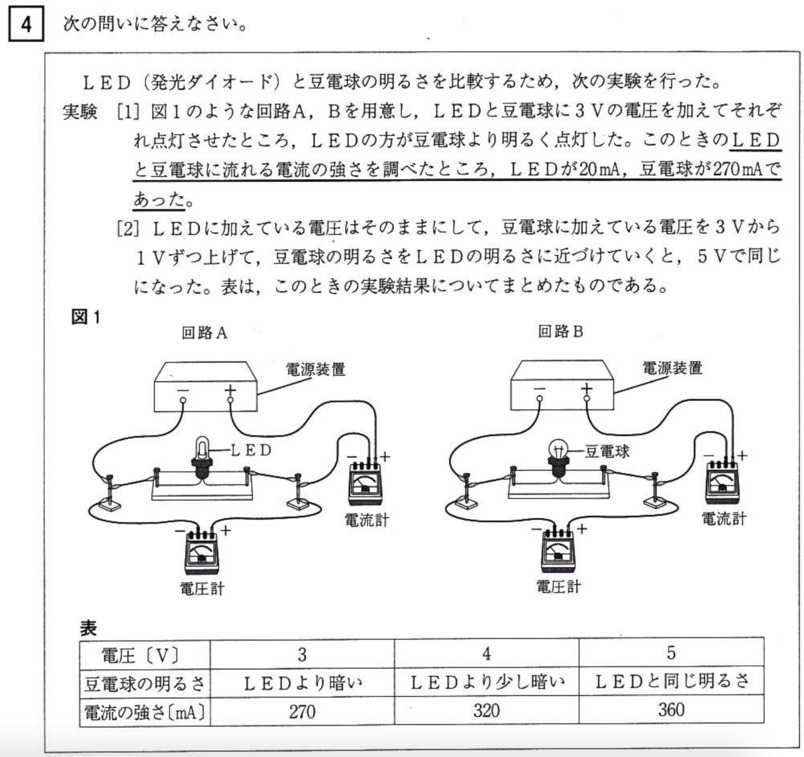
問1

（答）150Ω

オームの法則より

R=V/I=3V/20mA=3V/(20/1000A)=3×1000/20}Ω=3×50Ω=150Ω

 

問2

（答）①ア、②イ

電流計のマイナス端子には、回路を流れる電流が20mAと分かっているので50mAに接続します。回路を流れる電流が270mAと分かっているので500mAに接続します。

回路を流れる電流が不明のときは、5Aに接続します。

電圧計も同じようにして接続します。

電流計は直列に、電圧計は並列に接続することも合わせて覚えましょう。

 

問3

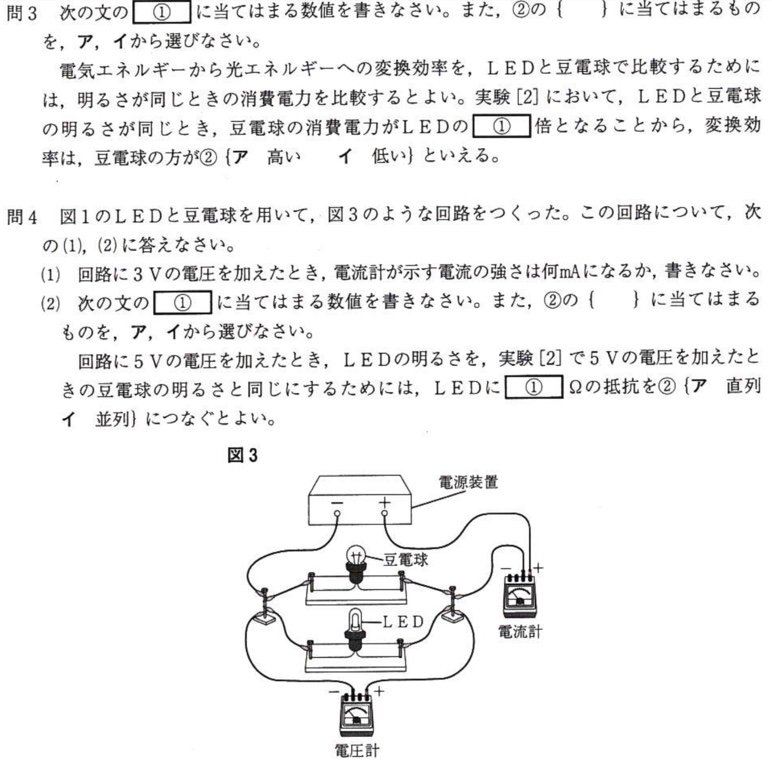
（答）①30、②イ

実験[2]のとき、

LEDの消費電力は

P(W)=P(J/s)=I×V=3V×20mA=60mW

豆電球の消費電力は

P(W)=P(J/s)=I×V=5V×360mA=1800mW

豆電球の消費電力はLEDの

1800mW/60mW}=30倍

1秒あたりで見ると、同じ明るさにするのに豆電球はLEDの30倍の電気エネルギーが必要で、投入した電気エネルギーの変換効率がLEDより低いことがわかります。

 

問4（1）

（答）290mA

実験[1]より、3Vの電圧を加えたとき、LEDには20mA、豆電球には270mAの電流が流れます。

図3は並列回路より、電流計が示す値は各抵抗の部分電流の和となるので、290mAとなります。

 

問4（2）

（答）①100、②ア

LEDの明るさを、実験[2]で5Vの電圧を加えたときの豆電球の明るさと同じにするには、LEDにかかる電圧を3Vにする必要があります。

しかし、図3の回路に5Vの電圧を加えたとき、並列回路より、LEDにかかる電圧は5Vになってしまいます。

ここで、直列回路の回路全体の電圧は、各抵抗の部分電圧の和になることに着目すると、電圧が2Vかかる抵抗をLEDに直列につなぐと、LEDにかかる電圧は3Vになります。

LEDにかかる電圧は3Vのとき、実験[1]よりLEDの電流は20mAになります。

LEDと抵抗は直列に接続しているので、抵抗に流れる電流も20mAになります。

オームの法則より、この抵抗の抵抗値は

R=V/I=2V/20mA=2V/(20/1000A)=2×1000/20Ω=100Ω

大問5　植物の生活と種類（生物分野・中1）

 

 

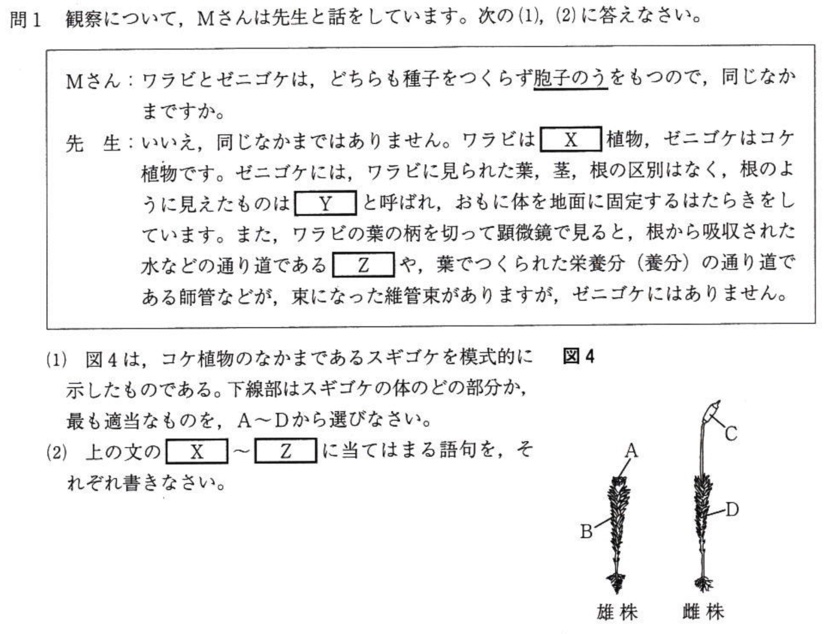
問1（1）

（答）C

コケ植物の仲間として、ゼニゴケとスギゴケの2つを覚えましょう。

なお、Cは胞子のうです。

胞子のうの場所は、ゼニゴケは雌株の雌器（図1では傘のようなもの）、スギゴケは雌株の先端にあります。

 

問1（2）

（答）X：シダ（植物）、Y：仮根、Z：道管

単なる知識問題です。

シダ植物とコケ植物の体のつくり、増え方（「胞子で増える」の知識だけではダメ）、シダ植物とコケ植物の相違点と類似点をしっかり押さえてください。

 

問2（1）

（答）①エ、②オ、③ウ

まず実験[1][2][3]の文章をよく読んで、蒸散が起こる場所を調べます。

実験[1]＝（葉の表、葉の裏、茎）

実験[2]＝（葉の裏、茎）

実験[3]＝（茎）

①

葉の表＝実験[1]−実験[2]＝（葉の表、葉の裏、茎）−（葉の裏、茎）

より、答えはエです。

②

葉の裏＝実験[2]−実験[3]＝（葉の裏、茎）−（茎）

より、答えはオです。

③

葉以外＝茎＝実験[3]

より、答えはウです。

 

問2（2）

（答）葉の表：0.2g、葉の裏：0.3g

まず、図3より、各実験で15分間に減少した水の量（蒸散量）を調べます。

実験[1]＝238.6g−238.0g＝0.6g

実験[2]＝242.4g−242.0g＝0.4g

実験[3]＝2マス減っているので0.1g

問2（1）より、

葉の表＝実験[1]−実験[2]＝0.6g−0.4g＝0.2g

葉の裏＝実験[2]−実験[3]＝0.4g−0.1g＝0.3g