埼玉県公立高校入試オススメ過去問題集
★過去問

★模擬テストとリスニング対策

※模擬テストは1教科のみ表示。Amazonなどでは5教科すべて販売されています。
大問1 小問集合

問1
解答:ウ
解説:
火成岩を選べばよいです。
ア:石灰岩は、堆積岩です。
イ:チャートは、堆積岩です。
ウ:正しい。
エ:砂岩は、堆積岩です。
問2
解答:ア
解説:
単純な知識問題なので、解説略。
問3
解答:エ
解説:
ア:イオン化傾向の大きさがZn>Cuなので、亜鉛が溶けて亜鉛イオンになり、電子が亜鉛板から銅板へ流れます。よって、正しい。
イ:イオン化傾向の大きさがZn>Cuなので、正しい。
ウ:電流が流れるにつれて、硫酸亜鉛水溶液では+の電気である亜鉛イオンが多く、硫酸銅水溶液では-の電気である硫酸イオンが多くなっていきます。このような電気の偏りをなくすため、セロハン膜を通じて、亜鉛イオンは硫酸亜鉛水溶液側へ、硫酸イオンは硫酸亜鉛水溶液側へ移動します。よって、正しい。
エ:亜鉛が溶けるので、亜鉛板は軽くなっていきます。銅板側では硫酸亜鉛水溶液の銅イオンが電子を受け取り銅になるため、銅板表面に銅が析出して重くなっていきます。よって、選択肢エが正解です。
問4
解答:ア
解説:
図3を正面から見て、磁界の向きがN極からS極(下から上)、電流の向きが左から右なので、力の向きは選択肢アです。
問5
解答:
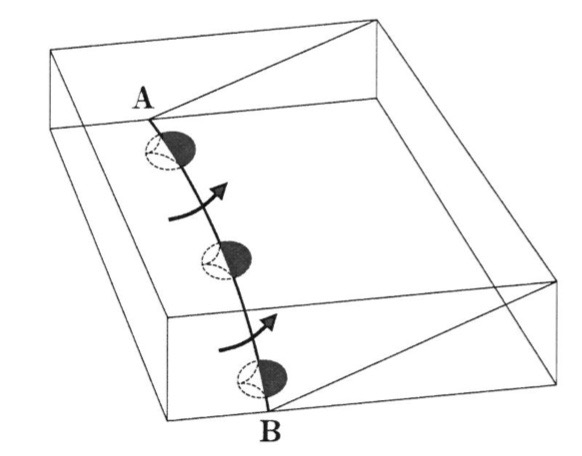
解説:
図4の線A-Bは、温暖前線を表しています。前線の進む向きが右側であるので、線A-Bの右側を塗りつぶします。
問6
解答:やく
解説:
単純な知識問題なので、解説略。
問7
解答:2H2+O2 → 2H2O
解説:
水素が燃焼すると水が生じるので、化学反応式を以下のように書きます。
H2+O2 → H2O
左辺の酸素原子は2個・右辺の酸素原子は1個なので、右辺の水分子を2倍します。
H2+O2 → 2H2O
左辺の水素原子は2個・右辺の水素原子は4個なので、左辺の水素原子を2倍します。
2H2+O2 → 2H2O
全ての原子を見たので、これで完了です。
問8
解答:全反射
解説:
光ファイバーは全反射を利用したもので、光を弱めることなく遠くに伝えることができます。
スポンサーリンク
大問2 太陽の日周運動と年周運動 ★問5が難
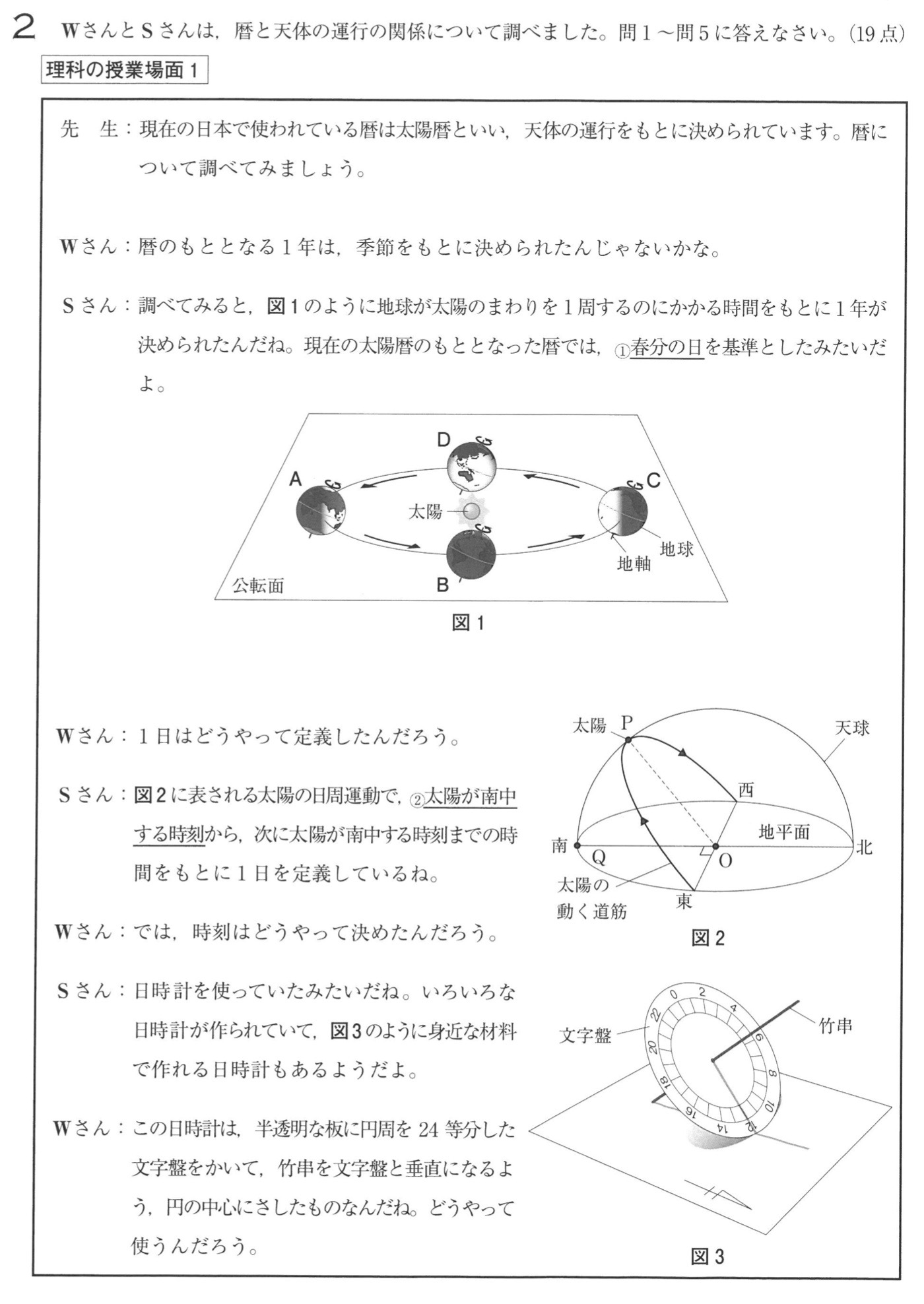
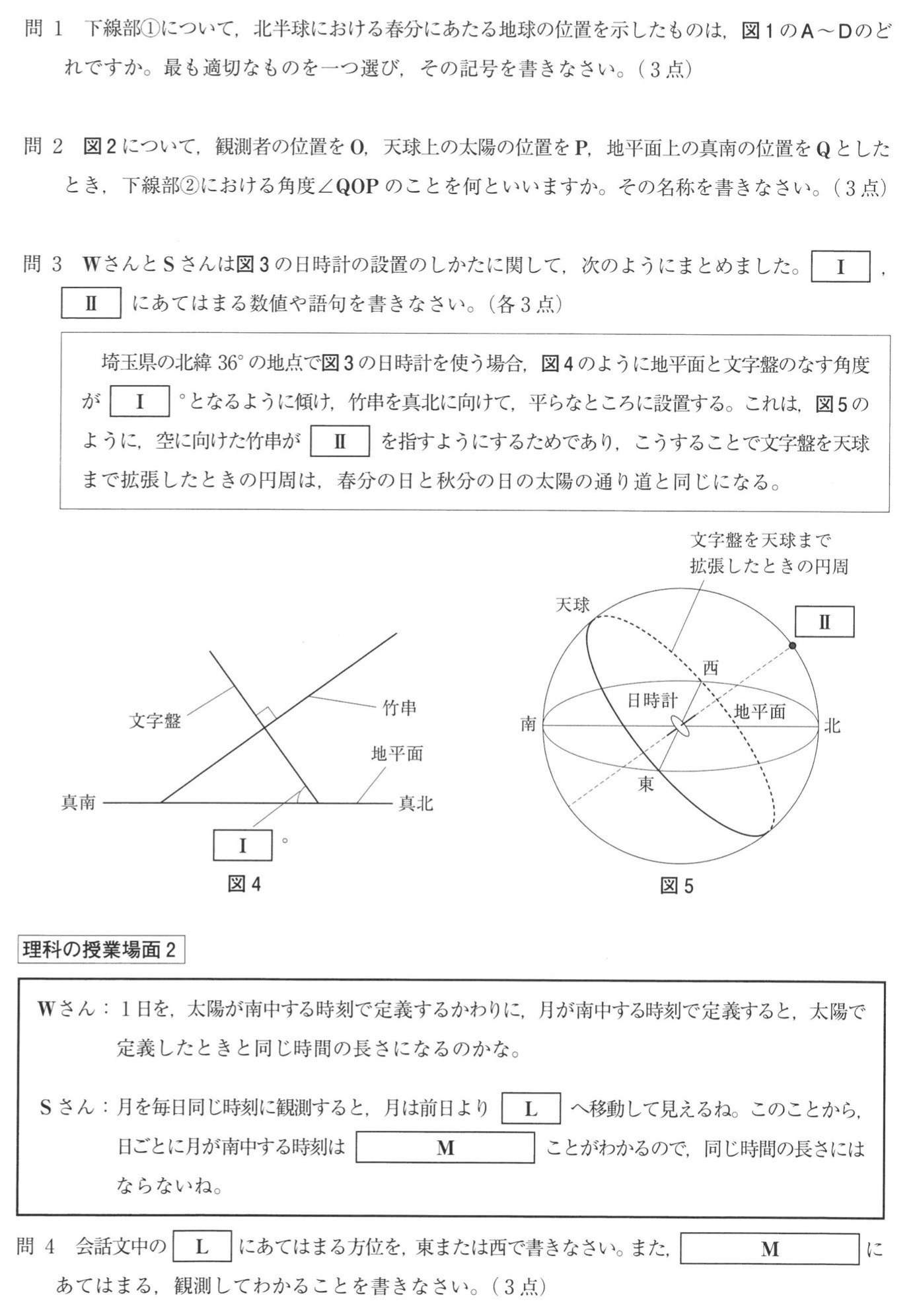
問1
解答:D
解説:
地軸の北極側を太陽に傾けている季節が夏至、太陽と反対方向に傾けている季節が冬至です。
地球は反時計回り(西から東)に太陽の周りを公転しているので、Dが春分です。
問2
解答:南中高度
解説:
単純な知識問題なので、解説略。
問3
解答:Ⅰ・・・54、Ⅱ・・・天の北極(北極星)
解説:
問題文に「文字盤を天球まで拡張したときの円周は、春分の日と秋分の日の太陽の通り道と同じになる」と書かれているので、図2は春分の日と秋分の日の天球上の太陽の通り道で、空欄Ⅰは太陽の南中高度を表します。
春分の日と秋分の日の太陽の南中高度は「90°-緯度」であるので、北緯36°での太陽の南中高度は54°です。
図5より、竹串は天の北極を指しています。
問4
解答:L・・・東、M・・・(例)遅くなっていく
解説:
地球上で月を観測すると、月の満ち欠けの周期が約30日であることから、毎日同じ時刻に月を観察すると、1日あたり約12°(360°÷12°/日)動いて見えます。
月は地球を中心に西から東へ公転していることから、毎日同じ時刻に月を観察すると、1日あたり約12°(360°÷12°/日)、西から東へ動いて見えます。
これより、月が南中してから翌日また南中するには、地球が約12°余計に自転する必要があり、南中時刻は1日あたり約48分ずつ(12°÷15°/時×60分/時)遅くなっていきます。
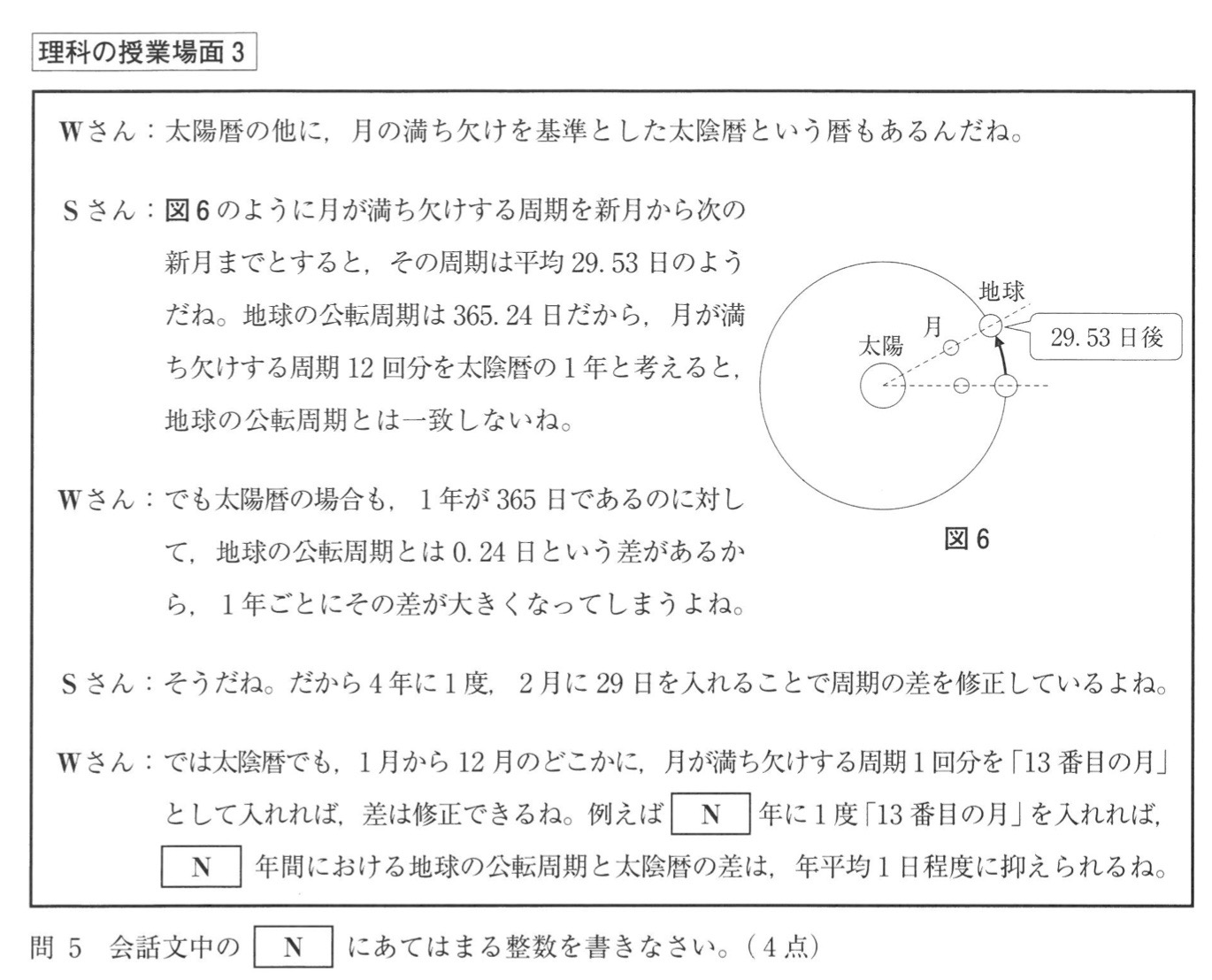
問5 ★難
解答:3
解説:
地球の公転周期=365.24日/年
月が満ち欠けする周期1回分=29.53日/月
太陰暦の1年=29.53日/月×12月/年=354.36日/年
→地球の公転周期と約11日/年=約33日/3年のずれがある。
月の満ち欠けの周期12回分(太陰暦の1年)とのずれは3年で約33日生じるので、3年に1度「13番目の月」として月が満ち欠けする周期1回分(29.53日/月)を入れれば、ずれは約3日(約33日-29.53日)に抑えられます。この3日間のずれは3年間におけるずれなので、1年当たり1日のずれになります。
スポンサーリンク
大問3 細胞呼吸への流れ
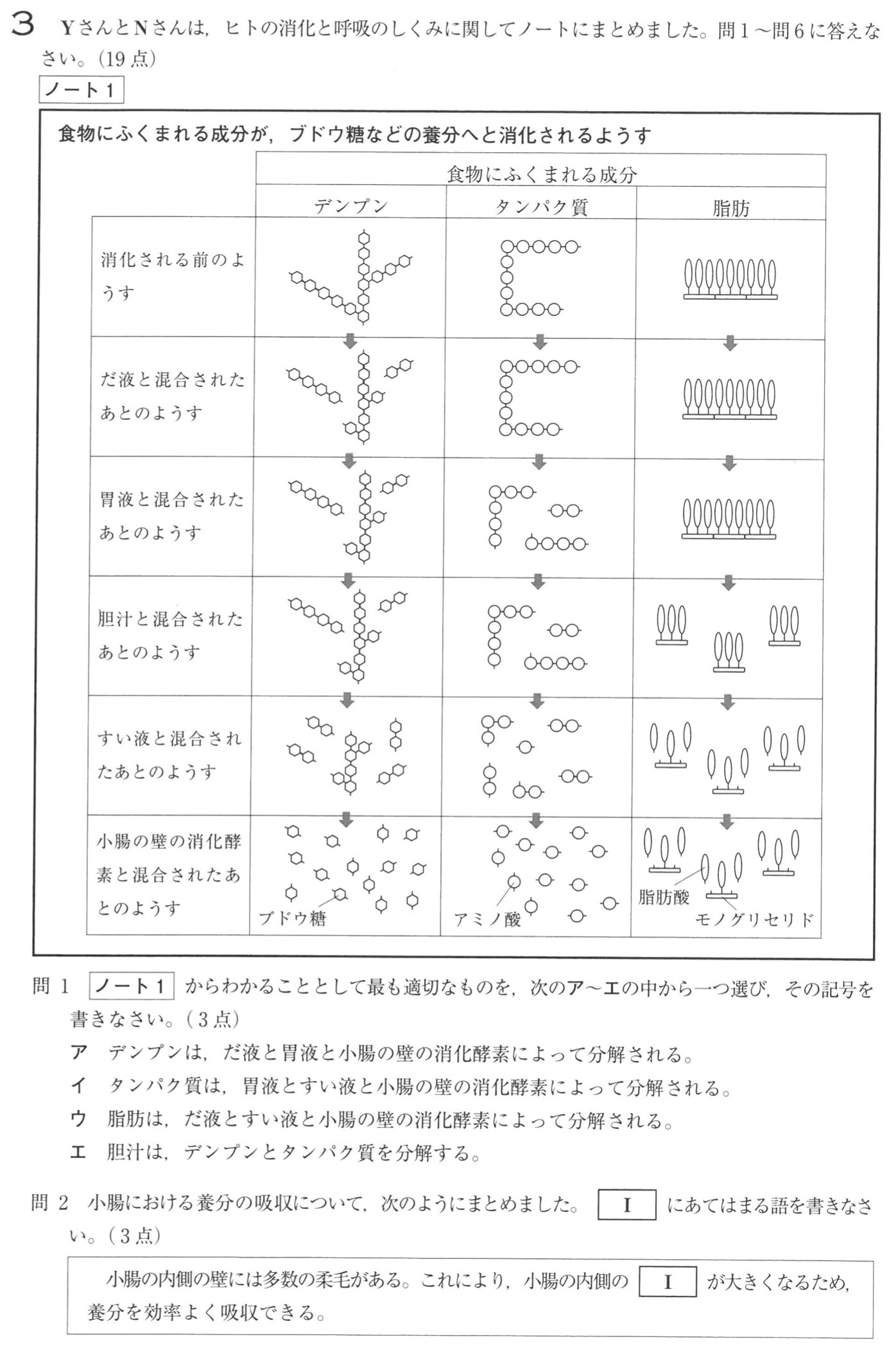

問1
解答:イ
解説:
ア:ノート1より、デンプンは、だ液・すい液・小腸の壁の消化酵素によって分解されることが分かります。
イ:ノート1より、タンパク質は、胃液・すい液・小腸の壁の消化酵素によって分解されることが分かります。よって、正しい。
ウ:ノート1より、脂肪は、胆汁によって細かくされ、すい液の消化酵素によって分解されることが分かります。
エ:ノート1より、胆汁はタンパク質を分解する(細かくする)ことが分かります。
問2
解答:(例)表面積
解説:
小腸の柔毛は、表面積を大きくして養分を効率よく吸収できる利点があります。
問3
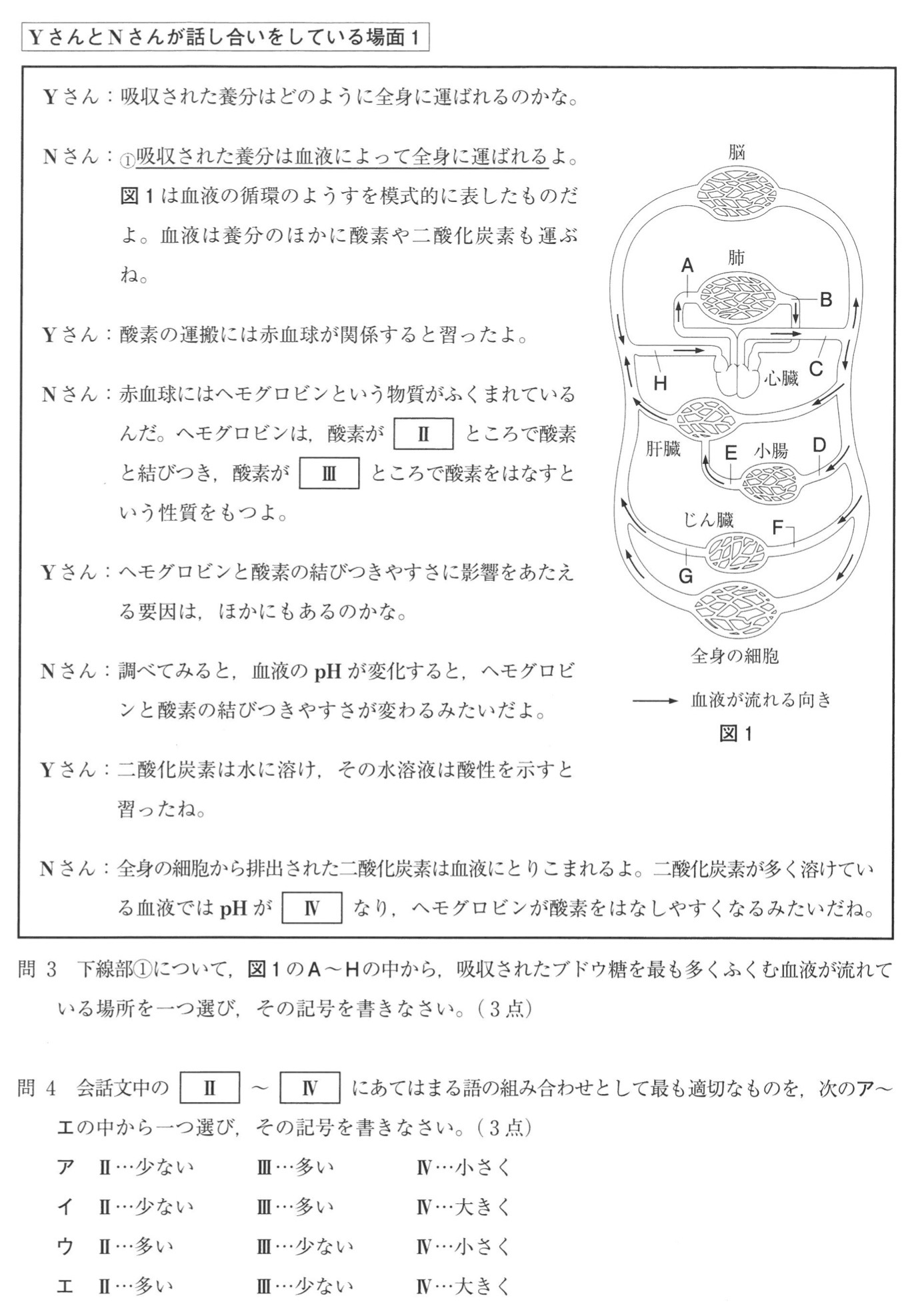
解答:E
解説:
ブドウ糖は小腸の柔毛の毛細血管に吸収された後、門脈(E)を通って肝臓へ行きます。
ブドウ糖は一部が肝臓でグリコーゲンとして蓄えられます。
問4
解答:ウ
解説:
ヘモグロビンは酸素の多いところで酸素と結びつき、酸素が少ないところで酸素を離す性質があります。
二酸化炭素が多く溶けている血液は酸性に傾くので、pHは小さくなります。
問5
解答:ア
解説:
細胞呼吸は「呼吸」なので、養分を燃やして(酸化させて、酸素と結びつけて)生命活動に必要なエネルギーを得ます。
養分は有機物なので、燃えると二酸化炭素と水が発生します。
ブドウ糖は一部が肝臓でグリコーゲンとして蓄えられます。
問6
解答:(例)血液中の養分や酸素は、血しょうに溶けた状態で毛細血管からしみ出て、組織液を通じて全身の細胞に届けられる。
解説:
血液成分である血しょう(液体)が毛細血管からしみ出て、細胞間を満たしているものを組織液といいます。
血しょうには、酸素・養分などが溶けており、これらが組織液を通じて全身の細胞に送り届けられます。
細胞呼吸で生じた二酸化炭素・水・アンモニアは、組織液を通じて毛細血管に送られ、排出されます。
大問4 アンモニア・二酸化炭素・酸素の性質の比較 ★問2(2)がやや難
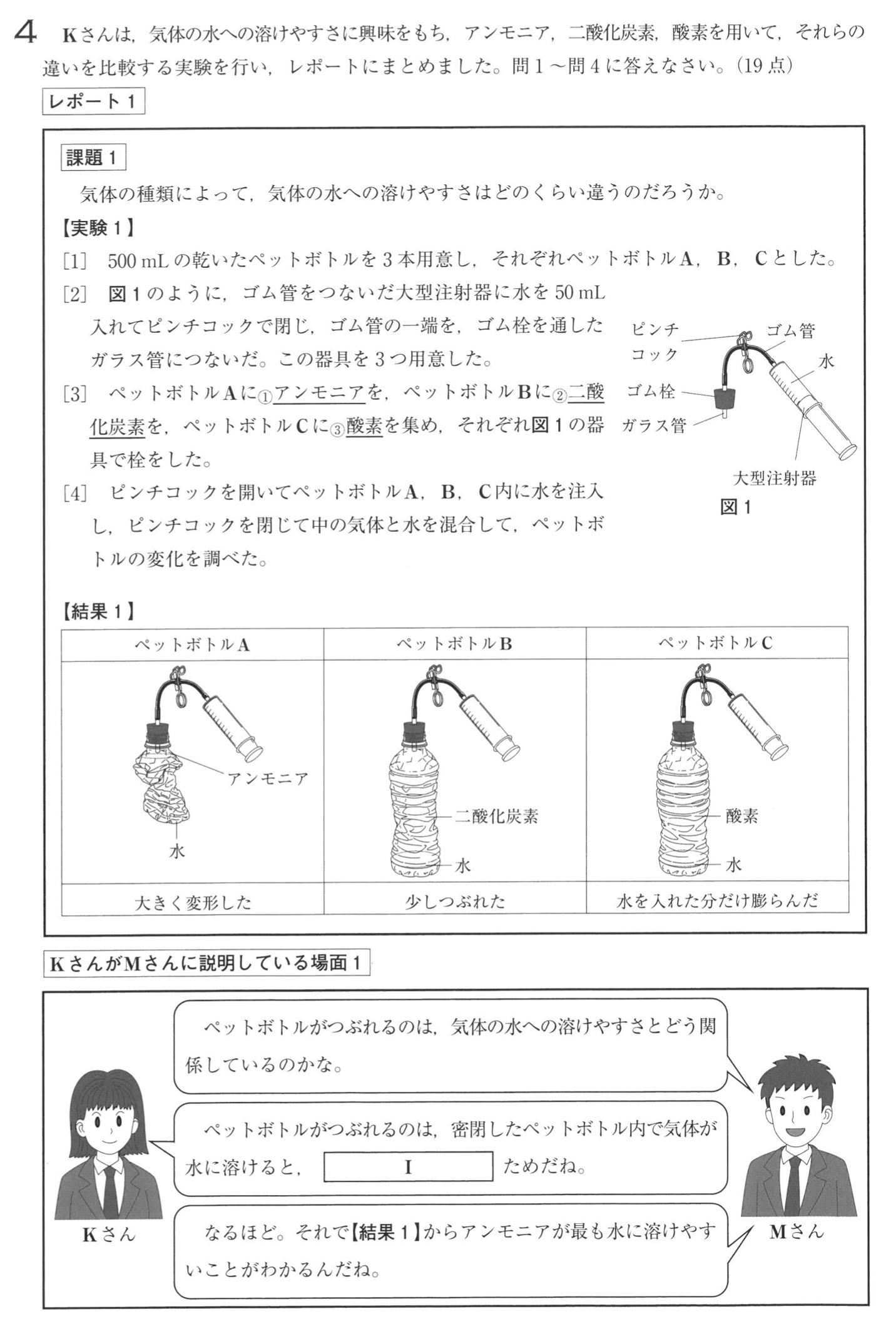

問1
解答:ウ
解説:
乾いたペットボトルにアンモニアが満たされていることを確認するには、選択肢ウのような方法を取ります。
他に、塩酸をつけたガラス棒をペットボトルの口に近づける方法もあります。塩化アンモニウムの白煙が生じたら、乾いたペットボトルにアンモニアが満たされていることが確認できます。
問2(1)
解答:二酸化炭素・・・イ、酸素・・・エ
解説:
ア:水素が発生します。
イ:二酸化炭素が発生します。
ウ:硫化水素が発生します。
エ:酸素が発生します。
問2(2) ★やや難
解答:(例)乾いたペットボトルを使って集めたアンモニアと条件がそろわなくなる
解説:
酸素と二酸化炭素は水上置換法で捕集できます。
しかし、アンモニアは水に非常に溶けやすい(20℃の水1cm3に702cm3溶ける)ので、水上置換法は使えません。
すると実験1は酸素と二酸化炭素は水を満たしたペットボトル、アンモニアは乾いたペットボトルでの実験となり、条件が合わなくなります。
問3
解答:(例)気体として存在している粒子の数が減少することで、大気圧よりペットボトル内の気体の圧力が小さくなる
解説:
問題の条件を満たすように、簡潔に書きます。
気体の粒子の数→減る
大気圧→ペットボトル内の気圧が大気圧より小さくなる
これより、密閉したペットボトル内で気体が水に溶けると、「気体の粒子の数が減少し、ペットボトル内の気圧が大気圧より小さくなる」ため、ペットボトルがつぶれます。
問4
解答:イ
解説:
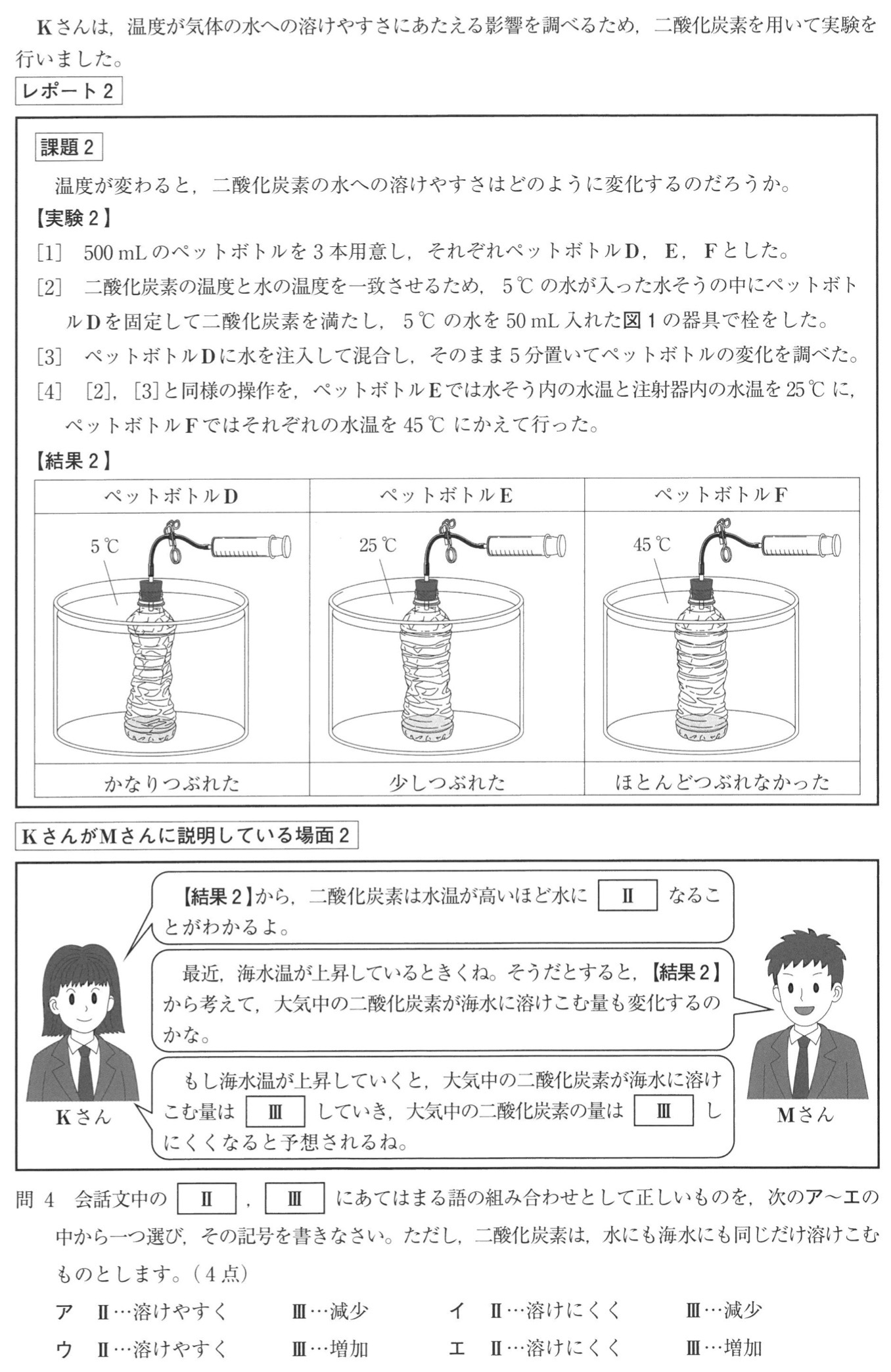
結果2より、二酸化炭素は水温が高いほど水に溶けにくくなることが分かります。
この結果より、もし海水温が上昇していくと、大気中の二酸化炭素が海水に溶けこむ量は減少していき、大気中の二酸化炭素の量が減少しにくくなると予想されます。
大問5 フックの法則と3力のつり合い ★問4が難
問1
解答:
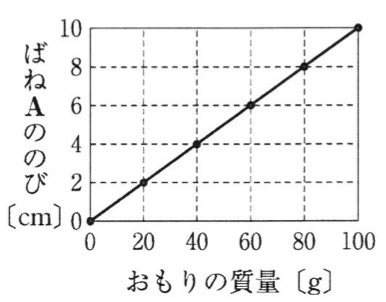
解説:
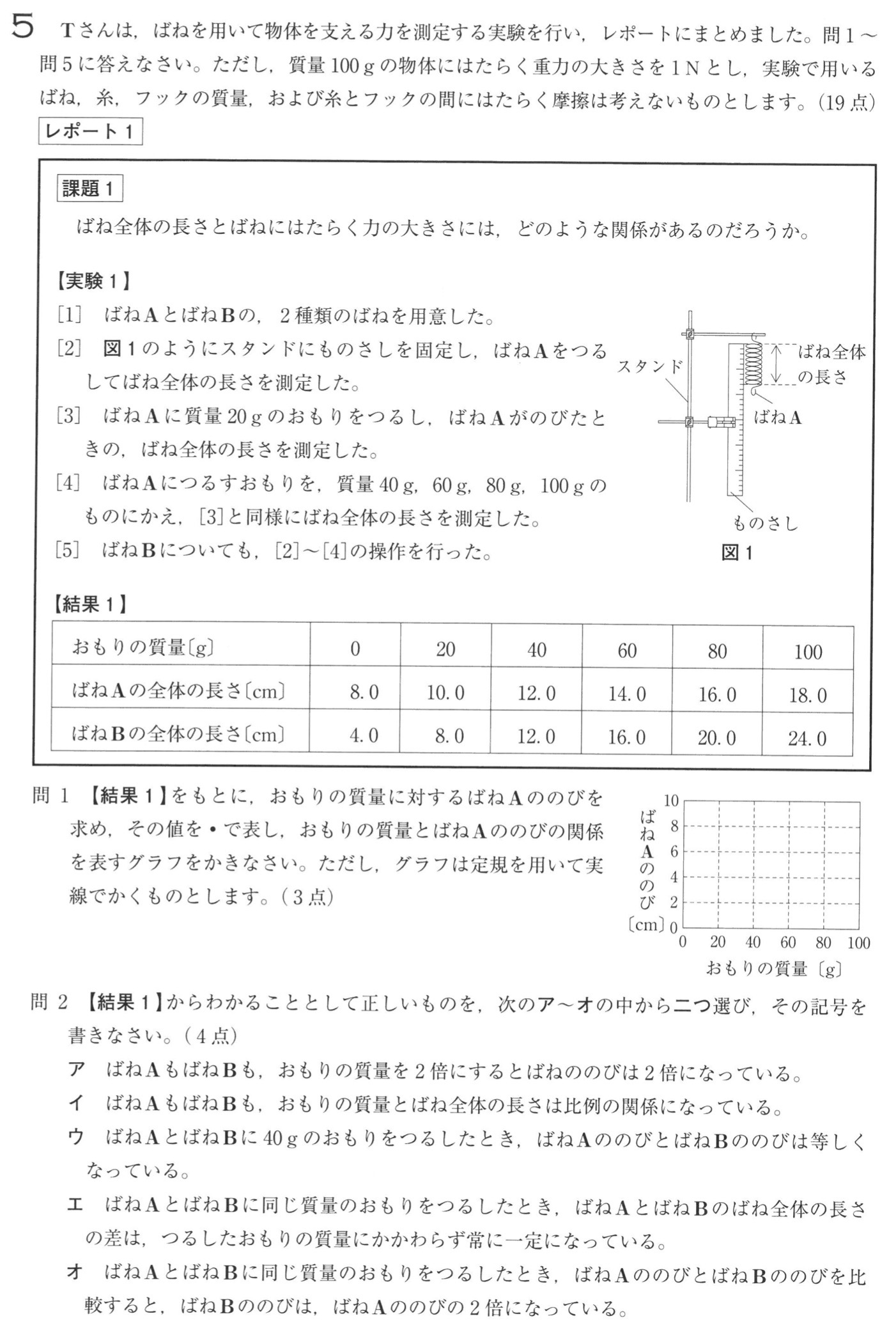
結果1より、おもりの質量が20g増えると、ばねAののびは2cmずつ増加するので、原点を通る傾き2/20の直線を書きます。
問2
解答:アとオ
解説:
ア:おもりの質量を20gから40gに増やすと、ばねAの伸びは2cmから4cm、ばねBののびは4cmから8cmになっているので、正しい。
イ:おもりの質量とばねののびが比例関係になっています。これをフックの法則といいます。
ウ:おもりの質量が40gのとき、ばねAののびは4cmに対して、ばねBののびは8cmとばねAののびの2倍になっています。
エ:おもりの質量が40gのとき、ばねAとBの全体の長さの差は0cmであるのに対して、おもりの質量が60gのとき、ばねAとBの全体の長さの差は2cmと、おもりの質量を増やすと全体の長さの差が変化しています。
オ:おもりの質量が40gのとき、ばねAののびは4cmに対して、ばねBののびは8cmとばねAののびの2倍になっています。よって、正しい。
問3
解答:
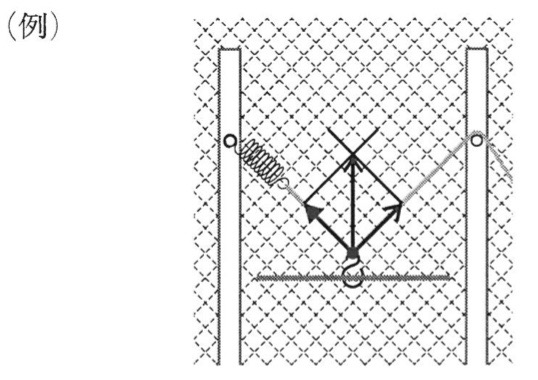
解説:
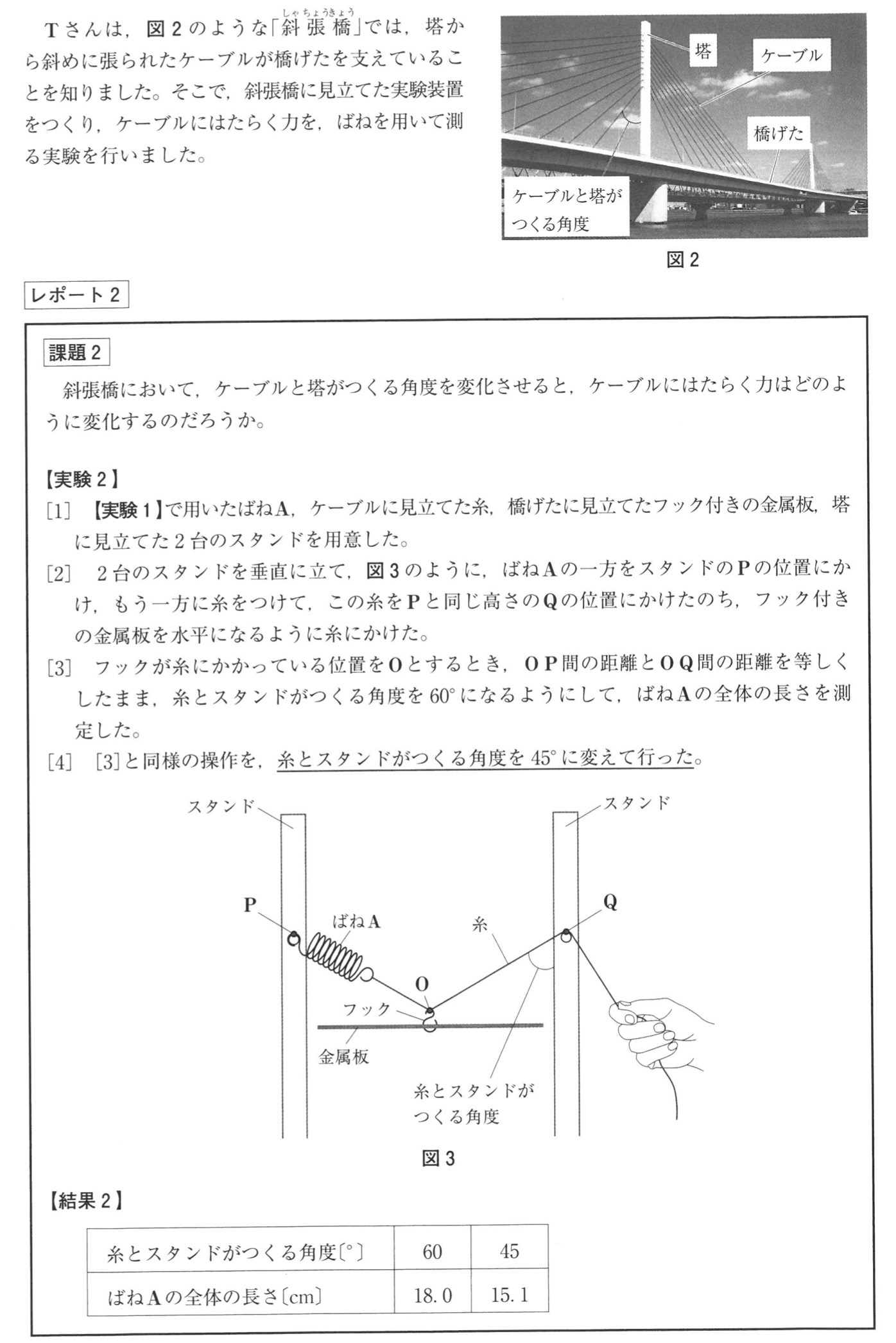
実験2[2]より、OP=OQだから、∠OPQ=∠OQPなので、糸とスタンドがつくる角度は、P点とQ点で等しいです。
点Oにスタンドに平行な線を書くと、錯角が等しいので、OPとOQのばねの開き方が等しいです。
よって、力Ⅰと力Ⅱの大きさは等しいので、力Ⅱは作用点である点Oから点Qへ向けて、力Ⅰと同じ長さになります。
力Ⅲは力Ⅰと力Ⅱを用いて平行四辺形を書いて求められます。
問4 ★難
解答:エ
解説:
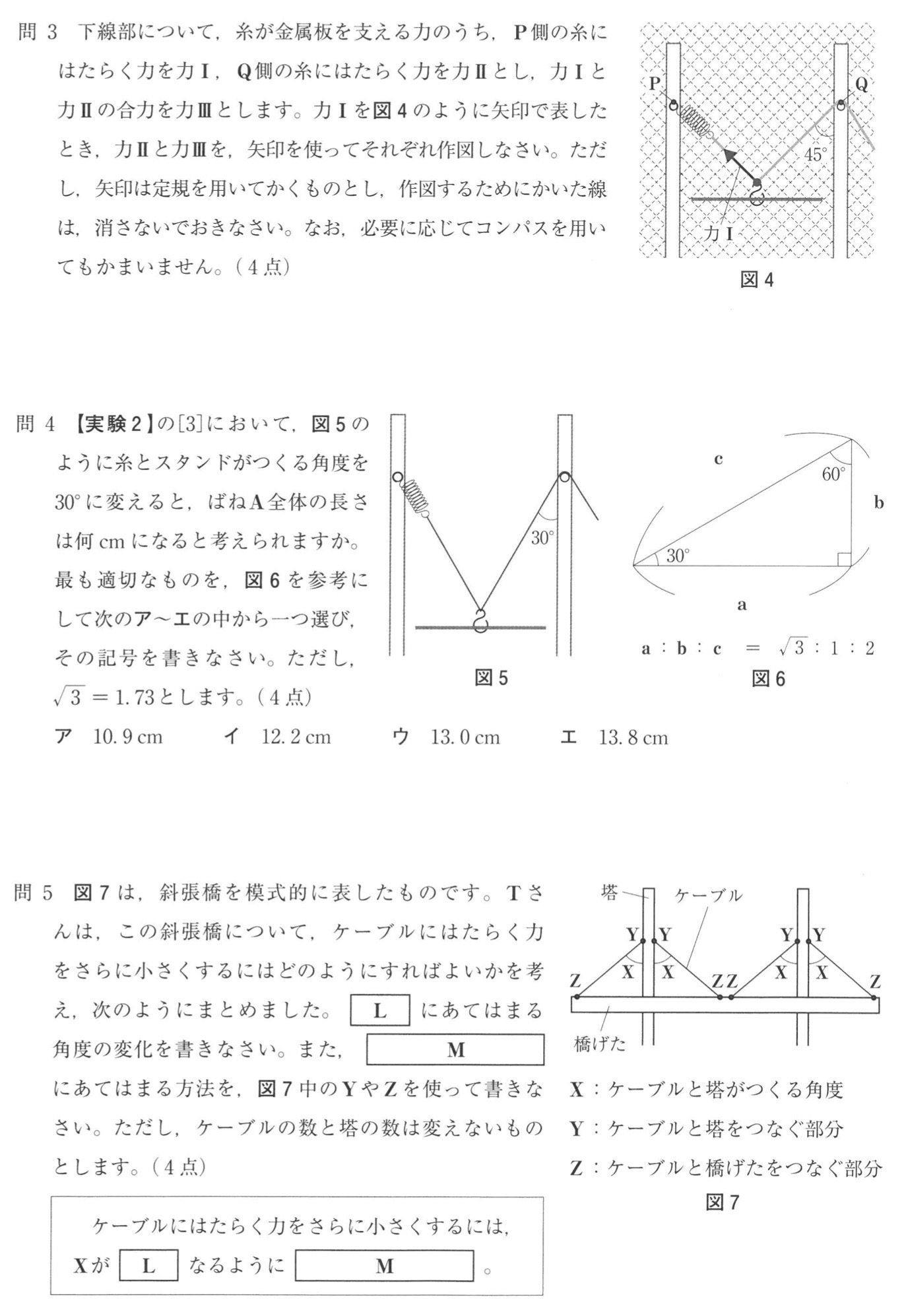
結果2より、糸とスタンドがつくる角度が60°のとき、正三角形ができるので、金属板の重さとばねAと糸にかかる力大きさが等しくなります。
このとき、ばねAの全体の長さが18.0cmなので、10.0cm伸びています。
結果1より、おもり0.2Nにつき、ばねAが2cmのびるので、10.0cmは1.0Nに相当するから、金属板の重さは1.0Nです。
図5において、ばねAと糸が金属板を引く力の合力の大きさが1.0Nで、それは図6の直角三角形の辺aの2倍と見ることができます。
ばねAに加わる力の大きさは、図6の直角三角形の辺cと見ることができるので、3辺比より、
ばねAに加わる力の大きさ=(1.0N/2)×2/√3≒1/1.73N
結果1より、ばねAののび=1/1.73N×(2cm/0.2N)=2×5/1.73=10/1.73=5.780・・・≒5.8cm
結果1より、ばねAの自然長は8cmなので、ばねAの全体の長さ=8cm+5.8cm=13.8cm
問5
解答:L・・・小さく、M・・・(例)Yを高くする
解説:
結果2と問4の考察より、開き方が小さくなると、ばねAにかかる力の大きさが小さくなります。
だから、図7のケーブルにはたらく力の大きさを小さくするには、Xを小さくすればよいです。
Xを小さくするには、ケーブルと橋をつなぐ部分であるYを高くしたり、ケーブルと橋げたをつなぐ部分であるZと橋との距離を短くする、などの方法をとるとよいです。


