こんにちは、個別指導塾まさです。
今回は、中1理科3学期定期テスト（学年末テスト）過去問の解説第3弾です。
実際に定期テストで出題された問題の中で、とくに差が付く問題を厳選して解説します。
オンライン個別指導塾と家庭教師をやっています。北大院卒、指導経験20年以上。当塾は中上位高校志望の子が多いですが、勉強が苦手な子も多数在籍しています。今の学力は不問ですので、気軽にお申し込みください。授業料は1回70分 3,000円〜です。
＞＞教師紹介・料金・授業内容
＞＞体験授業かんたんお申し込み
＞＞お問い合わせ
第1問
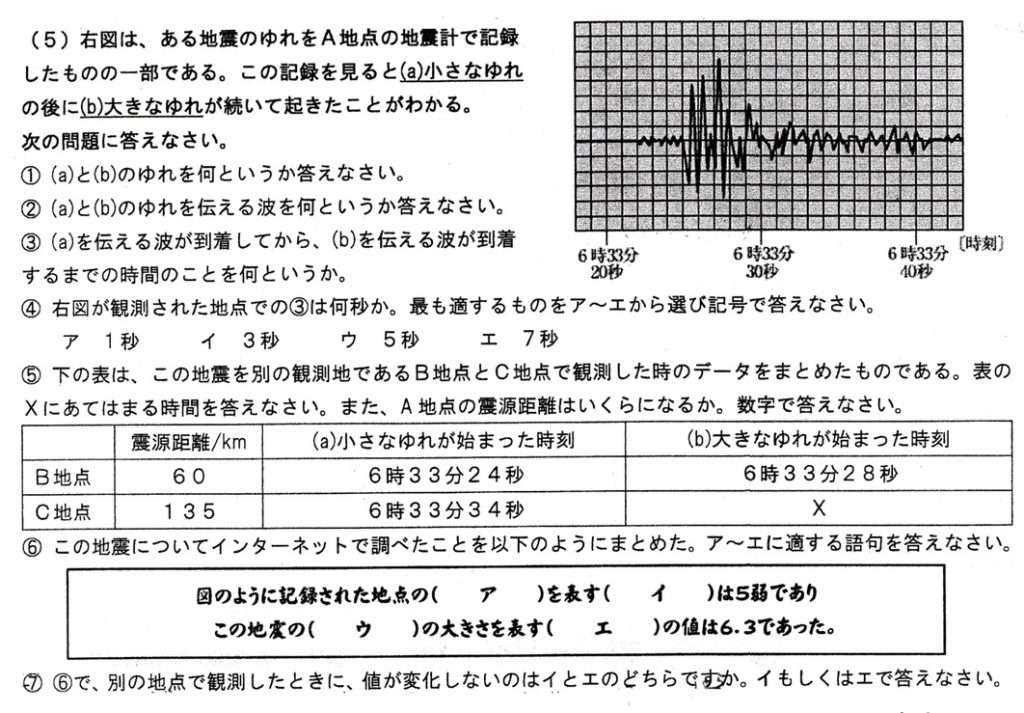
（1）
答：（a）初期微動、（b）主要動
（2）
答：（a）P波、（b）S波
（3）
答：初期微動継続時間
（4）
1マスが1秒に相当し、初期微動継続時間は3マスより、3秒（イ）となります。
（5）
・X
B地点の初期微動継続時間が4秒、C地点の震源距離はB地点の135/60倍より、
C地点の初期微動継続時間＝4s×135/60=135/15=9s
ゆえに、C地点にS波が届いた時刻は、6:33.34＋9s＝6:33.43
・A地点の震源距離
B地点の初期微動継続時間が4秒、A地点の初期微動継続時間はB地点の3/4倍、B地点の震源距離は60kmより、
A地点の震源距離＝60km×3/4=15×3=45km
（6）
ア、イ
「5弱」とあるので、揺れの大きさを示す震度です。
ウ、エ
6.3と小数まで表記されているので、地震の規模を示すマグニチュードです。
（7）
震度は揺れの大きさなので場所により変化しますが、マグニチュード（エ）は地震のエネルギーなので場所によって変化しません。
第2問（やや難）
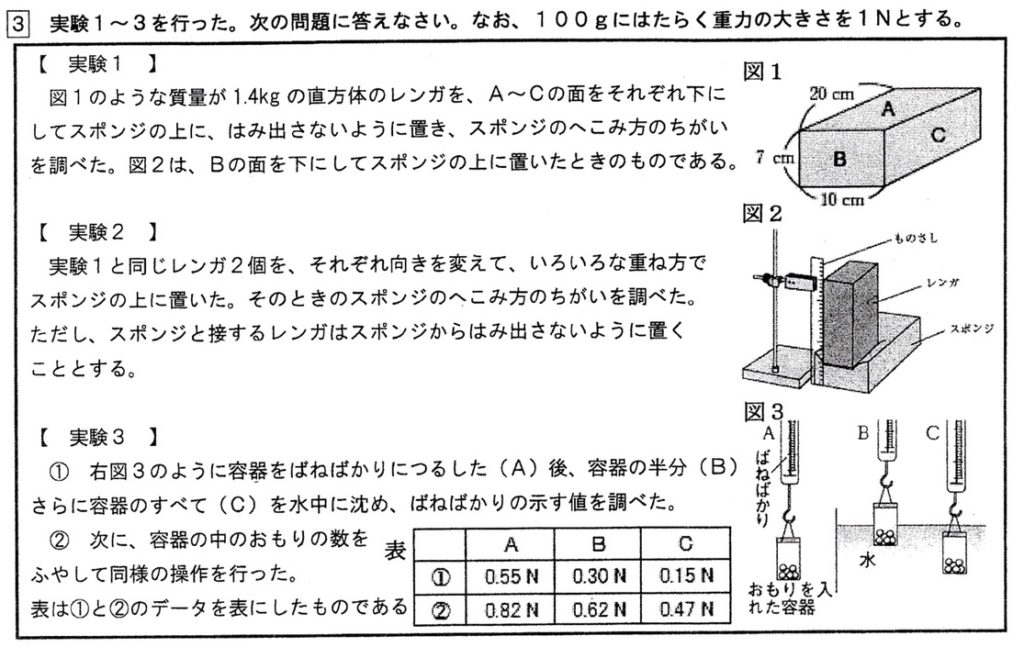
（1）
力は作用点と矢印の長さで表され、面に依存しません。
ゆえに、A面とC面で、スポンジを押す力の大きさは変わりません。
1.4kg=1400gは仮定より14Nに相当するので、レンガにはたらく重力の大きさ＝レンガがスポンジを押す力の大きさは14Nです。
（2）
圧力の単位（N/m2）に留意して、
A面の圧力＝14N÷(20/100m×10/100m)＝14×100×100÷(20×10)=14×5×10＝70×100=700N/m2=700Pa
圧力の比は面積比の逆比となり、C面はA面の7/10倍なので、C面の圧力はA面の10/7倍≒1.4倍とA面より大きくなります。
（3）
圧力が最も大きくなる面を探します。
圧力の単位（N/m2）に留意して、圧力は面積に反比例するので、面積が最も小さいB面が圧力が最も大きくなります。
（4）＜やや難＞
圧力の単位（N/m2）に留意して、面積をxとおいて計算すると、
14N×2/x=14N÷(7cm×10cm)
x=2×7×10cm2=20×7cm2
これより、C面となります。
C面の圧力は、14N×2÷(20×7cm2)=14×2×100×100÷(20×7)=2×10×100=2000N/m2=2000Pa
（5）＜難＞
・BとC
「BとCの結果を比較することで」とあるので、素直に従って比較すると、BからCで①と②でばねばかりの示す値はともに0.15N減少しており、この値が浮力に相当します。
BとCで変化しているのは、水に沈んだ容器の体積です。
ゆえに、「浮力の大きさは容器が押しのけた水の体積に依存する」といえます。
・①と②
「BとC」の比較から、①と②で「浮力の大きさは物体の質量に依存しない」と言えます。
（6）
②の容器において、Cは完全に沈んでおり、浮力の大きさは0.35Nです。
ゆえに、Dにおける浮力の大きさも0.35Nなので、ばねばかりの示す値は0.47Nのままです。
（7）
「浮かぶ」というのが容器が水中にどのくらい沈んだときか、条件が与えられていません。
また、表において、AからCのときのばねばかりの示す値の減少値が、①が0.40N、②が0.35Nですが、同じ容器で完全に沈めたのですから、浮力の大きさも同じくなるはずです。
しかし、実際は浮力の大きさが変化しており、一意に決定することができません。
残念ながら、この問題は解くことができません。
スポンサーリンク
第3問
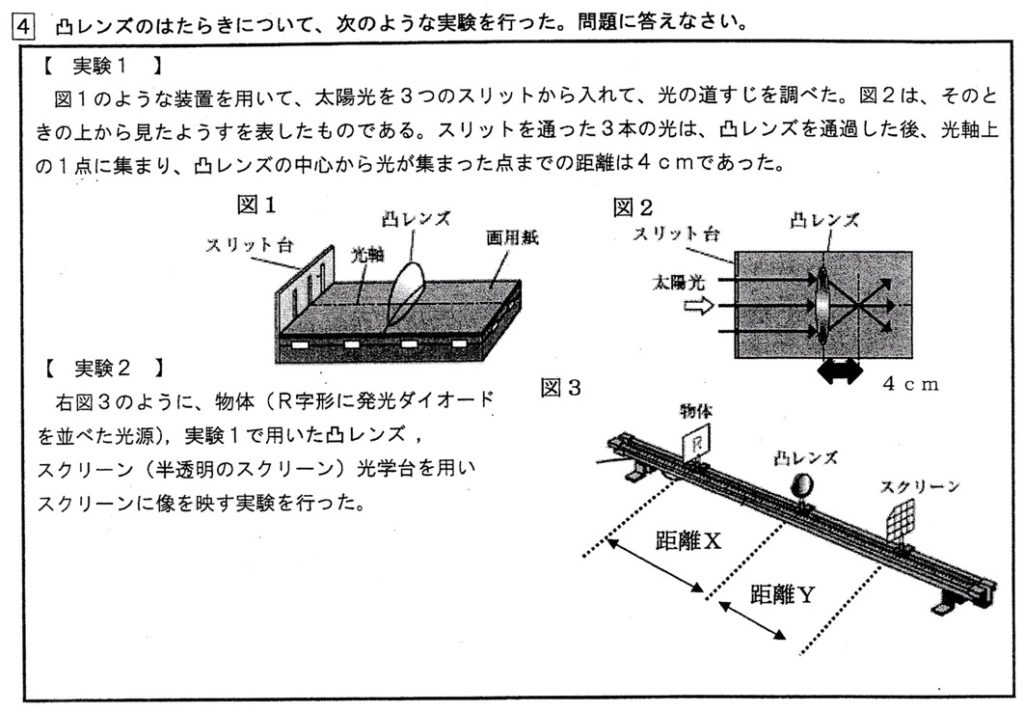
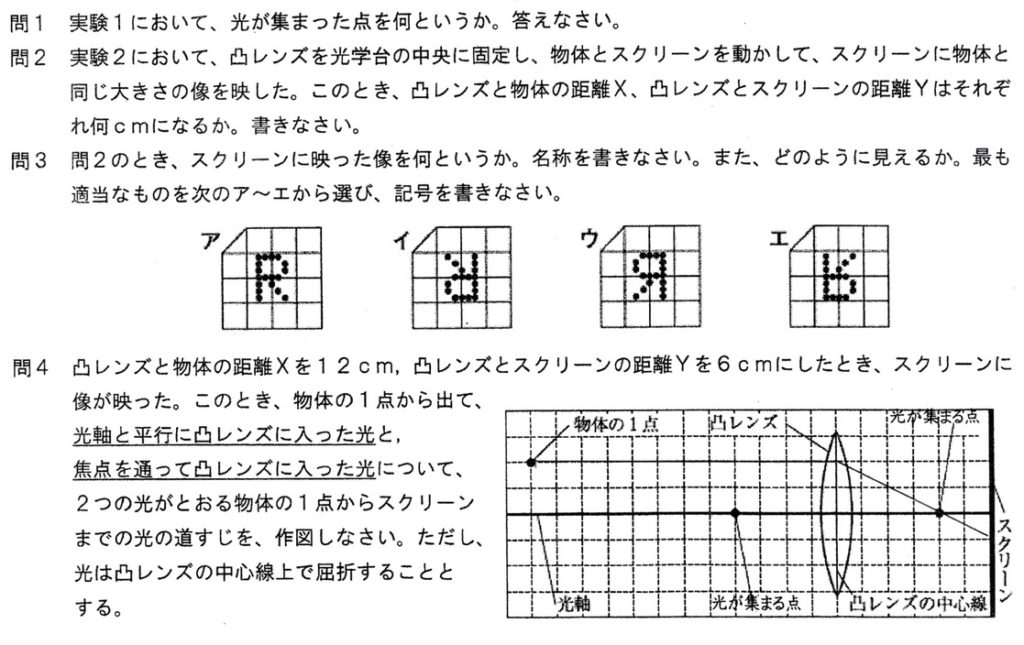
（1）
答：焦点
（2）
実験1より、この凸レンズの焦点距離は4cmです。
スクリーンに物体と同じ大きさの倒立実像ができたとき、物体は凸レンズの焦点距離の2倍の位置にいるので、Xは8cmです。
このとき、物体と凸レンズとの距離と、凸レンズと倒立実像との距離が（三角形の合同より）等しくなるので、Yも8cmです。
（3）
光が集まってできる像なので、倒立実像です。
倒立実像は、凸レンズ側からスクリーンに映った像を見ると上下が逆に、スクリーン側から像を見ると上下左右が逆に見えます。
（4）
略
（5）
物体はちょうど凸レンズの焦点の位置にあるので、像はできません。
物体が凸レンズの焦点の内側にあるとき、凸レンズを通して実物より大きい正立虚像が見えます（イ）
（6）
スクリーンに物体が映る場合なので、倒立実像を考えます。
物体を凸レンズに近づけていくと、像は遠ざかりながら大きくなっていきます。
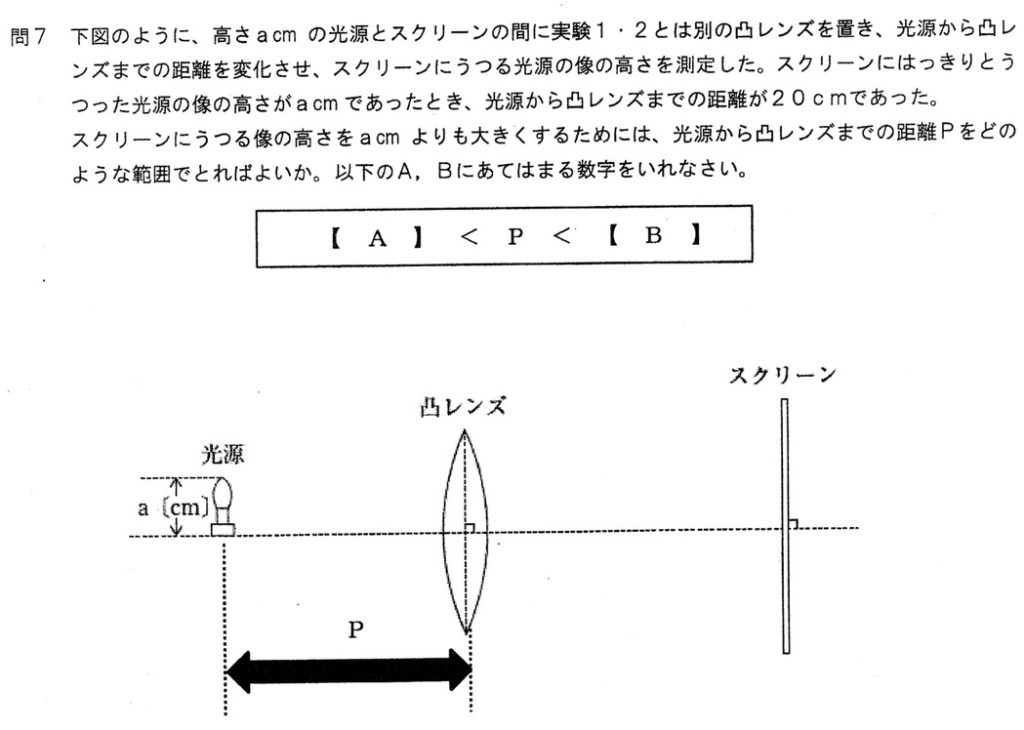
（7）＜やや難＞
光源とスクリーンの大きさ（高さ）がa cmと同じなので、この凸レンズの焦点距離は10cmです。
像の大きさは、焦点距離（10cm）より大きく焦点距離の2倍（20cm）より小さい範囲に像がいるとき、実物より大きくなります。
