こんにちは、個別指導塾まさです。
＞＞【最新版】大阪府公立・私立高校入試おすすめ過去問題集（高校別一覧）
＞＞【最新版】兵庫県の公立・私立高校入試おすすめ過去問題集（高校別一覧）
＞＞【最新版】京都府の公立・国立・私立高校入試おすすめ過去問題集（高校別一覧）
＞＞【最新版】奈良県の公立・私立高校入試おすすめ過去問題集（高校別一覧）
今回は、2022年に行われた、大阪府公立高校入試「理科」の問題・解答・詳しい解説を公開致します。
※大問3の天体の問題が難しいですが、他は標準レベルの問題セットです。基礎力チェックとしておすすめします。
オンライン個別指導塾と家庭教師をやっています。北大院卒、指導経験20年以上。当塾は中上位高校志望の子が多いですが、勉強が苦手な子も多数在籍しています。今の学力は不問ですので、気軽にお申し込みください。授業料は1回70分 3,000円〜です。
＞＞教師紹介・料金・授業内容
＞＞体験授業かんたんお申し込み
＞＞お問い合わせ
大問1 食物連鎖
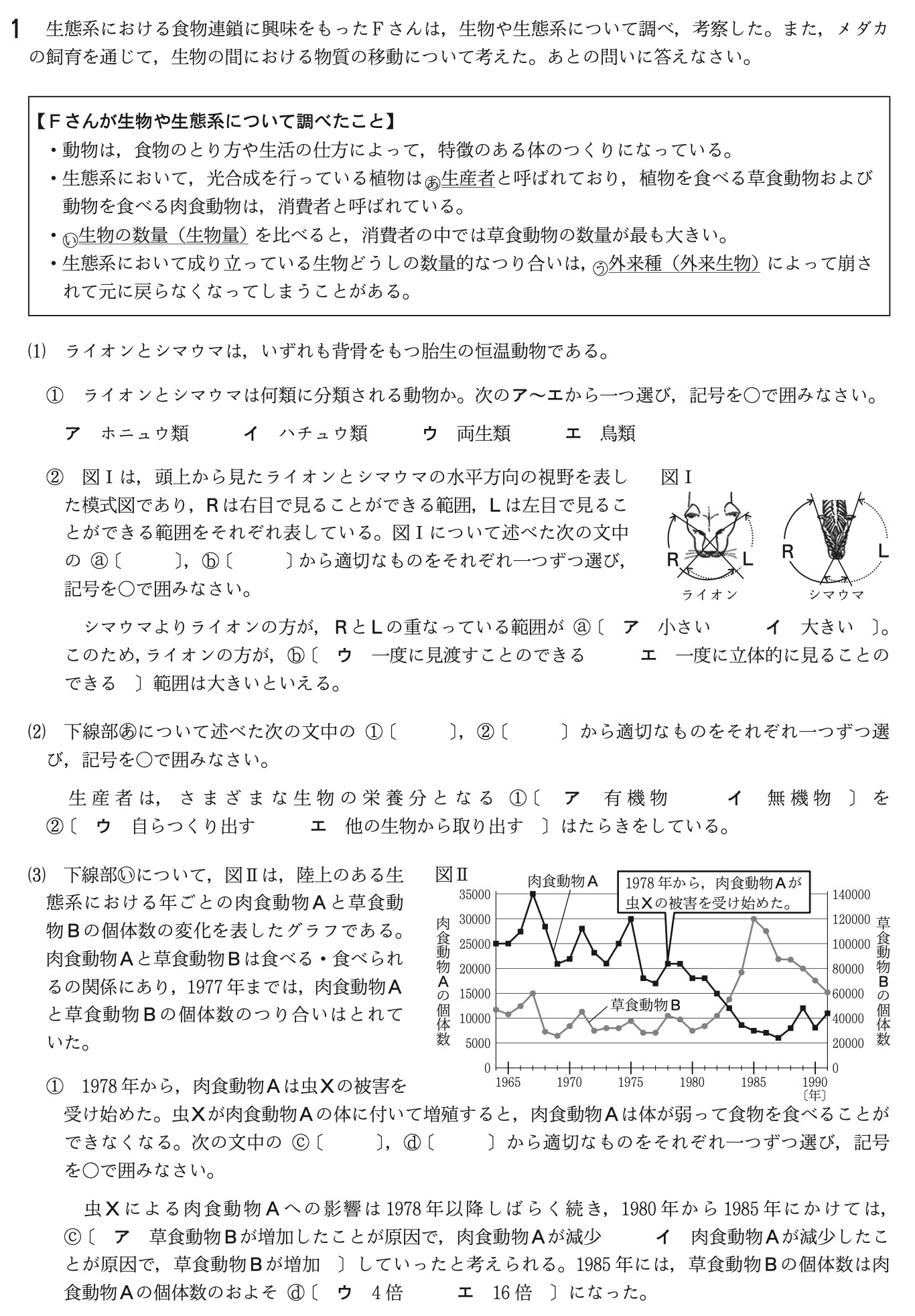
（1）①
解答：ア
解説：
問題文に「ライオンとシマウマは、いずれも背骨をもつ胎生の恒温動物である。」とあるので、ライオンとシマウマは、ホニュウ類です。
（1）②a
解答：イ
（1）②b
解答：エ
解説：
図1のRとLの範囲は視野、RとLに挟まれた部分は立体的に見える範囲です。
問題文に「図1について述べた次の文」とあるので、図1をよく見ながら解いていきます。
シマウマよりライオンの方が、RとLの重なっている範囲が大きいです。
このため、ライオンの方が立体的に見える範囲が大きく、獲物との距離感がつかみやすくなります。
（2）①
解答：ア
（2）②
解答：ウ
解説：
ピラミッドの底辺である生産者は、必ず植物になります。
植物は光合成により、有機物を自ら作り出すはたらきをしています。
（3）①c
解答：イ
解説：
図2を見ると、1980年から1985年にかけては、肉食動物は減少し、草食動物は増加しています。
これは、食べる立場の肉食動物の個体数が減少したため、食べられる立場の草食動物が増加したからです。
（3）①d
解答：エ
解説：
図2はグラフですので、縦軸と横軸の種類を必ず確認してから、グラフを見るようにしてください。
1985年の草食動物Bの個体数は、グラフ縦軸の右側を見て、およそ120000です。
肉食動物Aの個体数は、グラフ縦軸の左側を見て、およそ7500です。
よって、草食動物Bの個体数は、肉食動物Aの個体数のおよそ、
120000/7500＝1200/75倍で、選択肢より、明らかに4倍ではないので、選択肢エの16倍を選びます。
（3）②
解答：ウ
解説：
1985年から1987年は、肉食動物A・草食動物Bともに個体数が減少しています。
これより、草食動物Bの個体数が減少した原因は、肉食動物Aの個体数が増加したことではないことが分かります（選択肢アとイはダメ）。
選択肢ウとエは、草食動物Bと植物との関係が述べられています。
草食動物は植物を食べる消費者（一次消費者）です。
グラフより、1985年には草食動物Bの個体数がピークを迎えており、個体数が非常に多くなっています。
それが原因で、草食動物Bの食料となる植物が不足したため、草食動物Bの個体数が減少したと考えられます。
（4）
解答：人間
解説：
単純な知識問題なので、解説略。
（5）
解答：エ
解説：
ア：二酸化炭素の性質です。
イ：塩素の性質です。
ウ：中学理科の範囲では、アンモニアの性質です。
エ：正しい。
（6）①
解答：ア
（6）②
解答：分解
解説：
メダカのふんは排出物、つまり有機物なので、分解者が呼吸をして無機物に分解します。
分解者は、菌類（カビやキノコなど）・細菌類（乳酸菌や大腸菌など）・土の中の小動物（トビムシ、ミミズ、ダンゴムシ）に分けられます。
（7）
解答：カ
解説：
オオカナダモは光合成をして酸素（O2）をつくり、メダカはそれを呼吸に利用して、二酸化炭素（CO2）を排出します。
よって、オオカナダモからメダカに炭素（C）は移動していなく、メダカからオオカナダモに炭素（C）移動しています。
オオカナダモとメダカの間のみで考えると、炭素（C）はメダカからオオカナダモに一方的に移動しており、繰り返し移動していません。
スポンサーリンク
大問2 状態変化とエネルギーの移り変わり ★(3)がやや難
（1）①
解答：エ
解説：
水素分子が2つあるので、選択肢エが正解です。
（1）②
解答：純粋な物質
解説：
水の化学式はH2Oで、水素と酸素（ともに単体）を含む化合物です。
単体、化合物ともに純粋な物質で、決まった融点と沸点を持ちます。
（2）
解答：ア
解説：
単純な知識問題なので、解説略。
（3） ★やや難
解答：水の状態変化に利用された熱量
解説：
問題文に「Y先生の助言1をふまえ」「「熱量」の語を用いて書きなさい」とあるので、Y先生の助言1の文章をよく読みます。
Y先生の助言1より、「熱量」と書かれているのは、「水温の上昇に利用された熱量」と「水の状態変化に利用された熱量」です。そして、ここから以下の式が導けます。
・水に加えられる1分あたりの熱量＝水温の上昇に利用された熱量＋水の状態変化に利用された熱量
再び問題文を読むと、水に加えられる1分あたりの熱量はつねに一定です。
しかし、加熱時間に対する水温の上昇の割合が徐々に小さくなっていったことから、「水温の上昇に利用された熱量」が小さくなり、「水の状態変化に利用された熱量」が増加したことが分かります。
（4）
解答：25L
解説：
100℃の水蒸気1Lあたりの質量は0.60gであるので15gでは、
15g÷0.60g/L＝150/6＝25L
（5）
解答：ウ
解説：
沸とうしている水の温度は、純粋な水であるので、100℃です。
継続して熱を加えると、水＋水蒸気の状態から水蒸気の状態に変化していきます。
これより、気体の水の体積が増えるため、鍋のふたはもち上がったと考えられます。
以上の考察をもとに、空欄を埋めていきます。
質量に変化はないので、液体の水の質量と体積が減って、気体の水の質量と体積が増えています。
ただし、液体の水から気体の水に状態変化すると、体積は激増して、鍋のふたを持ち上げます。
（6）d
解答：イ
（6）e
解答：エ
解説：
たとえば、モーターを回すとき、電気エネルギーがモーターの運動エネルギーに変換されますが、一部が熱エネルギーや音エネルギーに変換されるため、電気エネルギーがすべて運動エネルギーに変換されません。
この例をもとに、考察していきます。
エネルギー保存の法則より、変換前のエネルギーの総量と変換後のエネルギーの総量は変わりません。
しかし、変換後の目的のエネルギーの量は、変換前のエネルギーの総量より小さくなります。
（7）
解答：エ
解説：
単純な知識問題なので、解説略。
スポンサーリンク
大問3 天体全般（金星・星・太陽の動き） ★全般的にやや難
※見慣れない題材ですが、教科書レベルの知識に還元できることがカギです。
（1）
解答：日食
解説：
地球-月-太陽の順に並んでいるので、日食が起こります。
（2）
解答：ウ
解説：
内惑星である水星と金星は真夜中に観察できませんが、外惑星である火星は真夜中に観察できます。
問題文に「2021年には水星、金星、火星が月にかくされる現象がそれぞれ2回ずつ、合計6回起こった。」とあるので、
火星のみ真夜中に月にかくされる現象を観測できることがあります。
（3）①
解答：ア
（3）②
解答：エ
解説：
問題文より、2021年11月8日の金星、地球、太陽の位置関係は、図1を見れば分かります。
図1より、金星はよいの明星の位置にあり、夕方西の空に観察できます、
（4）
解答：イ
解説：
問題文より、月は13時44分ごろから14時26分ごろの南南東の空で観察できることから、月は右側が少し光った三日月の形をしています。
（5）
解答：自転
解説：
恒星の日周運動は、地球の自転によって起こります。
恒星は惑星とは異なり、非常に遠くにあるため、届く光は平行光線です。
このため、互いの位置関係を変えずに、地球の周りを回っているように観測できます（見かけの動き）。
（6）
解答：イ
解説：
地球は地軸の北極側を公転面に垂直な線に対して23.4°傾けているため、公転により同一地点の南中高度が変化します。
同一地点の南中高度が最も高くなるのは、地軸の北極側を太陽の方に傾けている夏至です。
（7）
解答：11月末ごろ
解説：
問題文より、アンタレスは7月29日の20時ごろに真南の空に観測され、1か月経つにつれて2時間早く南中してくので、4か月後の11月29日（11月末ごろ）では12時（正午）に南中します。
（8）①
解答：イ
解説：
2022年3月19日は、明け方西の空に月が観測できることから、満月です。
そこから日にちごとに、月は右側から欠けていきます。
（8）②
解答：ウ
解説：
2022年3月19日は、明け方南の空に月が観測できることから、左側半分が光った下弦の月です。
天体上で考えると、明け方南の空では、左側が東、右側が西の方角になります。
（9）
解答：西から東へ移動
解説：
月の年周運動を考えると、太陽と同様に、月は星座の間を西から東へ移動して見えます。
しかし、月の公転周期は27.3日と、地球の公転周期1年よりはるかに短いため、星座の間を移動する速度が、月は太陽よりも大きいです。
太陽は月の400倍離れています。
このため、太陽は月の東側から月の後ろにかくれ始め、月の西側から出てくると考えられます。
大問4 フックの法則と浮力 ★（6）③と（7）がやや難
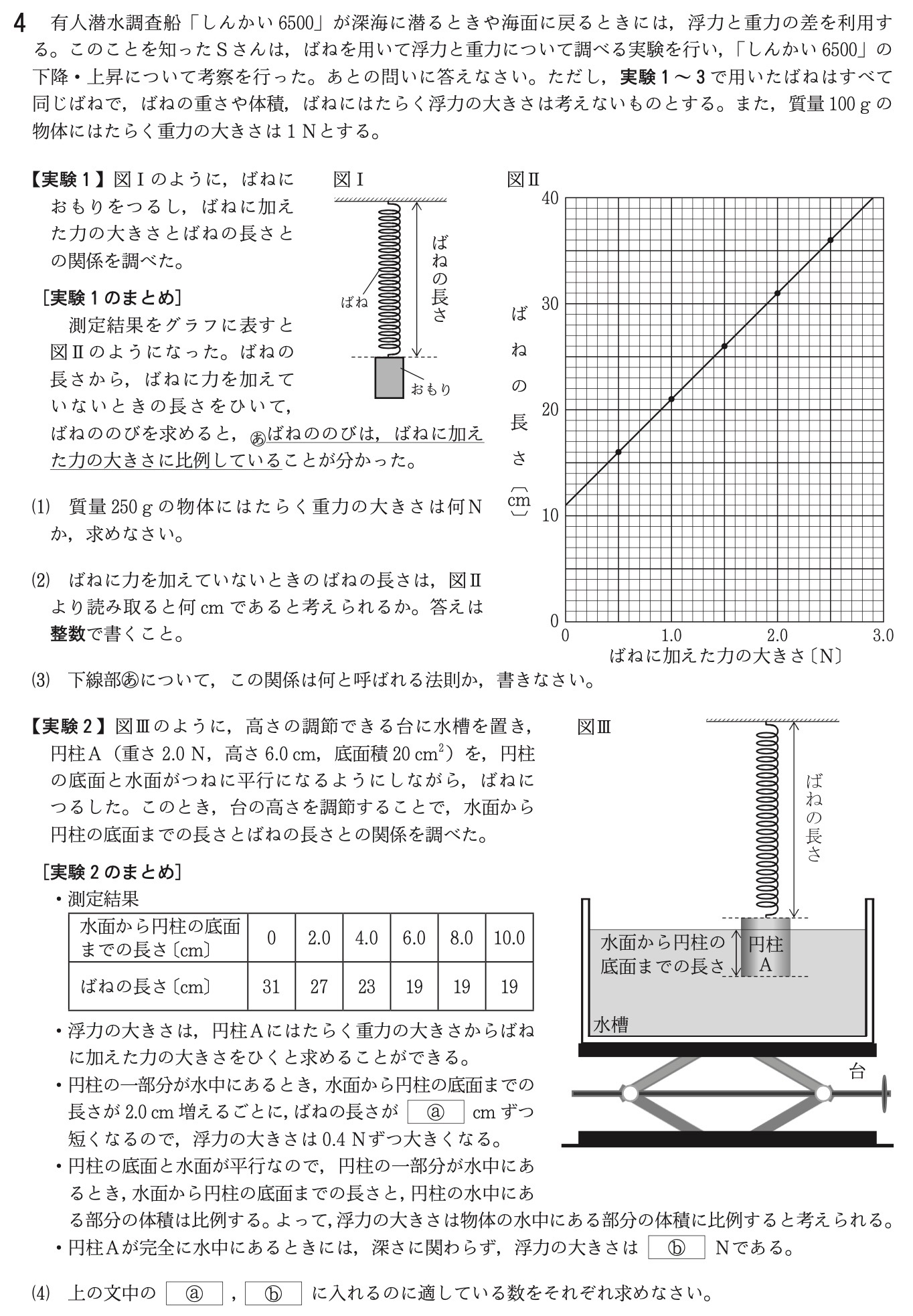
（1）
解答：2.5N
解説：
(1N/100g)×250g＝2.5N
（2）
解答：11cm
解説：
図2より、ばねの自然長は0Nのときのばねの長さ11cmです。
ばねに加えた力の大きさが1.0Nのとき、ばねの長さは21cmです。
よって、このばねは、1.0Nの力を加えると10cmのびます。
（3）
解答：フックの法則
解説：
単純な知識問題なので、解説略。
（4）a
解答：4cm
解説：
「・測定結果」より、水面から円柱の底面までの長さが2.0cm増えるごとに、ばねの長さは4cmずつ短くなっています。
このばねの長さが浮力の大きさに相当します。
このばねは、1.0Nの力を加えると10cmのびることから、水面から円柱の底面までの長さが2.0cm増えるごとに、浮力の大きさは、4cm÷(10cm/1.0N)＝0.4N増えていきます。
（4）b
解答：1.2N
解説：
ばねの長さが31cmから19cmと12cm縮んでいることから、浮力の大きさは、12cm÷(10cm/1.0N)＝1.2Nです。
（5）①
解答：ア
（5）②
解答：ウ
解説：
問題文より、「浮力の大きさ＜重力の大きさ」なので、しんかい6500は等加速度運動をしながら沈みます。
しかし実際には、しんかい6500にはたらく上下方向の力の大きさがつり合うため、等速直線運動をして沈みます。
よって、「浮力の大きさ＋動きをさまたげる力＝重力の大きさ」であることから、この力は浮力の向きと同じ上向きの力であると考えられます。
なお、しんかい6500は、ある深さまでは等加速度運動をしてから等加速度運動に運動の状態が変化したことから、水中で停止せずに沈んでいきます。
（6）①
解答：1.0N
解説：
ばねが無いので、円柱Bには重力と浮力がはたらき、釣り合っています。
（6）②
解答：1.9N
解説：
円柱B（1個1.0N）が1個、円柱C（1個0.30N）が3個あるので、一体となった物体全体にはたらく重力の大きさは、1.0N×1＋0.30N×3＝1.90N
問題文に「小数第1位まで書くこと。」とあるので、1.9Nが答えになります。
（6）③ ★やや難
解答：1.8N
解説：
（4）aの考察より、底面積20cm2の円柱において、水面から円柱の底面までの長さが2.0cm増えるごとに、浮力の大きさは0.4Nずつ増えていきます。
円柱Bと円柱Cはともに底面積が20cm2と同じであり、円柱Bの高さは6.0cm、円柱C3個の高さは1.0cm×3＝3.0cmから、合計9.0cmです。
よって浮力の大きさは、(0.4N/2.0cm)×9cm＝3.6/2＝1.8N。
（7） ★やや難
解答：鉄のおもりの一部を切り離すことで、浮力と重力がつり合うようにしている。
解説：
問題文より、しんかい6500には、鉄のおもりが複数個船体に取り付けられています。
図4の状態では、しんかい6500に見立てた円柱の物体は、「浮力＜重力の大きさ」であるため、等加速度運動をして、沈んでいきます。
しかし、一定の深さになると「浮力＋動きをさまたげる力＝重力の大きさ」となるため、等速直線運動をします。力は釣り合っていますが初速がゼロでないため、一定の速度で沈んでいきます。しんかい6500はすべて沈んでいるので、浮力の大きさは一定です。
ここで、しんかい6500の鉄のおもりの一部を切り離すことで、重力の大きさが小さくなります。
しかし、しんかい6500は一定時間は沈むため、動きをさまたげる力の大きさは変わらず、一時的に「浮力（一定）＋動きをさまたげる力＞重力の大きさ」となり、やがて停止します。
しんかい6500が停止すると、動きをさまたげる力の大きさはゼロになるので、「浮力＝重力の大きさ」となって、水中に停止します。
