こんにちは、個別指導塾まさです。
今回は、2023年(令和5年)に行われた、高専入試「理科」の問題・解答・詳しい解説を公開致します。
オンライン個別指導塾と家庭教師をやっています。北大院卒、指導経験20年以上。当塾は中上位高校志望の子が多いですが、勉強が苦手な子も多数在籍しています。今の学力は不問ですので、気軽にお申し込みください。授業料は1回70分 3,000円〜です。
＞＞教師紹介・料金・授業内容
＞＞体験授業かんたんお申し込み
＞＞お問い合わせ
★高専入試オススメ過去問題集★
高専入試「理科」(2023年・令和5年)問題・解答・解説
大問1 小問集合 ★問2がやや難
問1
解答：ア･･･2、イ･･･0
解説：
340m/s×6.0s＝34×6×10＝2040m＝2.04km
問題文で「何km離れていると考えられるか」とあるので、整数部分を答えて、2.0kmとなります。
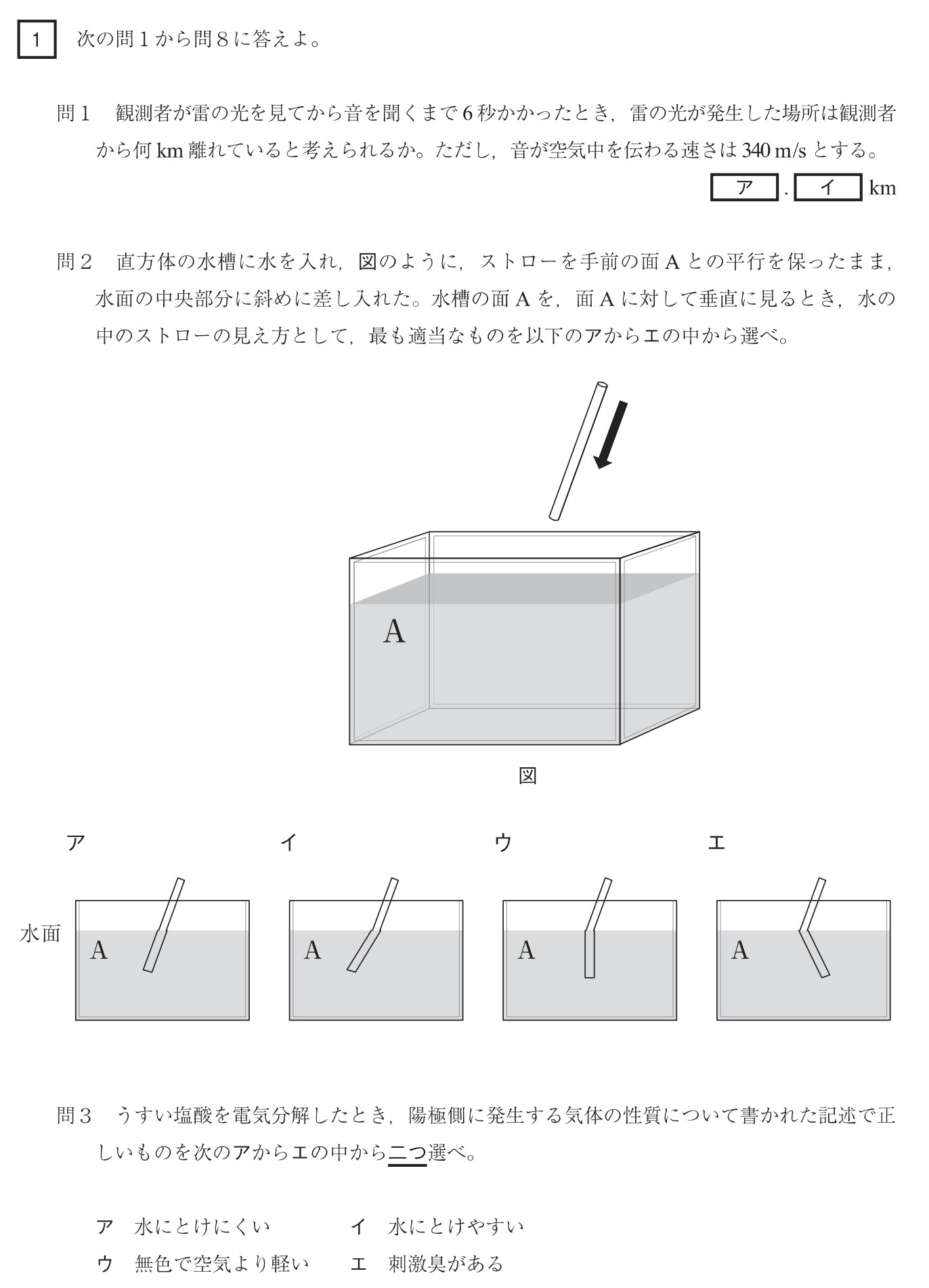
問2 ★やや難
解答：ア
解説：
ストローが反射した光がA面に向かうとき、光がガラスから空気に出るときに、ガラスの方が密度が大きいので、入射角＜屈折角となるように屈折します。
ストローが反射した光が、水槽の空気→水槽のガラス→空気のときよりも、水槽の水→水槽のガラス→空気のときの方が屈折角の差が大きくなるので、選択肢アのように見えます。
選択肢イは、図の水槽を真上から見たときのストローの見え方です。
問3
解答：イ、エ
解説：
電離式は、HCl→H+＋Cl–、よりCl–が陽極へ行き電子を放出してCl2になります。
気体の塩素（Cl2）の性質は、水にとけやすいこと、水溶液は漂白作用があること、刺激臭があること、などがあります。
問4
解答：イ
解説：
ア：状態変化です。
イ：例えば亜鉛にうすい塩酸を加えると、亜鉛がとけて塩化亜鉛に変化します。化学変化は物質と化合する原子の相手が変わり、別の物質に変化する反応なので、選択肢イは化学変化です。
ウ：砂糖の粒子が水中で拡散したのみで、別の物質に変化していないので化学変化ではありません。
エ：状態変化です。
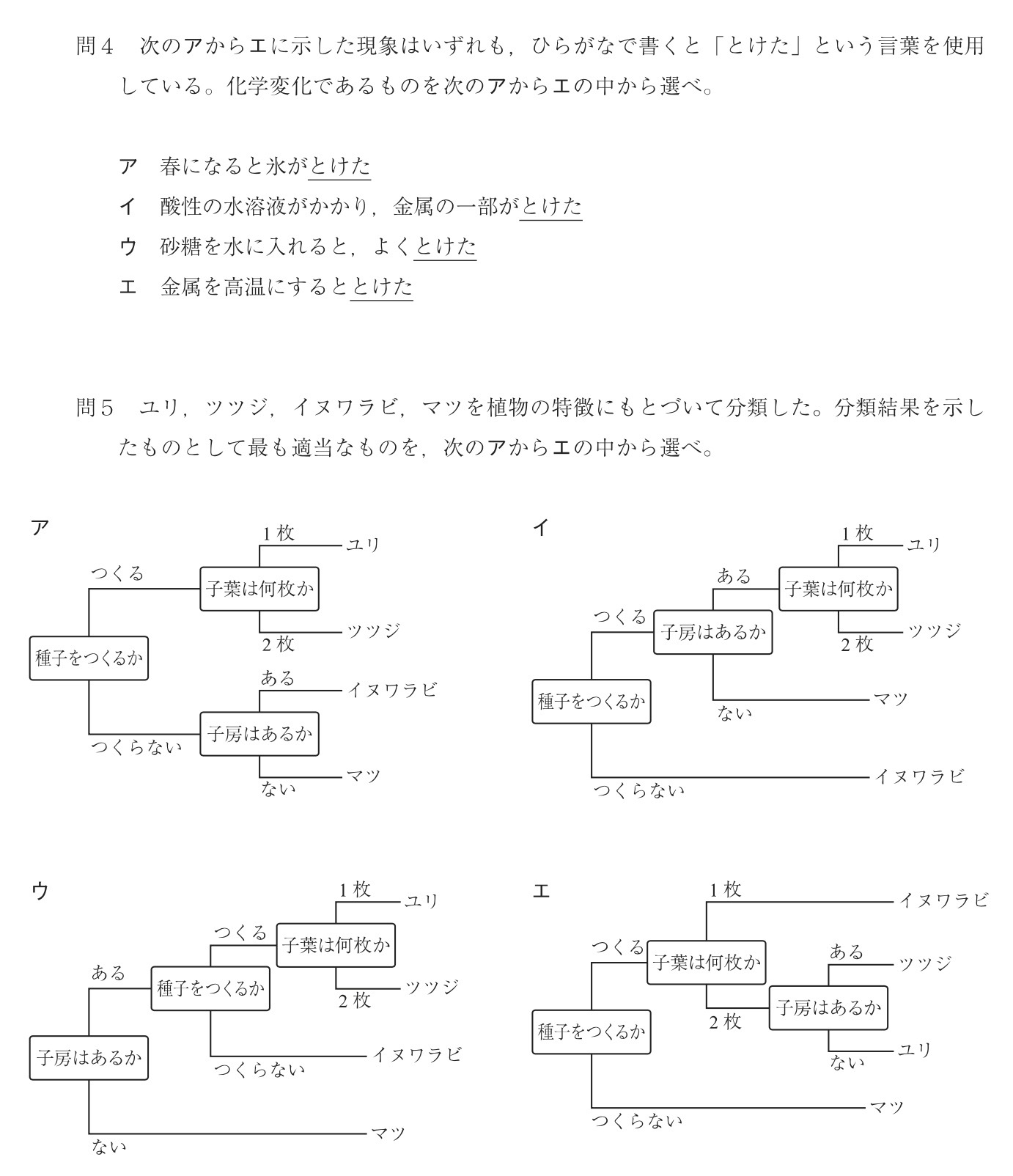
問5
解答：イ
解説：
ユリは単子葉類（種子をつくり、子葉が1枚の植物）です。→選択肢エは不適
ツツジは双子葉類の合弁花類（種子をつくり、子葉が2枚で、花弁がくっついている植物）です。
イヌワラビはシダ植物（種子をつくらず胞子で増える植物）です。→選択肢ア、ウは不適なので、選択肢イが正解。
マツは裸子植物（種子をつくり、胚珠が子房に包まれていない植物）です。
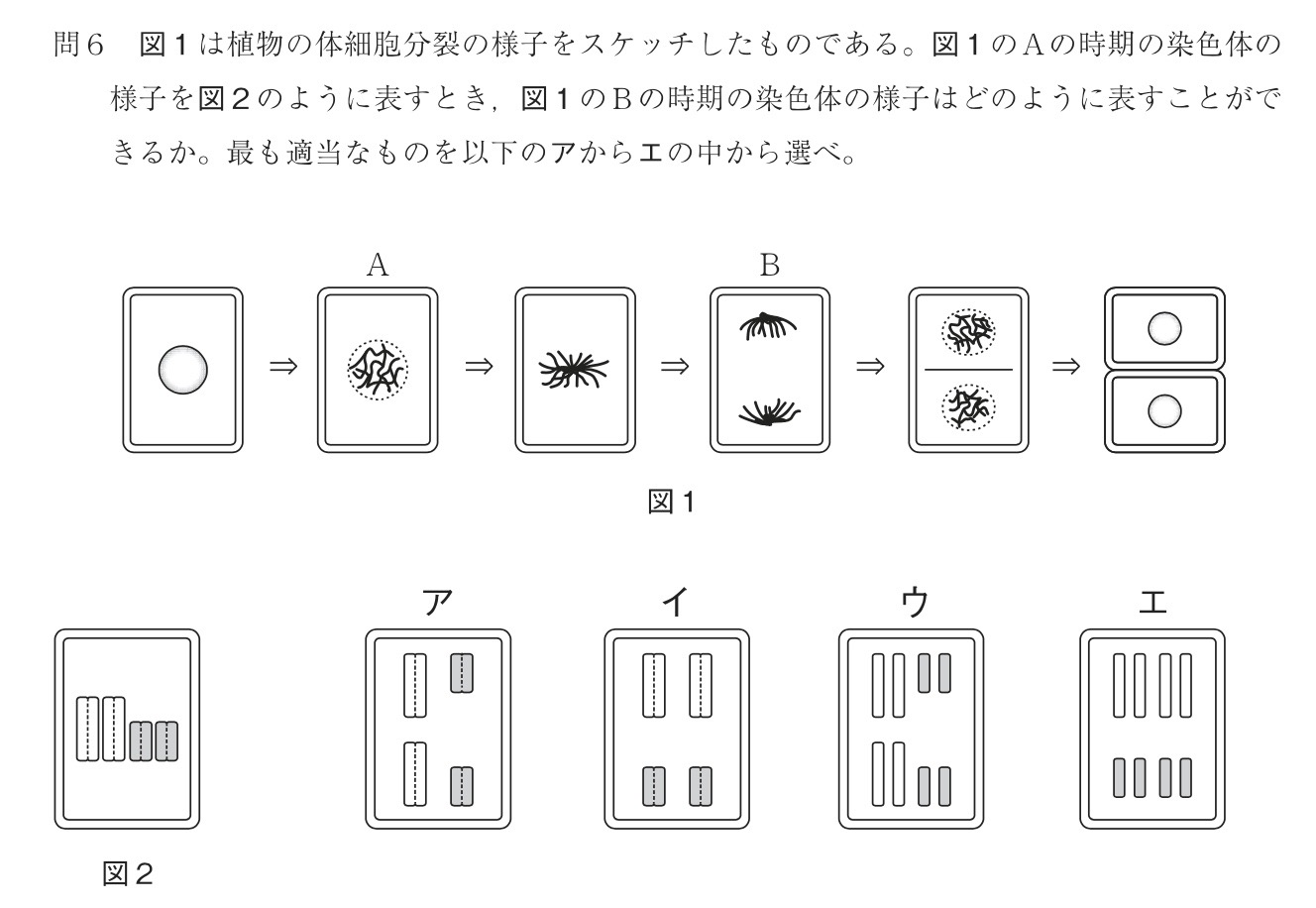
問6
解答：ウ
解説：
体細胞分裂において、Aは染色体が2倍に複製された状態で、Bは染色体が上下に半分ずつ分かれた状態です。
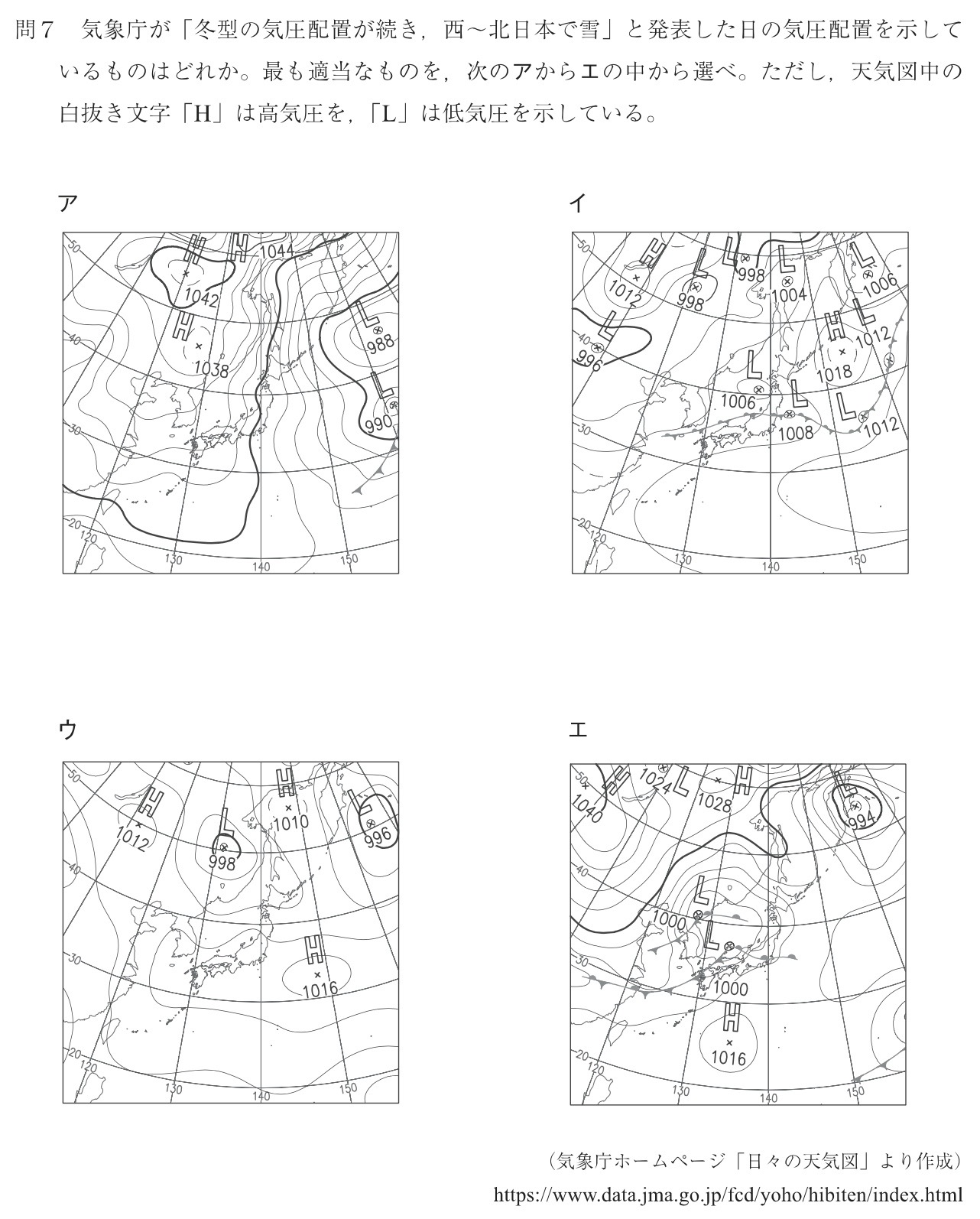
問7
解答：ア
解説：
冬型の気圧配置は、西高東低で、等圧線が縦縞になっています。これより、選択肢アが正解です。
選択肢イは日本列島に停滞前線があるので、春から夏、夏から秋にかけて見られる気圧配置です。
選択肢ウは南高北低の気圧配置なので、夏の気圧配置です。
選択肢エは移動性高気圧と低気圧が日本列島を交互に通過しているので、春または秋の気圧配置です。
問8
解答：①･･･ア、②･･･キ
解説：
地震の発生場所は震源、震源の真上の場所は震央です。
地震の規模はマグニチュード、ゆれの強さは震度です。
スポンサーリンク
大問2 植物の光合成と蒸散 ★問2と問3がやや難
問1
解答：ア、ウ
解説：
気孔からは、二酸化炭素（CO2）が入り酸素（O2）と水蒸気（H2O）が出ていきます。
光合成により二酸化炭素が入り酸素が出て行き、呼吸により酸素が入り二酸化炭素が出て行きます。
水蒸気は蒸散により出て行きます。
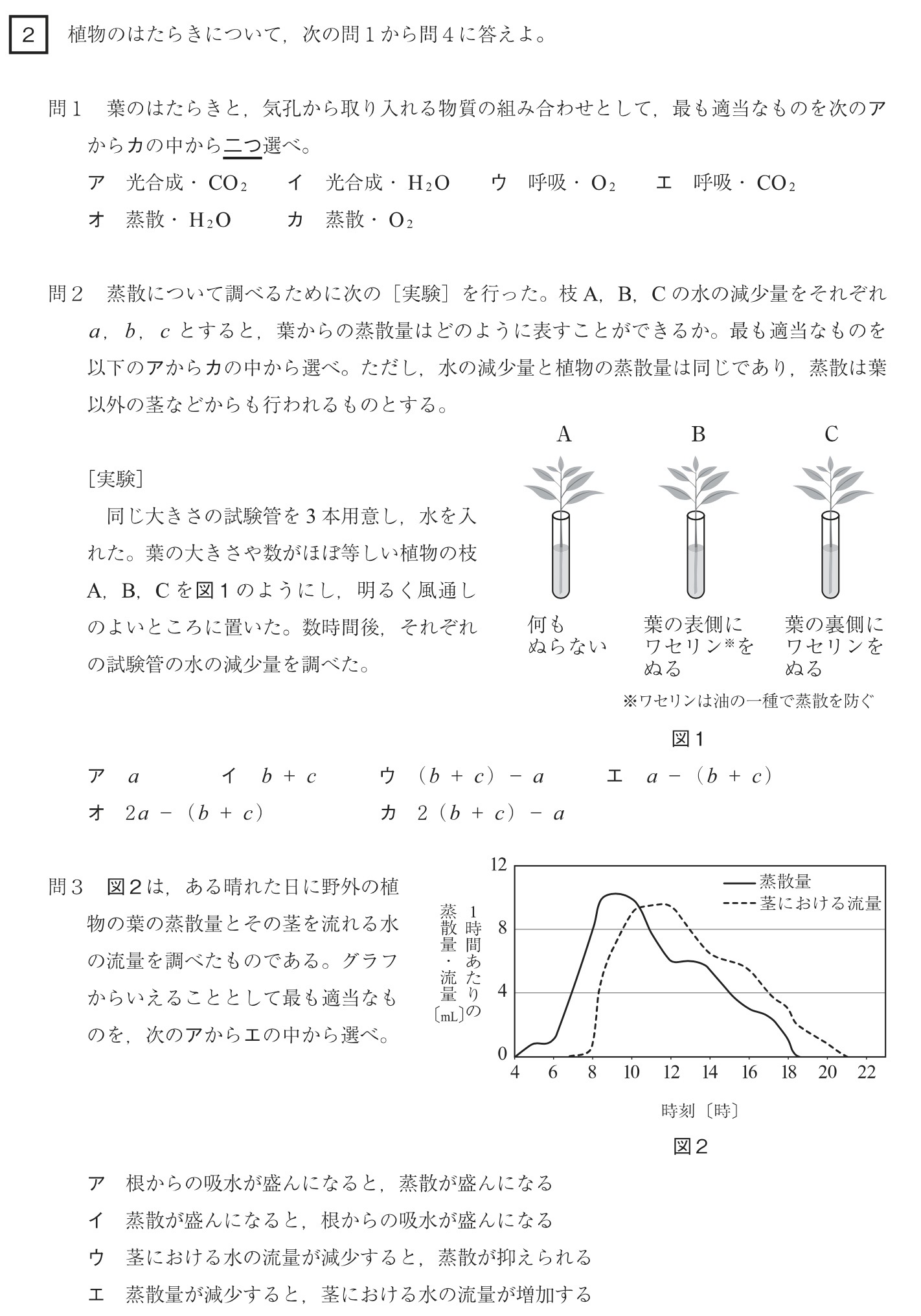
問2 ★やや難
解答：オ
解説：
a＝葉の表＋葉の裏＋茎
b＝葉の裏＋茎
c＝葉の表＋茎
これより、葉の表と葉の裏からの蒸散量は、
葉の表＝a（葉の表＋葉の裏＋茎）-b（葉の裏＋茎）
葉の裏＝a（葉の表＋葉の裏＋茎）-c（葉の表＋茎）
よって、葉からの蒸散量は、
葉からの蒸散量＝葉の表＋葉の裏＝（a-b）＋（a-c）＝2a – b – c＝2a +（b+c）
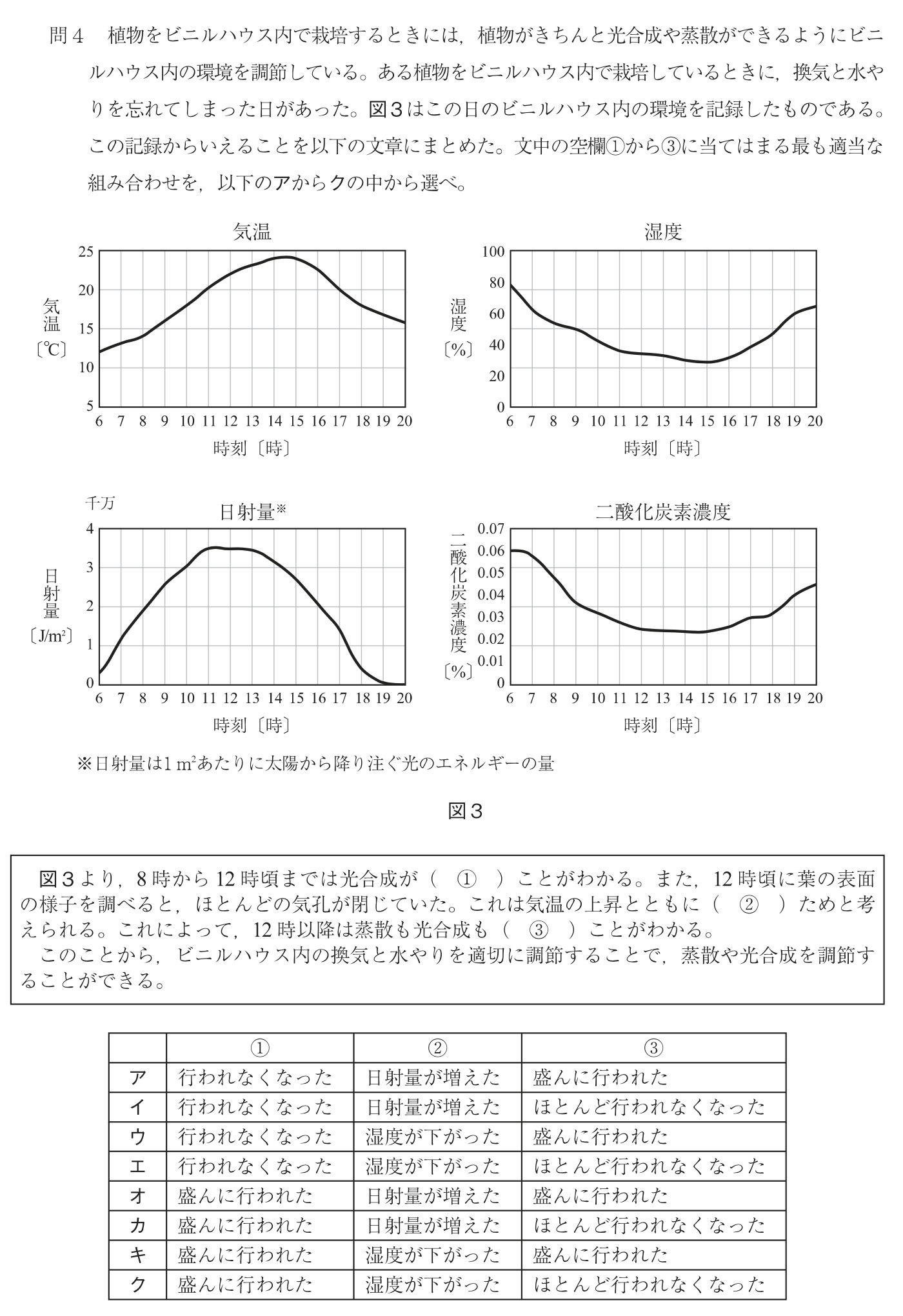
問3 ★やや難
解答：イ
解説：
ア：10時〜13時頃は茎における流量が最大ですが、蒸散量は減少しているので不適です。
イ：正しい。グラフの10時以前では、蒸散量が増加すると少し遅れて茎における流量が増加しているので、蒸散が盛んになると根からの吸水が盛んになると考えられます。
ウ：グラフの10時以降では、蒸散量が減少すると少し遅れて茎における流量が減少しているので、蒸散が抑えられると茎における水の流量が減少すると考えられます。
エ：選択肢ウの考察より、不適です。
問4
解答：ク
解説：
図3の日射量のグラフより、8時から12時頃までは日射量が増加して12時で最大になっているので、光合成が盛んに行われたと考えられます。
12時頃はほとんどの気孔が閉じていたこと、図3の湿度と二酸化炭素濃度のグラフより12時頃は湿度と二酸化炭素濃度が最小であること、気温のグラフから12時頃は気温が最大であることから、気温の上昇とともに蒸散も光合成もほとんど行われなくなったことが分かります。
その原因は、図3の日射量のグラフより、12時頃は日射量が最大であることから、日射量が増えたからであると考えられます。
スポンサーリンク
大問3 斜面上の物体の運動 ★問5がやや難、問6が難
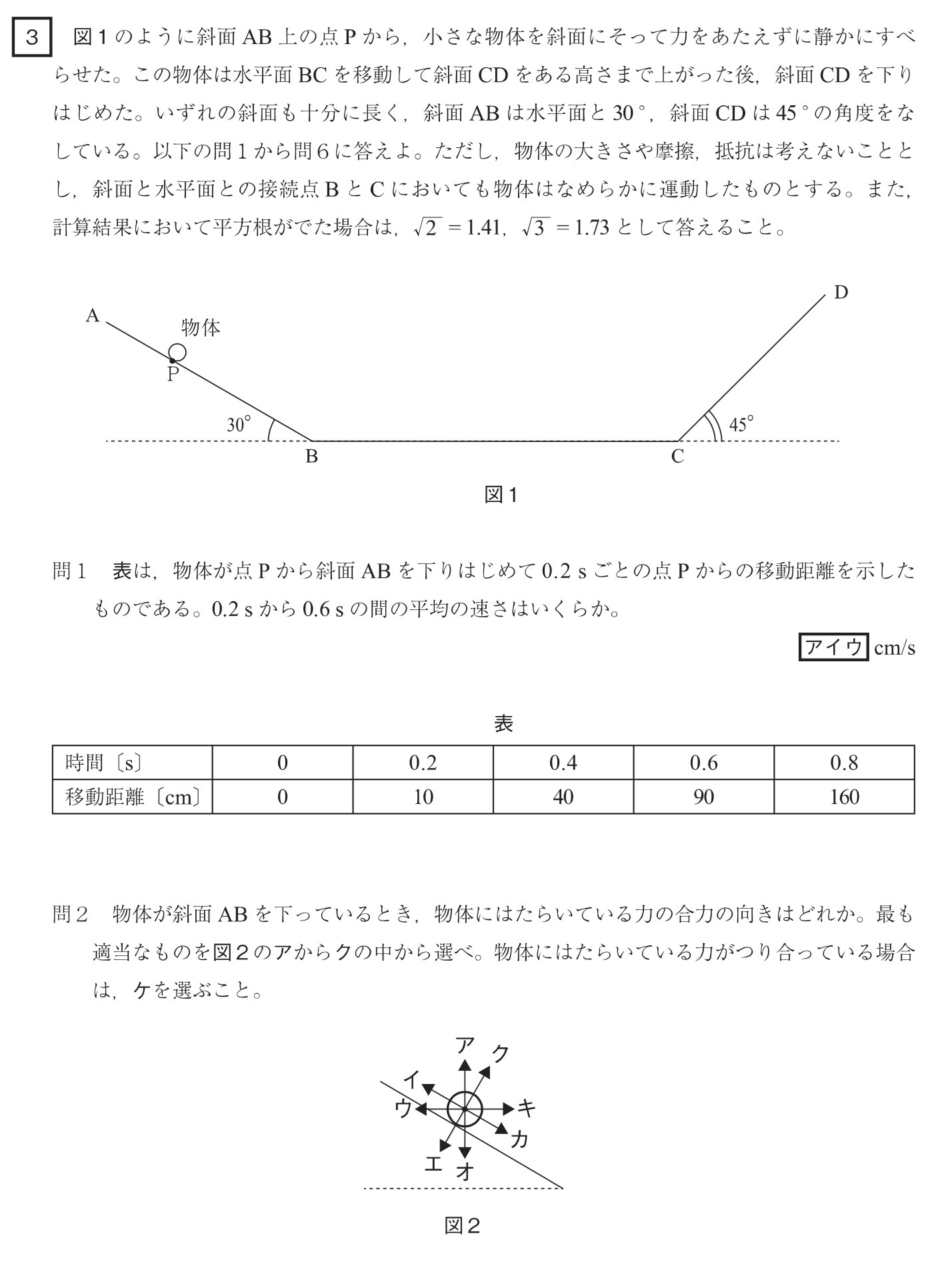
問1
解答：ア･･･2、イ･･･0、ウ･･･0
解説：
0.4s間（0.6s-0.2s）で80m（90m-10m）移動したので、
平均の速さ＝80m/0.4s＝800/4＝200m/s
問2
解答：カ
解説：
物体には重力がオの向きに働きます。
重力は、物体にはたらく重力の斜面方向の分力（カ）と斜面と垂直方向の分力（エ）に分解できます。
問題文に「斜面と水平面との接続点BとCにおいても物体はなめらかに運動したものとする。」とあるので、斜面方向においては、斜面方向の分力（カ）のみはたらくので、物体は斜面を下る等加速度運動をします。
斜面と垂直方向の分力（エ）は物体にはたらく垂直抗力（ク）とつり合うので、斜面と垂直方向には物体は運動しません。
以上より、物体にはたらく合力はカのみです。
問3
解答：ケ
解説：
物体には重力がオの向きに働きます。
重力（オ）は物体にはたらく垂直抗力（ア）とつり合います。
問題文に「斜面と水平面との接続点BとCにおいても物体はなめらかに運動したものとする。」とあるので、物体の進行方向には力がはたらきません。しかし物体が斜面ABを下った後も動いているので、物体は等速直線運動をします。
以上より、物体にはたらく力の合力はゼロ（ケ）です。
問4
解答：エ
解説：
物体には重力がオの向きに働きます。
重力は、物体にはたらく重力の斜面方向の分力（エ）と斜面と垂直方向の分力（カ）に分解できます。
問題文に「斜面と水平面との接続点BとCにおいても物体はなめらかに運動したものとする。」とあるので、斜面方向においては、斜面方向の分力（エ）のみはたらくので、物体は速さが一定の割合で減少する等加速度運動をします。
斜面と垂直方向の分力（カ）は物体にはたらく垂直抗力（イ）とつり合うので、斜面と垂直方向には物体は運動しません。
以上より、物体にはたらく合力はエのみです。
問5 ★やや難
解答：ア･･･0、イ･･･7、ウ･･･1
解説：
力学的エネルギー保存の法則より、P点における位置エネルギーとQ点における位置エネルギーは同じなので、P点とQ点での水平面からの高さは等しいです。
よって、P点とQ点での水平面からの高さを1とすると、点Pから点Bまでの距離は2、点Cから点Qまでの距離は√2であるので、
CQ/PB＝√2/2＝1.41/2＝0.705≒0.71
⇔CQ＝0.71×PB
よって、点Cから点Qまでの距離は点Pから点Bまでの距離の0.71倍です。
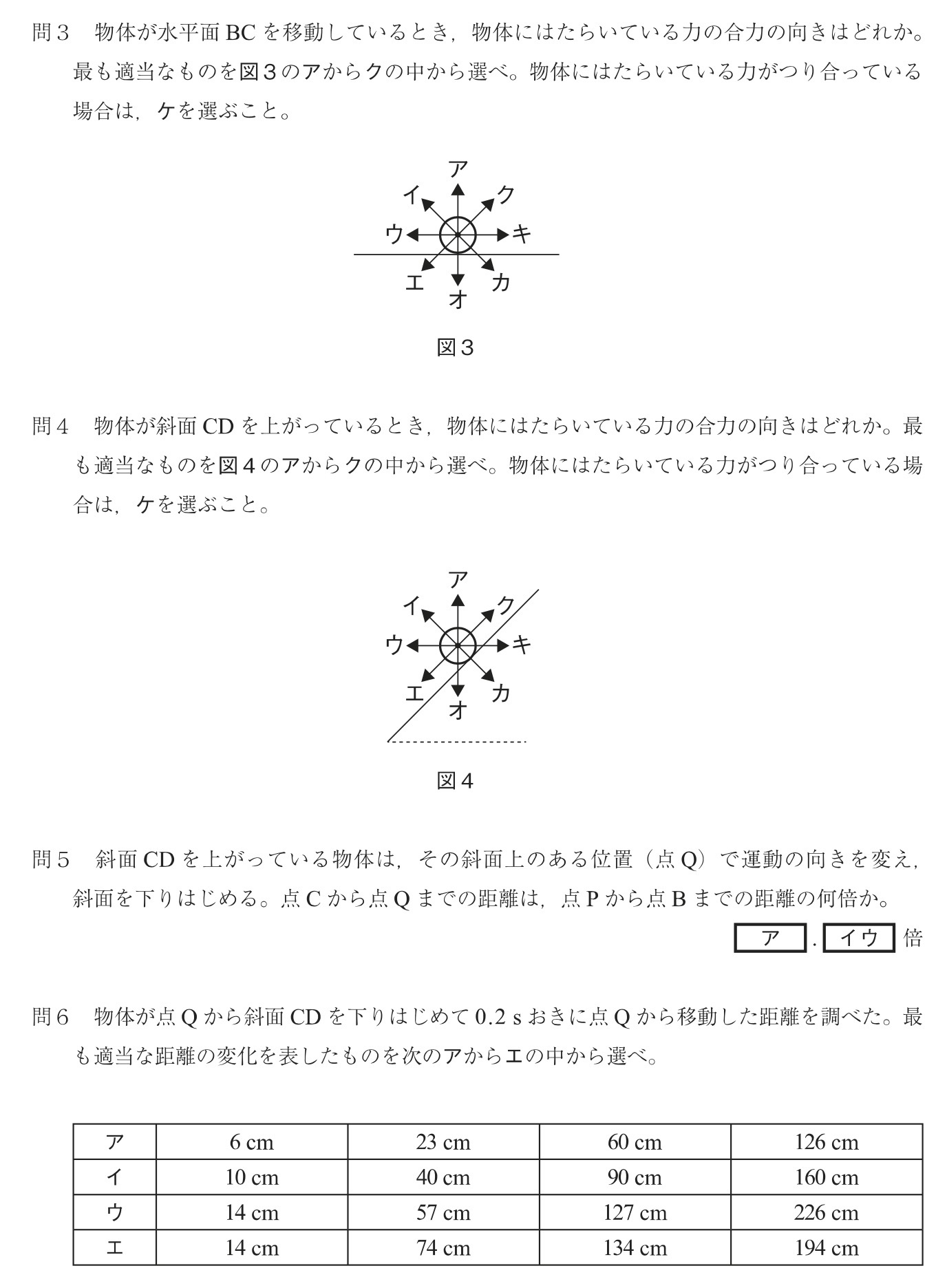
問6 ★難
解答：ウ
解説：
中学理科のレベルを超えた難問です。
物体の加速度をa、質量をm、物体にはたらく力の大きさをFとすると、運動方程式は、F＝ma ⇔ a＝F/m、と表すことができます。
条件より物体の質量は一定なので、斜面ABと斜面CDにおける物体にはたらく重力の斜面方向の分力の比が加速度の比となります。
物体が斜面ABを下るときの斜面方向の分力の大きさFABは、
FAB＝重力×（高さ/斜辺）＝重力×1/2
物体が斜面CDを上るときの斜面方向の分力の大きさFCDは、
FCD＝重力×（高さ/斜辺）＝重力×1/√2
よって加速度の比は、
aAB：aCD＝FAB/m：FCD/m＝FAB：FCD＝1/2：1/√2＝√2：2 ⇔ aCD＝2/√2×aAB＝√2×aAB＝1.41×aAB
加速度の単位[m/s2]より、物体の移動距離L[m]は、加速度a[m/s2]と移動時間t[s]を用いて、
L＝a×t2
よって、移動距離の比は加速度の比となるので、
LAB：LCD＝aAB：aCD＝aAB：1.41×aAB＝1：1.41 ⇔ LCD＝1.41×LAB
上式より、斜面CDを下ったときの移動距離は、斜面ABを下ったときの移動距離の1.41倍となります。
t＝0.2sのとき、斜面ABを下ったときの移動距離＝10cmより、斜面CDを下ったときの移動距離＝10cm×1.41＝14.1≒14cm
t＝0.4sのとき、斜面ABを下ったときの移動距離＝40cmより、斜面CDを下ったときの移動距離＝40cm×1.41＝4×14.1＝56.4≒57cm
t＝0.6sのとき、斜面ABを下ったときの移動距離＝90cmより、斜面CDを下ったときの移動距離＝90cm×1.41＝9×14.1＝126.9≒127cm
t＝0.8sのとき、斜面ABを下ったときの移動距離＝160cmより、斜面CDを下ったときの移動距離＝160cm×1.41＝16×14.1＝16×（14＋0.1）＝224＋1.6＝225.6≒226cm
以上より、答えは選択肢ウです。
大問4 月と金星
問1
解答：①･･･ウ、②･･･カ
解説：
月は地球の周りを公転する衛星です。
月食は満月のときに起こるので、太陽-地球-月の順番で一直線に並んだときに起こります。
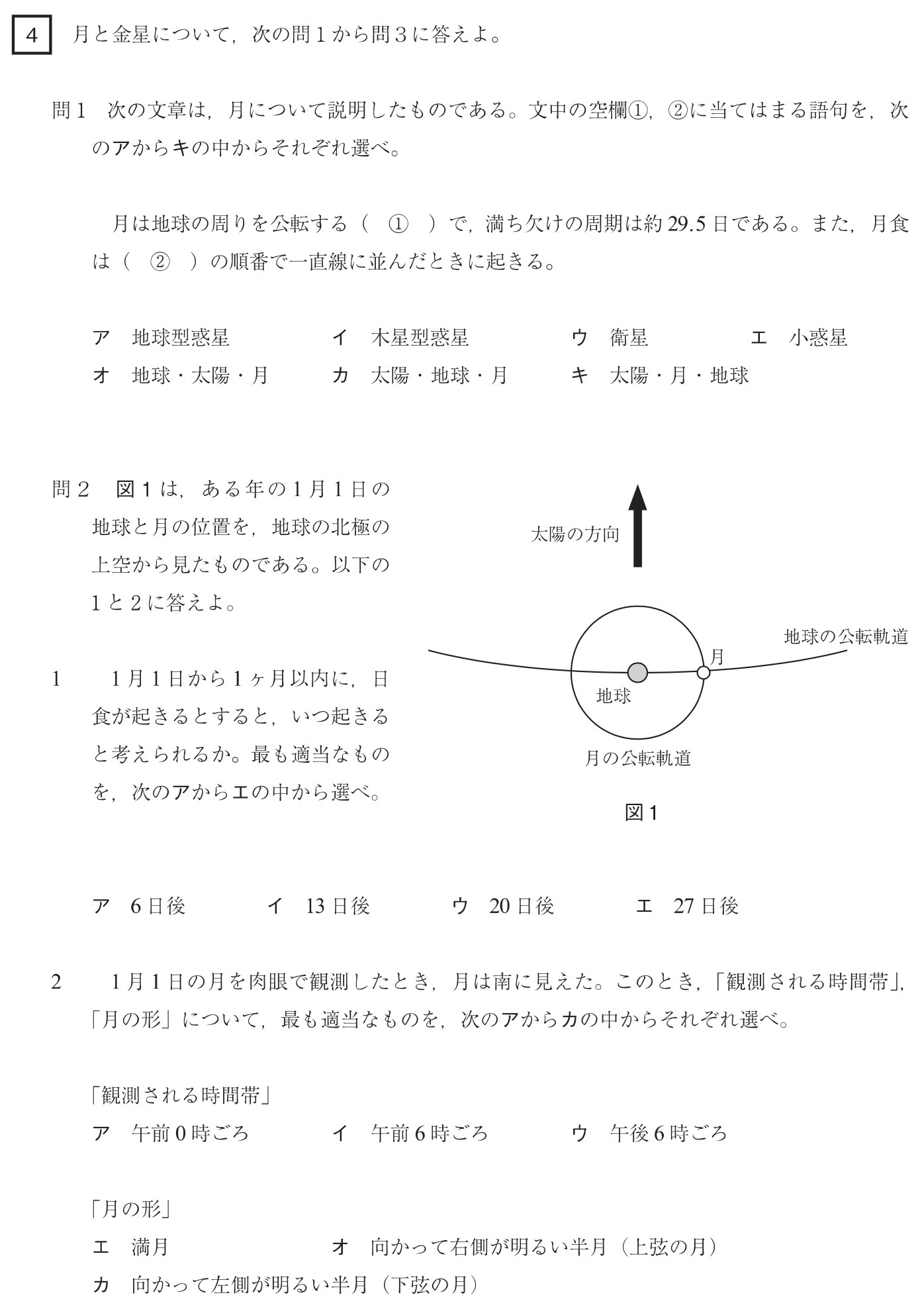
問2-1
解答：ア
解説：
日食は、太陽-月-地球の順番で一直線に並んだときに起こります。
図1では月は下弦の月の状態なので、ここから1/4周公転すると、日食が起こります。
月の自転・公転周期は約27.3日より、約27.3日×1/4≒6日後に日食が起こると考えられます。
問2-2
解答：観測される時間帯･･･イ、月の形･･･カ
解説：
月が南に見えたことから、地球上の明け方（午前6時ころ）に観測したことが分かります。
図1では月は左側が光った下弦の月の状態です。
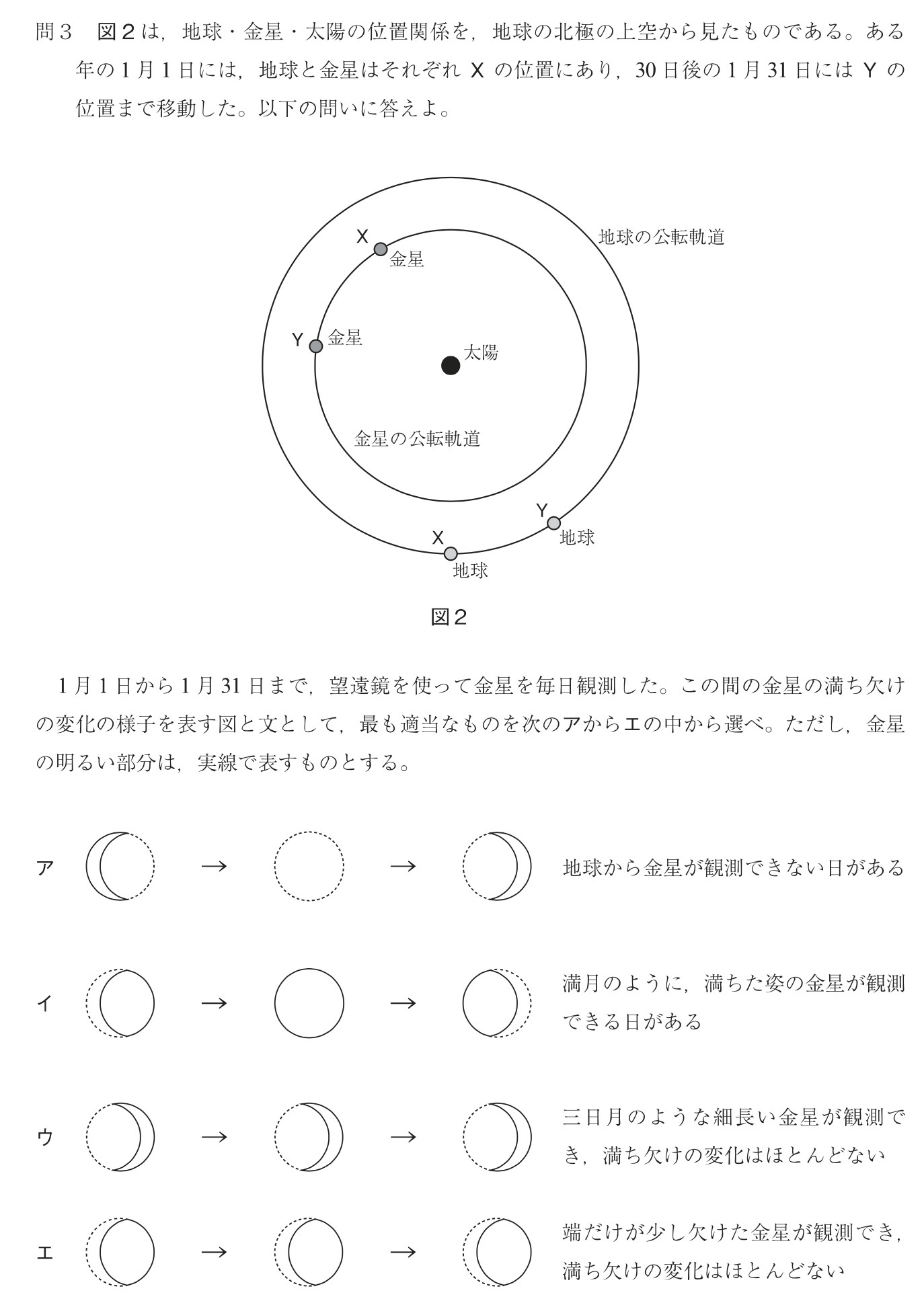
問3
解答：エ
解説：
地球と金星がXの位置にいるとき、肉眼で見ると金星は左側が少し欠けた形をしています。
（※この段階で選択肢イまたはエに絞られますが、選択肢イとエの金星は肉眼で見たときの状態です。しかし問題文に「望遠鏡を使って金星を毎日観測した。」とあるので、肉眼で見たときと上下左右が逆向きに見えるはずです。ここでは、選択肢の図が正しいものとしてはなしを進めます。）
地球と金星がYの位置にいるとき、Xの位置にいたときよりも金星は地球に少し近づいているので、金星は左側がXの位置にいたときよりも少し欠けた形をしています。
よって、正解は選択肢エです。
大問5 溶解度 ★問2がやや難
問1
解答：エ
解説：
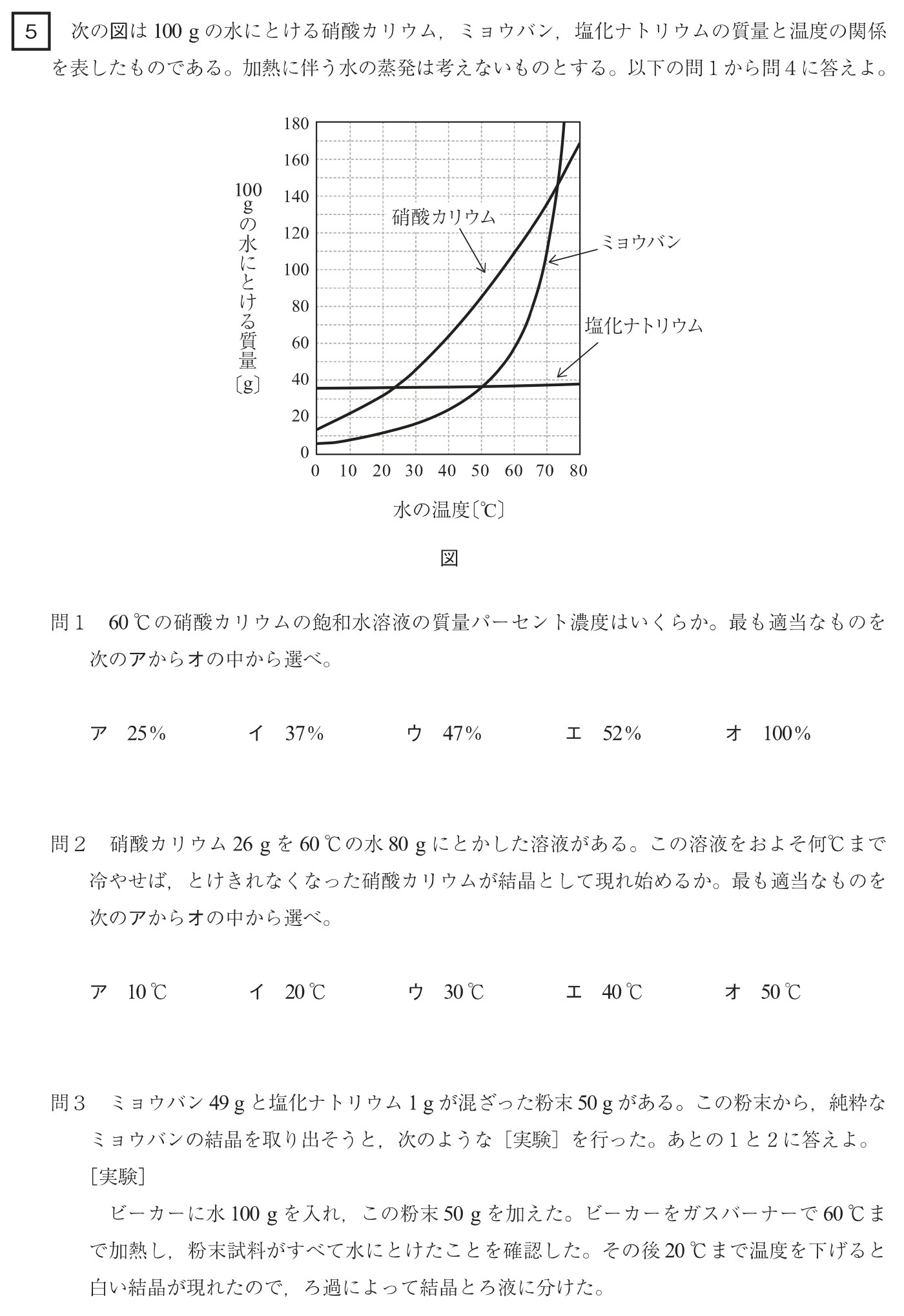
図より、60℃の水100gに硝酸カリウムは約110gとけているので、質量パーセント濃度は、
110g÷（100g＋110g）×100＝110×100/210＝1100/21≒52％
問2 ★やや難
解答：イ
解説：
水100g＝水80g×100/80＝80g×5/4より、60℃の水100gに硝酸カリウムを26g×5/4＝130/4＝32.5gとかしたと仮定します。
図より、硝酸カリウムの溶解度が32.5g以下となるのは約20℃なので、この温度以下になると、硝酸カリウムの結晶が析出すると考えられます。
問3-1
解答：イ
解説：
単純な知識問題なので、解説略。
問3-2
解答：エ
解説：
図より、20℃におけるミョウバンの溶解度は約11g、塩化ナトリウムの溶解度は約35gです。
この問題では、水100gにミョウバン49gと塩化ナトリウム1gを加えています。
よって、水の温度を20℃まで下げると、ろ液にはミョウバンが11g、塩化ナトリウムが1g含まれているので、質量比は11：1です。
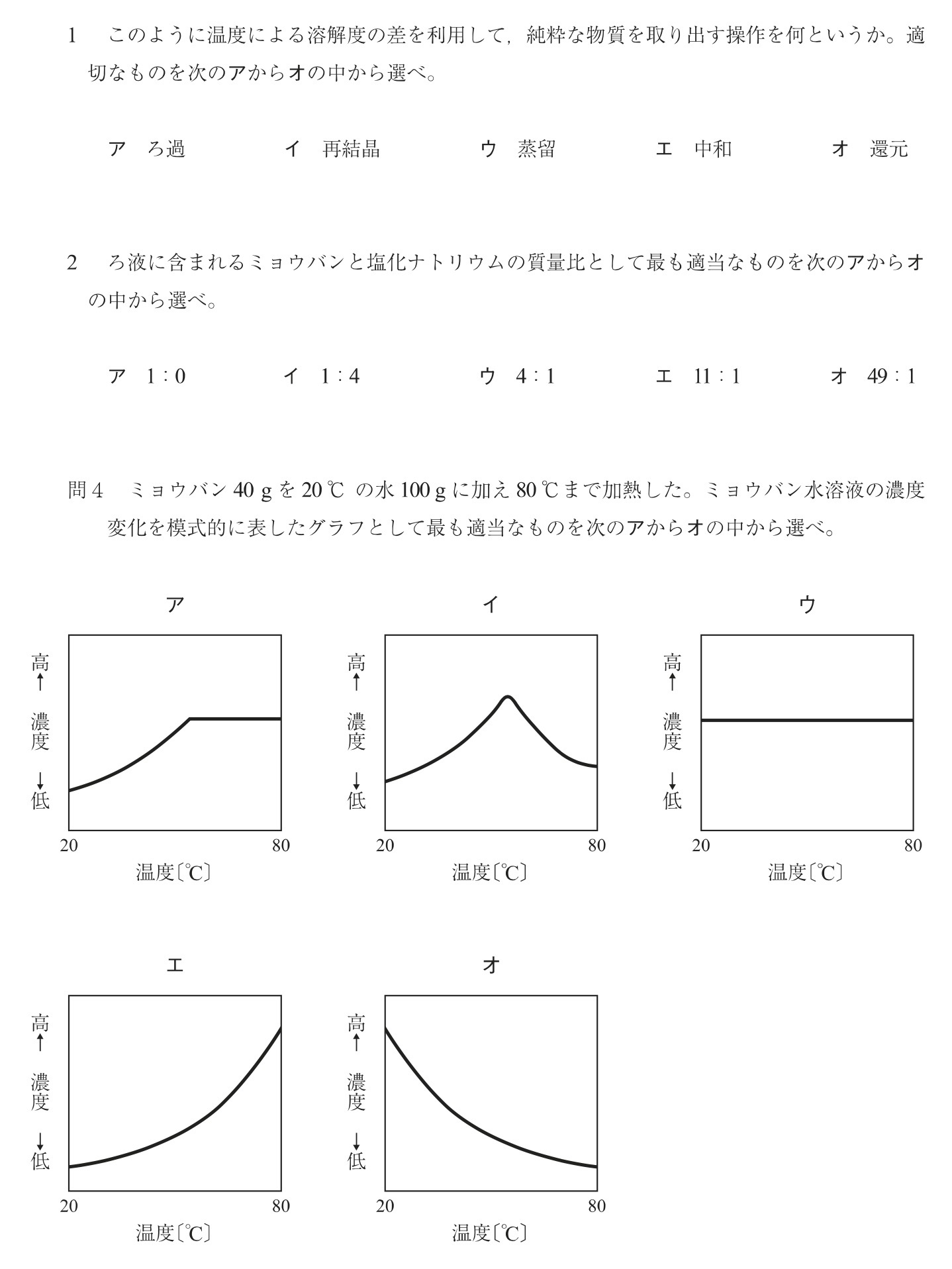
問4
解答：ア
解説：
質量パーセント濃度は、水にとけた溶質の質量のみを用いて計算します。
図より、20℃におけるミョウバンの溶解度は約11gなので、ミョウバン40gをとかすととけ残りが発生します。
20℃から温度を上げていくと、溶解度が上がっていきます。すなわち、質量パーセント濃度が増加していきます。
50℃を少し超えたあたりで溶解度が40gを超えるので、ミョウバン40gはすべてとけます。
温度を50℃より上げてもミョウバン40gはすべてとけた状態なので、質量パーセント濃度は増加しません。
以上より、答えは選択肢アです。
大問6 総合問題 ★問1と問3がやや難
問1 ★やや難
解答：ウ
解説：
大気中に含まれる気体（吸う空気）の割合は、窒素が約78％、酸素が約21％、二酸化炭素が約0.04％です。
はき出す空気（呼気）には、同様に窒素と酸素と二酸化炭素などが含まれています。
呼気には吸う空気よりも二酸化炭素が多く含まれていますが、窒素の割合を超えることはありえません。
よって、ヒトの呼気に最も多く含まれているのは窒素です。
選択肢アの分子モデルは二酸化炭素なので、●は酸素原子、中央の丸は炭素原子です。これより、選択肢エの分子モデルは酸素です。
選択肢イの分子モデルは水分子の形状であるので、○は水素原子です。
よって、窒素の分子モデルは選択肢ウです。
問2
解答：ア、エ
解説：
二酸化炭素を多く含んだ血液（静脈血）が流れる血管は、からだを循環して心臓に戻る血液が通る大静脈（エ）と、心臓から肺に送り出される血液が通る肺動脈（ア）です。
問3 ★やや難
解答：エ
解説：
問題文より、普通の空気（大気）での二酸化炭素は400ppmなので、1.0m3＝100×100×100cm3＝1000×1000cm3の空気のうち、400.0cm3分だけ占めています。
また、ヒトの呼気1L＝1000cm3に含まれる二酸化炭素は40mL＝40cm3より、ヒトの呼気1000×1000cm3のうち二酸化炭素は40cm3×1000だけ含まれています。
よって、大気中の二酸化炭素の体積の割合と比べて、およそ40cm3×1000÷400.0cm3＝100倍です。
問4
解答：ウ
解説：
単純な知識問題なので、解説略。
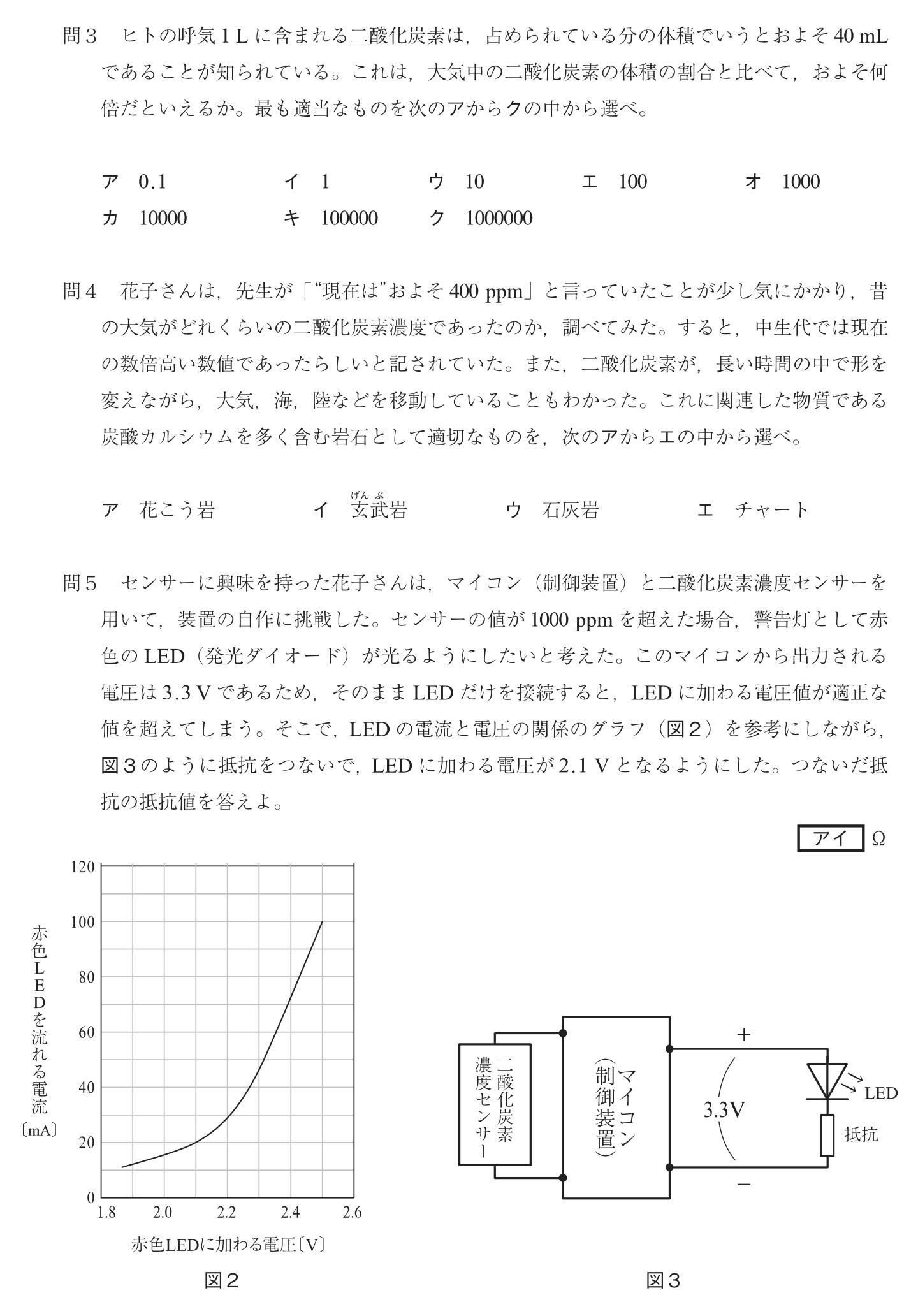
問5
解答：ア･･･6、イ･･･0
解説：
図3は直列回路より、抵抗に加わる電圧の大きさは3.3V-2.1V＝1.2Vです。
図2より、赤色LEDに加わる電圧の大きさが2.1Vのときの電流の大きさは20mAです。
以上より、オームの法則を用いて、抵抗の抵抗値は、
V＝IR ⇔ R＝V/I＝1.2V/20mA＝1.2×1000/20＝0.6×100＝60Ω
問6
解答：数値･･･オ、単位･･･ク
解説：
図4より、センサーの値が1000ppmを超えた時間は約30分＝30×60sです。
抵抗に加わる電圧の大きさは1.2V、抵抗値は60Ωより、発熱量Q[J]は
Q[J]＝V2t/R＝(1.2V)2×30×60s/60Ω＝1.44×30＝14.4×3＝(14+0.4)×3＝42+1.2＝43.2J（選択肢オ）
