👉教師紹介・料金
※授業料1回1,500円+交通費(コミコミ最大3,000円)・入会金なし・お好きな日時に受講・3回のお試し期間あり(無料教材あり)
☆学力テストはこれで完璧!オリジナル教材☆
👉北海道学力テストはこれで完璧!オリジナル教材+過去問一覧
※過去問の販売はできませんのでご注意ください。
大問1
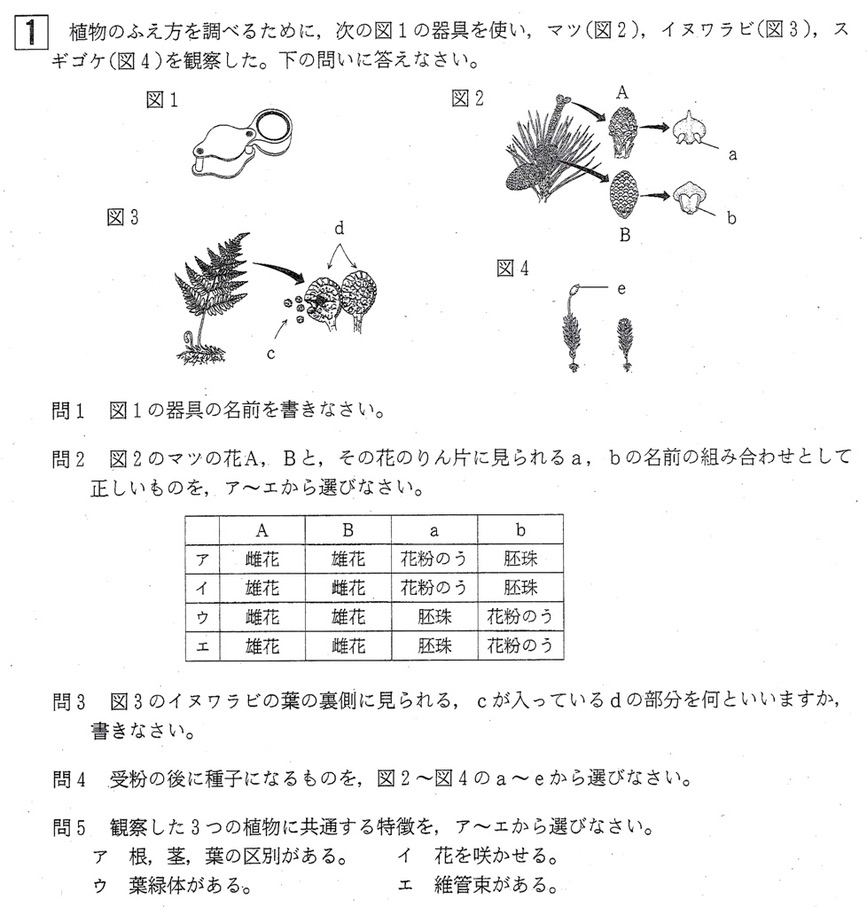
問1
解答:ルーペ
解説:
野外で植物などを観察するときは、ルーペを使います。
ルーペの使用手順は、以下の3つです。
①ルーペを目に近づけて持つ
②観察する試料をもう一方の手で持ち、試料を前後に動かしてピントを合わせる
③観察するものが動かせないときは、ルーペを目に近づけたまま自分が動いてピントを合わせる
問2
解答:ウ
解説:
種子で増える植物を種子植物といい、胚珠が子房で包まれている植物を被子植物、胚珠がむきだしの植物を裸子植物といいます。
アブラナのような被子植物は、受精後、胚珠は種子に、子房は果実に、受精卵は胚となります。
マツは、裸子植物です。
マツの種子のでき方について。
雄花(B)のりん片にある花粉のう(b)から花粉が風で飛び、雌花(A)のりん片にある胚珠(a)につき受粉します。
受粉後すぐに受精が起こらず、雌花は翌年の春まで花粉を守り、翌年の春から夏にかけて受精します。
受精後、胚珠は種子に、雌花はまつかさに成長します。子房が無いので果実はできません。
図2の雄花の側には1年前に受粉した雌花があり、図の左下にあるのはまつかさ(2年前に受粉した雌花)です。
問3
解答:胞子のう
解説:
植物はまず、種子で増えるか胞子で増えるかで大別され、種子で増える植物を種子植物といいます。
胞子で増える植物は、今度は維管束があるかどうか、または、根・茎・葉の区別かあるかどうかで大別され、
維管束がある植物をシダ植物、ない植物をコケ植物といいます。
イヌワラビはシダ植物です。
シダ植物の個体の増やし方は、
葉の裏にある胞子のう(d)が乾いて裂けて胞子(c)が飛び出て、胞子が発芽して前葉体となり、前葉体の造精器(雄器)から精子が雨の日に泳いで別の前葉体の造卵器(雌器)の卵までいき受精し、受精卵が成長し若いシダとなって増えます。
シダ植物は、無性生殖→有性生殖の順で個体を増やします。
スギゴケやゼニゴケはコケ植物です。
コケ植物は、雄株と雌株の区別があるものが多いです。
個体の増やし方は、図4のスギゴケですと、
雄株の雄器で精子が、雌株の雌器で卵が作られ、雨の日などに精子が雌器の卵まで泳いで受精し、受精卵が育つと雌器に胞子のう(e)ができて胞子がつくられ、胞子のうが破れて胞子が飛び散り、発芽・成長して雄株と雌株になります。
コケ植物は、有性生殖→無性生殖の順で個体を増やします。
図3のイヌワラビのからだのつくりですが、
シダ植物の根は、種子植物ほど発達していないひげ根、茎は、地中を横に走る地下茎、葉は、地上に出ている部分全体が1枚の葉(複葉という)で、葉の部分を葉身、葉を支える枝を葉柄といいます。
問4
解答:a
解説:
マツの種子のでき方について。
雄花(B)のりん片にある花粉のう(b)から花粉が風で飛び、雌花(A)のりん片にある胚珠(a)につき受粉します。
受粉後すぐに受精が起こらず、雌花は翌年の春まで花粉を守り、翌年の春から夏にかけて受精します。
受精後、胚珠(a)は種子に、雌花はまつかさに成長します。子房が無いので果実はできません。
問5
解答:ウ
解説:
図2のマツは種子植物なので、花を咲かせ、根・茎・葉の区別があり、維管束の区別があり、葉に葉緑体をもち、光合成を行います。
コケ植物は、雄株と雌株の区別があるものが多いです。
シダ植物とコケ植物の相違点について。
シダ植物は、根・茎・葉(維管束)の区別があり根(ひげ根)で水を吸収します。
コケ植物は、根・茎・葉(維管束)の区別がなく、からだの表面で水を吸収します。また、雄株と雌株に分かれていることが多いです。
シダ植物とコケ植物の類似点について。
種子ではなく胞子で増える、湿ったところで生育する、葉緑体を持ち光合成をする、雄器で作られた精子が泳ぐために受精には水が必要、の4つです。
大問2
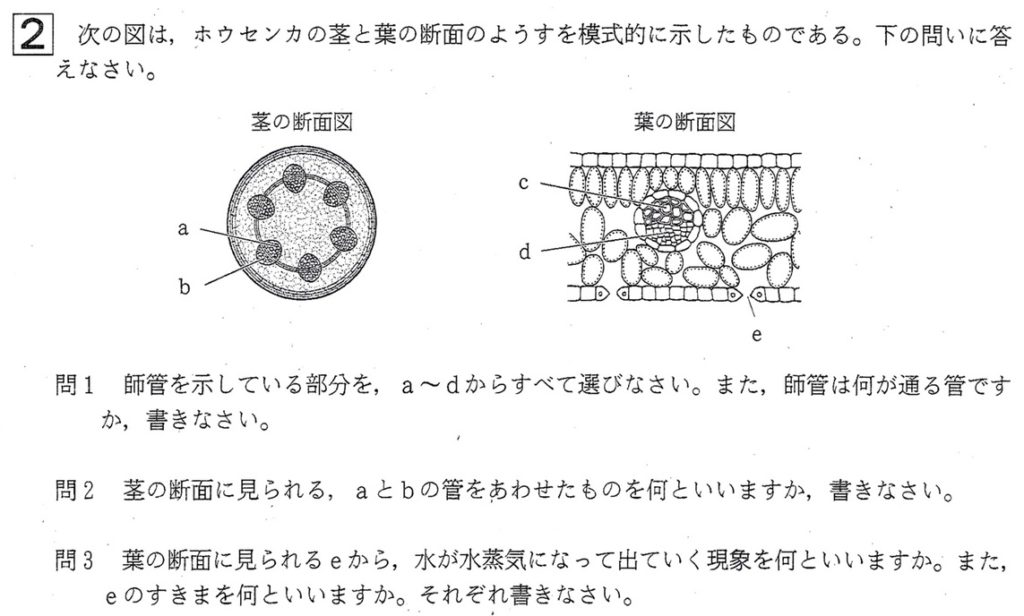
問1
解答: 師管:b、d 通るもの:栄養分(養分)
解説:
ホウセンカは双子葉類であることを覚えましょう。
双子葉類は、子葉が2枚、葉脈(葉の維管束)が網状脈、茎の維管束が輪状に並びます。
維管束とは、道管と師管の束のことです。
図の茎の断面図を見ると、双子葉類であるホウセンカの茎は、形成層があり、形成層を中心に維管束が輪状に並んでいます。
道管(a)は、根から吸収された水や肥料分が通る管で、茎では維管束の内側にあります。
双子葉類の根は、主根と側根からなり、根の先端ちかくに根毛があり、表面積を広げる構造をしており、これにより水や肥料分を効率よく吸収できます。
根で吸収された水は、茎の道管→葉の維管束である葉脈の道管→葉に送り届けられ、光合成の材料として使われます。
師管(b)は、葉で光合成で作られた養分(デンプン→ショ糖)が通る管で、茎では維管束の外側にあります。
葉の断面図においては、上から、表皮、柵状組織、維管束である葉脈、海綿状組織、表皮(裏側、気孔が多くある、e)、からなります。
植物の葉には葉緑体があり、光合成は葉緑体で行われます。
葉緑体は、柵状組織、海綿状組織、葉の裏側の孔辺細胞(孔辺細胞のすきまが気孔)にあります。
葉は光を受けやすく、光合成がさかんなため、柵状組織がぎっしりならびます。裏は気孔が多く、気体(酸素と二酸化炭素)が出入りしやすいように、海綿状組織がまばらに並びます。
葉の維管束を葉脈といいます。
茎の維管束では、内側が道管で外側が師管ですが、葉の維管束では、上側(表皮側)が道管(c)で下側が師管(d)です。
光合成は葉緑体で行われます。
根で吸収した水が茎の道管(維管束の内側)から葉の維管束である葉脈(維管束の上側)を通り葉緑体に届けられ、
孔辺細胞の隙間である気孔で吸収された二酸化炭素を日光(光エネルギー)を用いて、単糖類であるグルコース(ブドウ糖)と酸素に合成されます。
グルコースは水に溶けやすく、このままの形では葉に栄養分を貯蔵できないため、グルコースが多数つながった水に溶けにくいデンプンにつくり変えられます。
夜間に水に溶けやすい二糖類のスクロース(ショ糖)に変えられ、師管を通ってからだの各部へ運ばれて、呼吸や成長の材料として使われます。
問2
解答:維管束
解説:
問1解説参照。
問3
解答: 現象:蒸散、e:気孔
解説:
植物の葉の表、葉の裏、茎には気孔(孔辺細胞の隙間)があり、気孔から酸素や二酸化炭素が出入りし、水蒸気が出て行きます。
植物体内の水が、気孔から水蒸気となって体外に放出される現象を蒸散といいます。
蒸散がもつ3つのはたらき(メリット)は、
①体内の水分量の調節
②植物体の温度調節
→蒸散が起こると気化熱により植物体の温度が下がる
③水分移動の促進
→葉で蒸散が起こると植物体の水分量が減り、葉の細胞内液の濃度が高くなり、根から道管に水を押し上げる力である根圧と、葉が道管から水を吸収しようとする力である吸水力により、水分移動が促進される
大問3

問1
解答:A、E、F
解説:
植物の分類の観点はまず、種子をつくるか否かで大別します。
種子を作る植物を種子植物といいます。
種子植物はさらに、胚珠が子房に包まれているか否かで分類し、胚珠が子房に包まれている植物を被子植物、胚珠がむきだしの植物を裸子植物といいます。
被子植物はさらに、子葉の枚数で分類し、子葉が1枚の植物を単子葉類、子葉が2枚の植物を双子葉類といいます。
双子葉類はさらに、花弁がくっついているか否かで分類し、花弁がくっついている植物を合弁花類(ツツジ)、花弁が離れている植物を離弁花類(アブラナ)といいます。
単子葉類として、イネ・トウモロコシ・スズメノカタビラ・ユリ・アヤメ・ツユクサ・チューリップを、
合弁花類として、ツツジ・タンポポ・アサガオを、
離弁花類として、サクラ・アブラナ・エンドウを、
裸子植物として、マツ、スギ、ヒノキ、イチョウ、ソテツを
それぞれ覚えましょう。
これに加えて、ホウセンカは双子葉類であることも覚えましょう。
双子葉類は、子葉が2枚、葉脈(葉の維管束)が網状脈(F)、茎の維管束が輪状に並びます(E)。
維管束とは、道管と師管の束のことです。
道管は、根から吸収された水や肥料分が通る管で、茎では維管束の内側にあります。
師管は、葉で光合成で作られた養分(デンプン→ショ糖)が通る管で、茎では維管束の外側にあります。
双子葉類の根は、主根と側根からなり(A)、根の先端ちかくに根毛があり、表面積を広げる構造をしており、これにより水や肥料分を効率よく吸収できます。
単子葉類は、子葉が1枚、葉脈(葉の維管束)が平行脈(C)、茎の維管束が全体に散らばっています(B)。
双子葉類と同じく、茎では道管は維管束の内側に、師管は維管束の外側にあります。
単子葉類の根はひげ根(D)で、根の先端ちかくに根毛があり、表面積を広げる構造をしており、これにより水や肥料分を効率よく吸収できます。
問2
解答:ひげ根
解説:
問1解説参照。
問3
解答: ①面積、②水、③養分(肥料分)
解説:
問1解説参照。
大問4

問1
解答: 試験管:A、理由:葉で光合成が行われ、試験管の中の二酸化炭素が使われたから。
解説:
水道水はアルカリ性で、水酸化物イオン(OH–)のみ含まれています。
ヒトがはきだす空気は、16%が酸素、5%が二酸化炭素、78%が窒素です。
二酸化炭素は水に少しとける気体で、水に溶けると水素イオン(H+)を放出する酸です。
ゆえに、試験管にある水道水に息をふきこむと、水溶液中の水素イオン(H+)の量が増えて、アルカリ性が弱くなっていきます。
さらに息をふきこんでいくと二酸化炭素が多量に含まれた酸性の水溶液となっていきます。
石灰水に二酸化炭素を通すと、白く濁ります。
石灰水とは水酸化カルシウム(Ca(OH)2)のことです。
水酸化カルシウムは水溶液中に水酸化物イオン(OH–)があるので、アルカリ性です。
水酸化カルシウム水溶液に二酸化炭素(CO2)が溶けると炭酸(H2CO3)となり、水素イオン(H+)が放出されるので、酸性の性質を示します。
アルカリ性の水酸化カルシウムに、酸性の炭酸が加わることで中和が起こり、炭酸カルシウム(CaCO3)の塩が発生します。
炭酸カルシウムは白色の固体で、水にとけにくいため、水溶液中に拡散します。
石灰水が白く濁るのは、炭酸カルシウムが水溶液中に拡散しているためです。
この状態でさらに二酸化炭素を流すと、炭酸カルシウムは水に溶けやすい炭酸水素カルシウムとなり、水溶液は再び透明になります。
植物は光合成と呼吸を同時に行います。
光合成では、葉の気孔から、二酸化炭素が入り酸素が出ます。
呼吸では、葉の気孔から、酸素が入り二酸化炭素が出ます。
光の当たる場所では、光合成のはたらきの方が強くなるので、光合成で出入りする気体の量が、呼吸で出入りする気体の量より多くなり、あたかも酸素が放出されているかのように見えます。
光の当たらない場所では、呼吸のみ行われるので、二酸化炭素のみ放出されます。
ゆえに、試験管Cは、タンポポ(合弁花類)が呼吸のみ行い、水溶液は二酸化炭素が多量に含まれた酸性の水溶液なので、石灰水が白くにごります。
試験管Aは「じゅうぶんに日光を当てた」状況から、タンポポの葉からは、光合成で出入りする気体の量が、呼吸で出入りする気体の量より多くなるため、水溶液にある二酸化炭素が消費され、水溶液は再びアルカリ性に戻ります。
石灰水は二酸化炭素との中和反応で白く濁るので、二酸化炭素が存在しない試験管Aの水溶液に石灰水入れてふっても、白く濁りません。
試験管Bはタンポポの葉がないので、水溶液は二酸化炭素が多量に含まれた酸性の水溶液より、石灰水が白くにごります。
問2
解答:葉緑体
解説:
光合成は植物細胞の細胞質(原形質)にある葉緑体で行われます。
根で吸収した水が茎の道管(維管束の内側)から葉の維管束である葉脈(維管束の上側)を通り葉緑体に届けられ、
孔辺細胞の隙間である気孔で吸収された二酸化炭素を日光(光エネルギー)を用いて、単糖類であるグルコース(ブドウ糖)と酸素に合成されます。
グルコースは水に溶けやすく、このままの形では葉に栄養分を貯蔵できないため、グルコースが多数つながった水に溶けにくいデンプンにつくり変えられます。
夜間に水に溶けやすい二糖類のスクロース(ショ糖)に変えられ、師管を通ってからだの各部へ運ばれて、呼吸や成長の材料として使われます。
問3
解答:呼吸
解説:
問1解説参照。
光合成では、水と二酸化炭素が日光(光エネルギー)により、酸素とデンプンになります。
光エネルギーを受ける化学反応であるので、化学エネルギーが高い状態となります。
呼吸は、酸素と糖が分解され、生命活動の元として利用されるエネルギーが放出され、分解された糖は(有機物)は二酸化炭素と水になります。
この生命活動の元として利用されるエネルギーは、光合成で得た光エネルギーです。
呼吸ではエネルギーが放出されているので、二酸化炭素と水がもつ化学エネルギーは、酸素と糖より低くなります。
呼吸と光合成は、逆の関係にあるといえます。
大問5

問1
解答:光源
解説:
太陽や豆電球など自ら光を出すものを光源といいます。
光源が見えるのは、光源からの光が直接目に入るからで、光源以外のものが見えるのは、光源から出た光が物の表面で反射し、その光が目に入るからです。
図1や図2は、光があたかも一直線に進んでいるかのように見えますが、これはスリット(微少な穴)から出た光やレーザー光線を用いて光を一本線にして、分かりやすくしているだけです。
なお光は、さえぎるものがなければ同じ物質(空気やガラスなど)の中をまっすぐに進みます。これを光の直進といいます。
問2
解答: 入射角:b、反射角:38度
解説:
光は直進します。
直進した光が、鏡などの面に当たって反射するとき、入射角=反射角が成り立ちます。
これを反射の法則といいます。
鏡などの面に垂直な線のことを法線といいます。
入射角、反射角、屈折角は、法線とのなす角度です。
ゆえに、入射角はb、反射角はcで、b=cが成り立ちます。
a+b=90°より、b=90°-a=90°-52°=38°です。
反射角cは、反射の法則より、
b=c=38°です。
問3
解答:
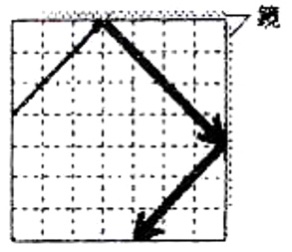
解説:
作図の問題は、必ず法線を書いてください。
図2の鏡に入射する光である入射光線を見ると、横に1マス進むと上に1マス進むので、傾きが1、すなわち入射角=45°で入射しています。
反射の法則より、反射角=入射角=45°です。
反射した光である反射光線は、合わせ鏡の右側に向かって、横に1マス進むと上に1マス進んで入射するので、同様に、射角=45°で入射しています。
反射の法則より、反射角=入射角=45°なので、反射光線は反射角45°で反射していきます。
問4
解答:(光の)反射(の法則)
解説:
問2解説参照。
大問6
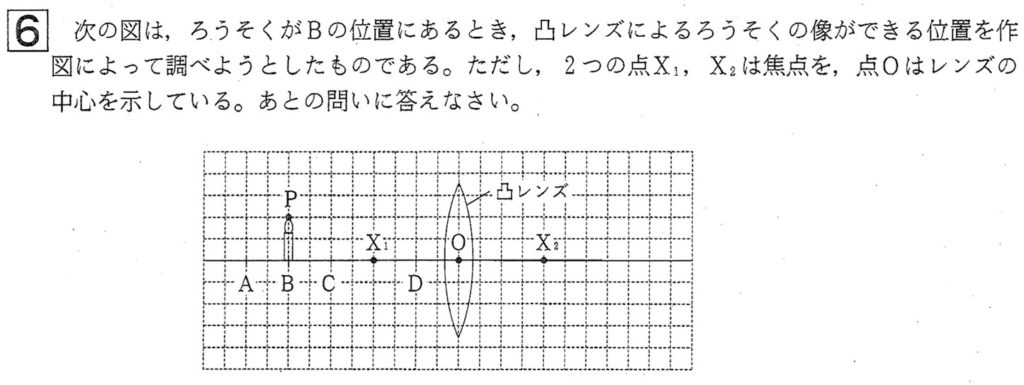

問1
解答:
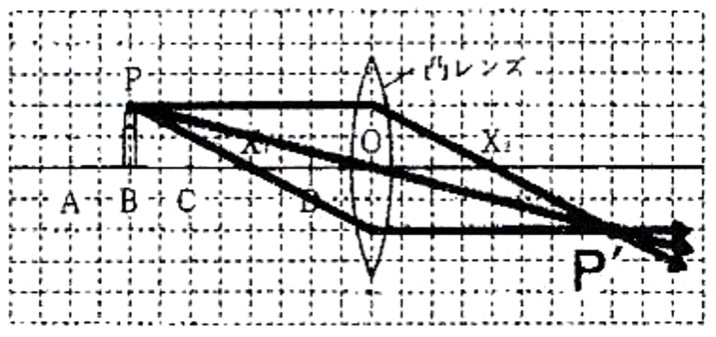
解説:
凸レンズとは、ガラス中央部分がまわりよりも厚いレンズのことです。
凸レンズに平行光線が入射すると、レンズの中心を通る光はそのまま直進し、それ以外の光はレンジに入射するときと出るときの2回屈折しますが、作図するときは、レンズの中心面で1度屈折するように作図します。
凸レンズの軸(光軸)に平行に入射した光がレンズで屈折して1カ所に集まる点を焦点(英語でfocusより、Fと書くことが多い)といいます。
レンズの中心から焦点までの距離を焦点距離といいます。
点とみなせる光源から四方に出る光のうち、凸レンズに入射する光の進み方は、以下の4つです。
①光軸に平行に進む光線は焦点を通る(解答例の上の光線)
②レンズの中心を通る光線はそのまま直進(解答例の中央の光線)
③焦点を通った光線は光軸に平行に進む(解答例の下の光線)
④それ以外の光線は、レンズまで直進し、レンズで屈折後、光の集合点に向かう。
像の作図は、①〜③のうちの2本を作図することでできます。
問2
解答:実像
解説:
凸レンズを通った光が集まってできる像を、実像といいます。
実像はスクリーン上に写すことができます。
物体を凸レンズの焦点(X1)の外側に置くと、物体から出た光が凸レンズで屈折し、集まって実像ができます。
このときに見える像は、スクリーン側から見ると、物体とは上下・左右が逆向きに見えるため、倒立実像といいます。
物体側から見た場合は、上下のみが逆の像が見えます。
問3
解答:A
解説:
光源とレンズ間の距離をa、焦点距離をfとおくと、
①a>2f(焦点距離の2倍):実物より小さい倒立実像
②a=2f:実物と同じ大きさの倒立実像
③f<a<2f:実物より大きい倒立実像。a=1.5fのとき、倒立実像の大きさは実物の2倍
④a=f:像ができない
⑤a<f(焦点の内側):実物より大きい正立虚像
光が集まらない像を虚像といい、スクリーンに映すことが出来ません。
物体を凸レンズの焦点の内側に置くと、凸レンズで屈折した光が目に入り、凸レンズを通して物体より大きな虚像が見えます(虫めがねの原理)。
このとき見える虚像は物体と同じ向きなので、正立虚像といいます。
図の凸レンズの焦点距離は、OX1間の4マスで、光源であるろうそくの先端PがBの位置にあるとき、OB間が8マスと焦点距離の2倍の位置にあるので、できる倒立実像の大きさは実物と同じ大きさの2マスです。
ろうそくの先端Pが焦点距離の2倍より外側にあるとき、できる倒立実像の大きさが実物より小さくなるので、答えはAとなります。
ろうそくの先端PがCの位置にあるとき、OC間が6マスと焦点距離の1.5倍の位置にあるので、できる倒立実像の大きさは、実物の大きさの1.5倍の3マスになります。
大問7
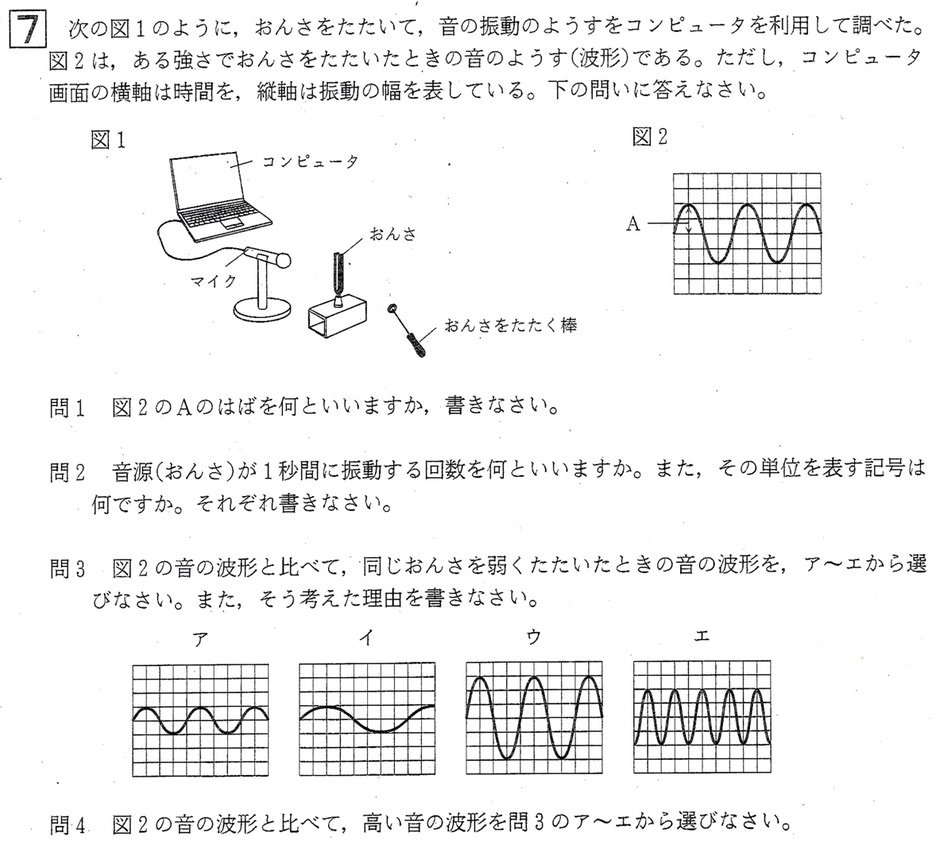
問1
解答:振幅
解説:
おんさやモノコードの弦などを音源といいます。
おんさを叩いたり、モノコードを弾くなどすると、音源が振動し、その振動が波として広がり、空気などの音を伝える物質(媒質)に次々と伝わることで、音が伝わります。
このようにして広がる音の波を音波といいます。
音源が1回振動すると、音源のまわりの空気が押されたり引かれたりして密度が変化し、1組の山と谷ができます。
コンピューターを用いて波形を調べると、図2のような波形になります。
このとき、図2の中央を横切る線であるベースラインから、山または谷までの幅を振幅といいます。
振幅が大きいほど音が大きく、振幅が小さいほど音が小さいです。
また、音波の波形の1つの山からとなりの山(1つの谷からとなりの谷)までが1つの波で、その長さを波長といいます。
図2の音波の波形は、左から右に、340m/sの速さで動いています。
1つの波が通過すると1回振動したといいます。
振動数とは、1秒間あたりに通過する波の数で、単位はHz(ヘルツ)です。
振動数が多いほど音が高く、振動数が小さいほど音が低いです。
問2
解答: 回数:振動数、単位:Hz
解説:
音源(おんさ)が1秒間に振動する回数とは、1秒間に通過した波の数という意味なので、これを振動数といいます。
振動数の単位は、Hz(ヘルツ)です。
例えば、図2の横の1目盛りが0.005秒のとき、1つの波の間隔は0.005秒×4=0.02秒より、0.02秒[s]で1回振動している(0.02秒で1つの波が通過している)ことから、
1秒間あたりに通過する波の数である振動数は、1/0.02s=100/2Hz=50Hz
となります。
問3
解答: 波形:ア、理由:振動数が同じで、振幅が小さいから。
解説:
同じ材質のおんさを弱く叩くと、振動数は変わりませんが振幅は小さくなるので、波形はアとなります(音が小さくなるだけ)。
同じ材質のおんさを強く叩くと、振動数は変わりませんが振幅は大きくなるので、波形はウとなります(音が大きくなるだけ)。
図1より振動数が多いおんさを同じ強さで叩くと、振動数が多くなり振幅は変わらないので、波形はエとなります(音が高くなるだけ)(ギュッと詰まった波になる)。
図1より振動数が少ないおんさを弱く叩くと、振動数が少なくなり振幅も小さくなるので、波形はイとなります(音が小さく低くなる)。
問4
解答:エ
解説:
問3解説参照。
大問8
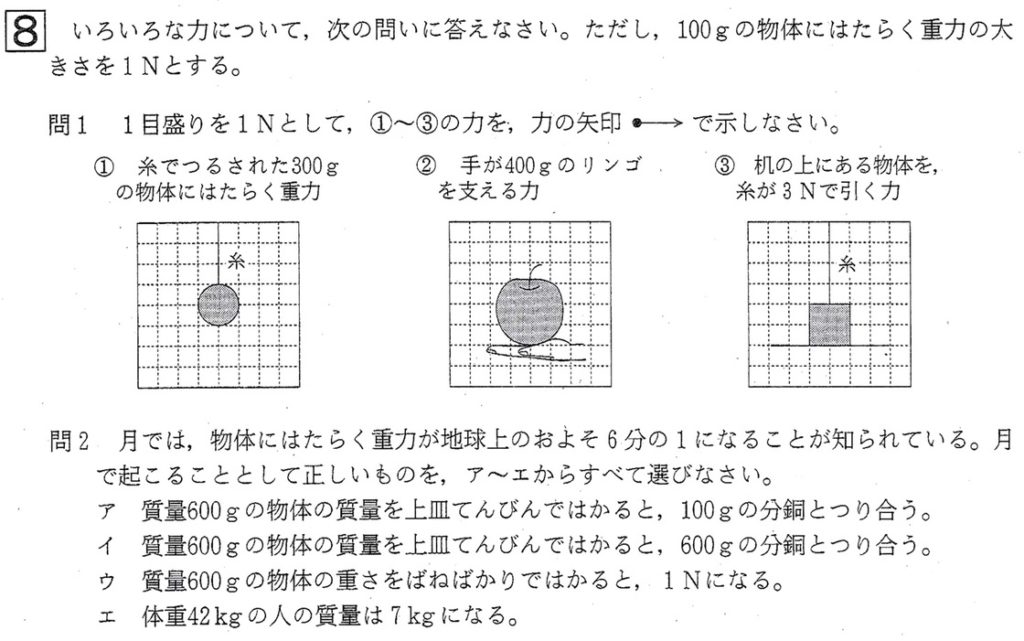
問1
解答:
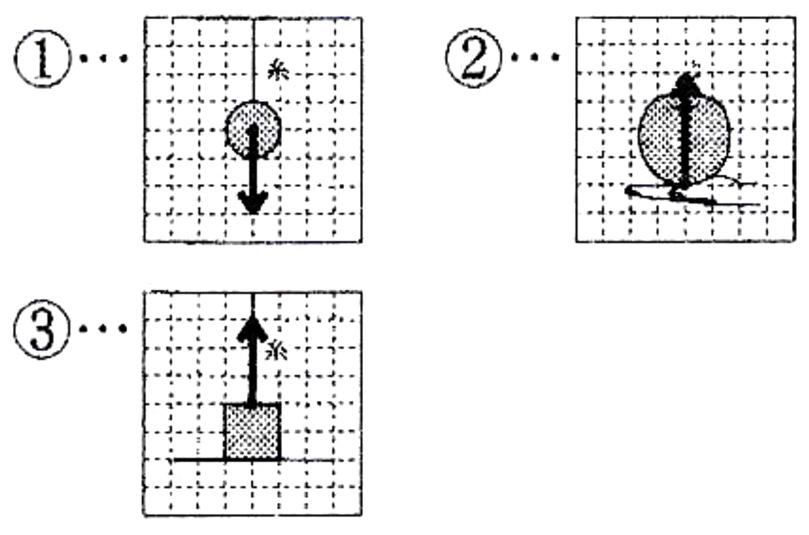
解説:
力は矢印で表します。
このとき、力の三要素である力の大きさを矢印の長さで、力の向きを矢印の指す向きで、力が加わる点である作用点を矢印の視点として、それぞれ表します。
力の矢印がのっている直線を、作用線といいます。
なお、地球上で質量100gの物体に働く重力(作用点は物体の中心)の大きさを1N(ニュートン)とすることが多いですが、
正確には、地球上で質量100gの物体に働く重力の大きさは0.98Nです。
①
問われているのは、「物体にはたらく重力」なので、力は物体の中心から(鉛直)下向きに働きます。
問題文で、「100gの物体に働く重力の大きさを1Nとする」とあり、①の物体の質量は300gより、重力の大きさは、1N/100g×300g=1N×3=3Nです。
よって、力の大きさである矢印の長さは3目盛り、力の向きは鉛直下向き、作用点は物体の中心となります。
もし「物体にはたらく力」と問われたら、物体には重力と、糸が物体を引く力の2つが働きます。
糸が物体を引く力の、力の大きさである矢印の長さは3目盛り、力の向きは鉛直上向き、作用点は物体と糸の接点となります。
物体は静止しているので、重力と、糸が物体を引く力は釣り合っていることになります。
もし「糸に働く力」と問われたら、糸には、物体が糸を引く力と、(図には無いが)手が糸を引く力の2つが働き、釣り合います。
物体と糸の接点では、物体が糸を引く力(作用する)と糸が物体を引く力(反作用する)の2つが発生します。
作用・反作用は同じ作用線上にあり、大きさが同じく向きが反対ですが、力が働く相手が異なるため、作用と反作用の2つの力は釣り合いとは無関係です。
②
問われているのは「手がリンゴを支える力」なので、手がリンゴに及ぼす力を調べます。
リンゴには4Nの重力が働き、リンゴと手との接点で、リンゴは手に4Nの力を及ぼします。
これを手がリンゴを4Nの力で及ぼし返すことで、リンゴは静止します。
ゆえに、リンゴと手との接点で、手がリンゴを支える力の、力の大きさである矢印の長さは4目盛り、力の向きは鉛直上向き、作用点はリンゴと手の接点、作用線はリンゴの中央を通る線となります。
③
問われているのは「糸が物体を引く力」なので、糸が物体に及ぼす力を調べます。
物体には3Nの重力が働き、糸と物体との接点で、物体は糸を3Nの力で鉛直下向きに力を及ぼします。
これを糸が3Nの力で及ぼし返すことで、物体は静止します。
ゆえに、糸と物体との接点で、糸が物体を引く力の、力の大きさである矢印の長さは3目盛り、力の向きは鉛直上向き、作用点は糸と物体の接点、作用線は物体の中央を通る線となります。
問2
解答:イ、ウ
解説:
質量600gの物体を、力の大きさを調べる実験器具であるばねばかりと、質量を調べる実験器具である上皿てんびんではかると、
地球上では物体に6Nの重力が、月では物体に1Nの重力が働くので、ばねばかりの値は、地球上では6N、月では1Nを示します。
上皿てんびんでは分銅を使用しますが、分銅にかかる100gあたりの重力の大きさは、地球上と月とで同じなので、
質量は地球上で600gなら、月面上でも600gになります。
大問9
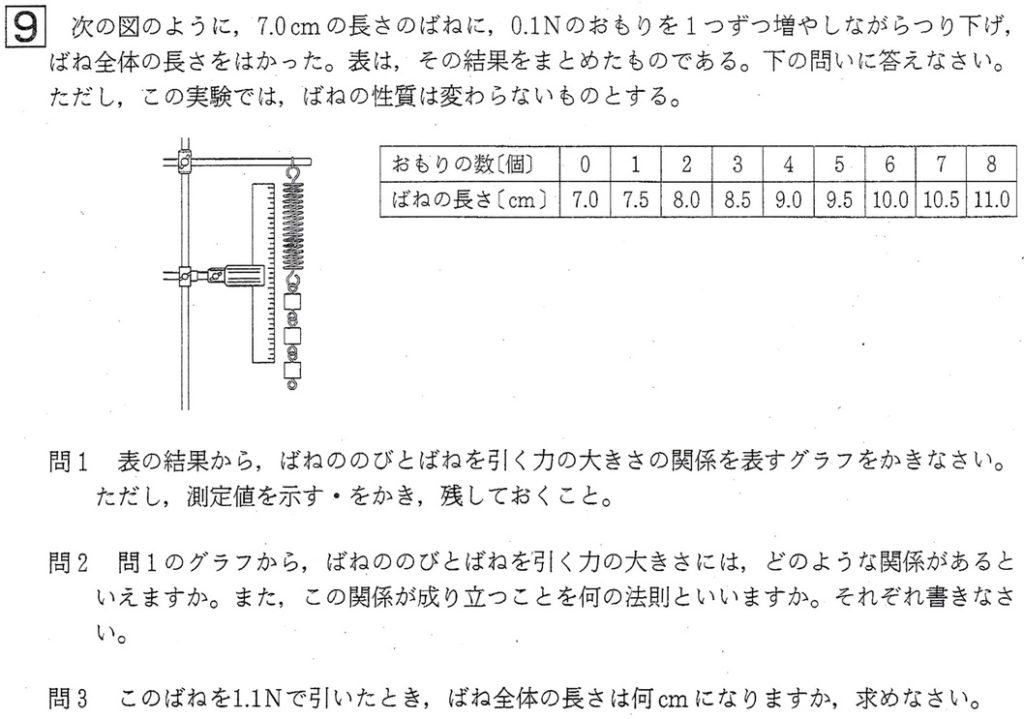
問1
解答:
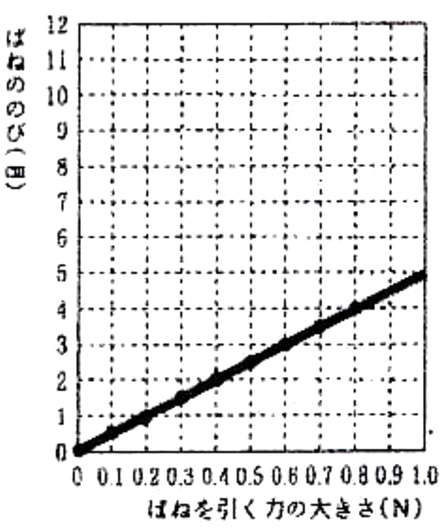
解説:
変形した物体がもとの形に戻ろうとする力を弾性力といいます。
ばねは伸びたり縮んだりすると、自然長(元の長さ)に戻ろうとする力が働き、これをばねの弾性力といいます。
ばねにつるすおもりの質量を2倍、3倍・・・にすると、ばねの伸びも2倍、3倍・・・になり、ばねの弾性力も2倍、3倍・・・になります(伸びた分だけ弾性力が増していく)。
バネの伸び縮みした長さと、ばねの弾性力=ばねにかかる力の大きさは比例関係にあり、これをフックの法則といいます。
実際に表の値をグラフ化する(これをプロットするという)と、ばねを引く力の大きさが増すに従い、ばねの伸びは直線的に増加している、すなわち比例関係にあることが分かります。
このグラフの傾きをばね定数[N/m]といい、単位よりばね定数は、ばねを1m伸ばしたり縮めたりするのに必要な力の大きさとなります。
問2
解答: 関係:比例、法則:フック(の法則)
解説:
問1解説参照。
問3
解答:12.5cm
解説:
表より、0.1Nのおもりを1つ増やすと、ばねは0.5cm伸びるので、ばね定数[N/m]の単位の見方に基づいて、ばねに1Nの力が加わったときのばねの伸びは、0.5cm/0.1N=5cm/Nとなります。
ゆえに、このばねを1.1Nの力で引いたとき、すなわち、このばねに1.1Nの力が加わったとき、ばねの伸びは、5cm/N×1.1N=5.5cmとなります。
ばね全体の長さは、自然長とばねの伸びとの和です。
自然長はばねに力が加わっていないときのばねの長さなので、表より、このばねの自然長は7.0cmです。
ゆえに、ばね全体の長さは、7.0cm+5.5cm=12.5cmとなります。
大問10

問1
解答: ①:0.06m2、②:12N、③:200Pa
解説:
①
単位に注意して解くだけです。
A面の面積[m2]=30cm×20cm=30/100m×20/100m=3/10×2/10m2=6/100m2=0.06m2
②
レンガの重さは、レンガにかかる重力の大きさのことです。
問題文に「レンガの質量を1.2kgとし、100gの物体に働く重力の大きさを1Nとする」とあるので、レンガにかかる重力の大きさは
1.2kg×1N/100g=1.2×1000g×1N/100g=1.2×10N=12N
③
ふれあう面の単位面積[m2]あたりに加わる垂直方向の力[N]を圧力といいます。
これから、圧力の単位は[N/m2]=[Pa]です。
圧力の単位に留意して解くと、A面の面積0.06m2が、レンガの重さが12Nより、
レンガのA面がスポンジに加える圧力[N/m2]の大きさは、
圧力[N/m2]=圧力[Pa]=12N/0.06m2=12×100/6N/m2=2×100N/m2=200N/m2=200Pa
問2
解答:A(面<)C(面<)B
解説:
圧力の単位[N/m2]に留意して以下のような比例式を立てます。
圧力A:圧力B=12N/30cm×20cm:12N/10cm×20cm=1/30×20:1/10×20=10×20:30×20=10:30=1:3
圧力B:圧力C==12N/10cm×20cm:12N/10cm×30cm=1/10×20:1/10×30=10×30:10×20=30:20=3:2より、
圧力A:圧力B:圧力C=1:3:2となり、圧力A<圧力C<圧力Bとなります。
ここで、レンガのA面、B面、C面をそれぞれ下にしてスポンジの上に置いたとき、いずれもスポンジに加える力[N]の大きさは12Nです。
レンガのA面、B面、C面の面積比は、
A面:B面:C面=30cm×20cm:10cm×20cm:10cm×30cm=6:2:3より、
B面<C面<A面となります。
これから、面が受ける垂直方向の力が同じ場合、
圧力比と面積比は逆比(大きさが逆になる)という関係が成り立ちます。
問3
解答:(大)気圧
解説:
空気の成分比率は、体積の割合で多い順から
窒素(約78%)、酸素(約21%)、アルゴン(約0.9%)、二酸化炭素(約0.04%)です。
このほか、ネオン、ヘリウムなども微量ですが含まれています。
これら空気を構成する原子や分子は質量[g]を持つので、力[N]を及ぼします。
地表面をおおう空気の層を大気、大気による圧力を気圧(大気圧)といいます。
空気の密度は、約1g/1000cm3です。
ここで、1辺10cmの立方体の空気のかたまりを考えると、体積が10cm×10cm×10cm=1000cm3より、この空気のかたまりの質量は
1g/1000cm3×1000cm3=1gとなります。
1gは、1円玉1枚の質量に相当します。
この空気のかたまりを床に置いたとき、ふれあう面の面積は10cm×10cm=10/100m×10/100m=1/10×1/10m2=1/100m2、床をおす力(重力の大きさ)は1N/100g×1g=1/100Nより、床が受ける圧力は
1/100N÷1/100m2=1N/m2=1Pa、となります。
これは高さ10cmあたりの圧力なので、1Pa/10cmとすることができます。
地表付近の気圧(1気圧)は、1013hPa=101300Paより、大気の厚さは
101300Pa÷1Pa/10cm=1013000cm=10130m=10130/1000km=10.13kmとなります。
しかし、実際の大気の厚さは約500kmです。
この差は、大気の厚さの計算過程で、空気の密度を、約1g/1000cm3としたためです。
しかし密度とは粒子の詰まり具合を表します。空気は上空に行くほど膨張し体積[cm3]が増加するため、密度[g/cm3]が減少します。
密度が減少すると、1辺10cmの立方体の空気のかたまりの質量[g]が減少し、床をおす力[N]も減少し、圧力(大気圧)[N/m2]も減少します。
これから、地表付近の気圧(1気圧)を1013hPa=101300Paとするためには、大気の厚さを厚くして、質量を増やす必要があるため、実際の大気の厚さは理論値10.13kmより遙かに大きい約500kmとなります。
大問11
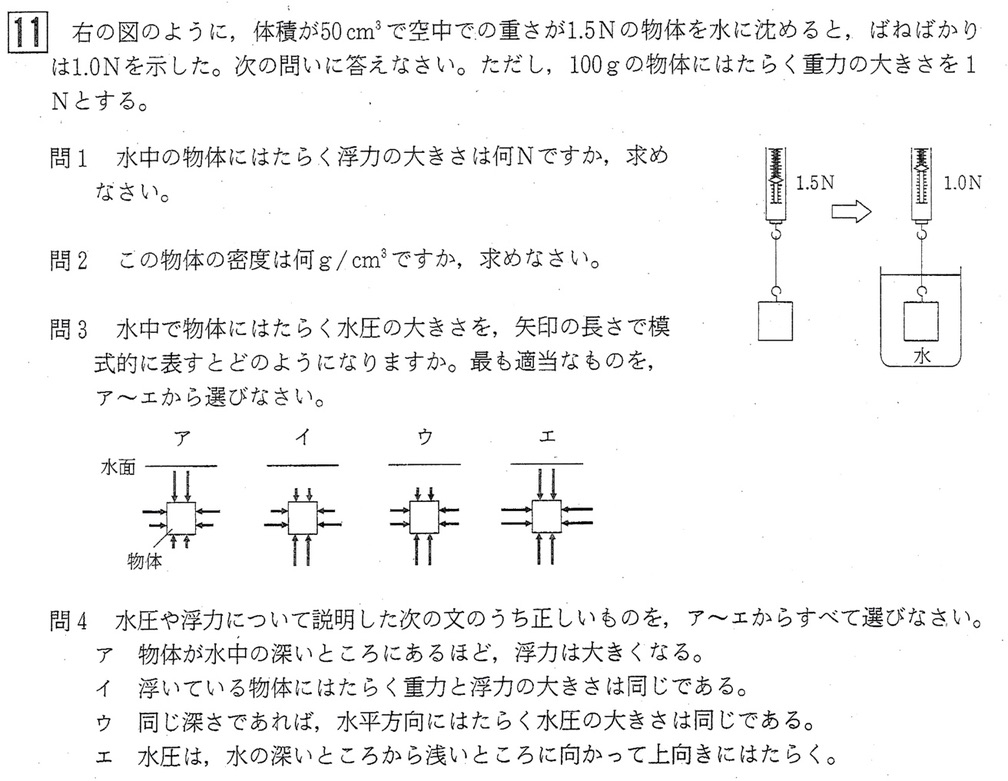
問1
解答:0.5N
解説:
ばねばかりを用いて、物体の重さを水中ではかると、物体は水から鉛直上向きの力を受け、空気中ではかるよりも軽くなる。
この力を浮力といいます。
物体は水中では、上面と下面、左右の面それぞれから水の圧力である水圧を受けます。
左右の面が受ける水圧の大きさは等しいので、互いに打ち消し合います。
しかし、上面と下面では、下面にかかる水圧の大きさ(鉛直上向き)が上面にかかる水圧の大きさ(鉛直下向き)より大きいため、その差が浮力となります。
また、浮力[N]とは物体が押しのけた流体の重さ[N]ということができ、これをアルキメデスの原理といいます。
仮に、水の密度を1.0g/cm3(4℃の水)とします。
物体の体積は50cm3より、物体をこの水に完全に沈めた場合、物体が押しのけた水の体積は50cm3、50cm3の水の質量[g]は、1.0g/cm3×50cm3=50gです。
100gの物体にはたらく重力の大きさを1Nと仮定すると、50cm3の水の重さ[N]は、1N/100g×50g=1/2N=0.5Nとなるので、
物体に働く浮力の大きさは0.5Nとなります。
問2
解答:3g/cm3
解説:
密度の単位[g/cm3]に注意して解きます。
問題文より、この物体の体積は50cm3です。
この物体の空中での重さ、すなわち物体に働く重力の大きさは1.5Nで、100gの物体にはたらく重力の大きさを1Nとしているので、この物体の質量は、
1.5N÷1N/100g=1.5×100g=150gです。
これより、密度の単位[g/cm3]に合わせて密度を求めると、
密度[g/cm3]=150g/50cm3=3.0g/cm3
※問題文に「1.5N」「1.0N」と書かれているので、少数第一位まで答えます。
問3
解答:イ
解説:
問1解説参照。
左右の面が受ける水圧の大きさは、深く沈むほど大きくなることに注意してください。
問4
解答:イ、ウ
解説:
・ア
アルキメデスの原理より、物体に働く浮力の大きさは、物体の体積に依存します。
ゆえに、物体が水中に完全に沈むと、物体に働く浮力の大きさはそれ以上増加しません。
・イ
正しい。
水に浮いている物体にかかる重力の大きさと浮力の大きさが釣り合うため、水は液体に浮きます。
・ウ
正しい。問3解説参照。
・エ
これは浮力の説明です。
物体は水中では、上面と下面、左右の面それぞれから水の圧力である水圧を受けます。
左右の面が受ける水圧の大きさは等しいので、互いに打ち消し合います。
しかし、上面と下面では、下面にかかる水圧の大きさ(鉛直上向き)が上面にかかる水圧の大きさ(鉛直下向き)より大きいため、その差が浮力となります。