こんにちは、個別指導塾まさです。
今回は、中2理科3学期定期テスト（学年末テスト）過去問の解説第2弾です。
実際に定期テストで出題された問題の中で、とくに差が付く問題を厳選して解説します。
オンライン個別指導塾と家庭教師をやっています。北大院卒、指導経験20年以上。当塾は中上位高校志望の子が多いですが、勉強が苦手な子も多数在籍しています。今の学力は不問ですので、気軽にお申し込みください。授業料は1回70分 3,000円〜です。
＞＞教師紹介・料金・授業内容
＞＞体験授業かんたんお申し込み
＞＞お問い合わせ
第1問
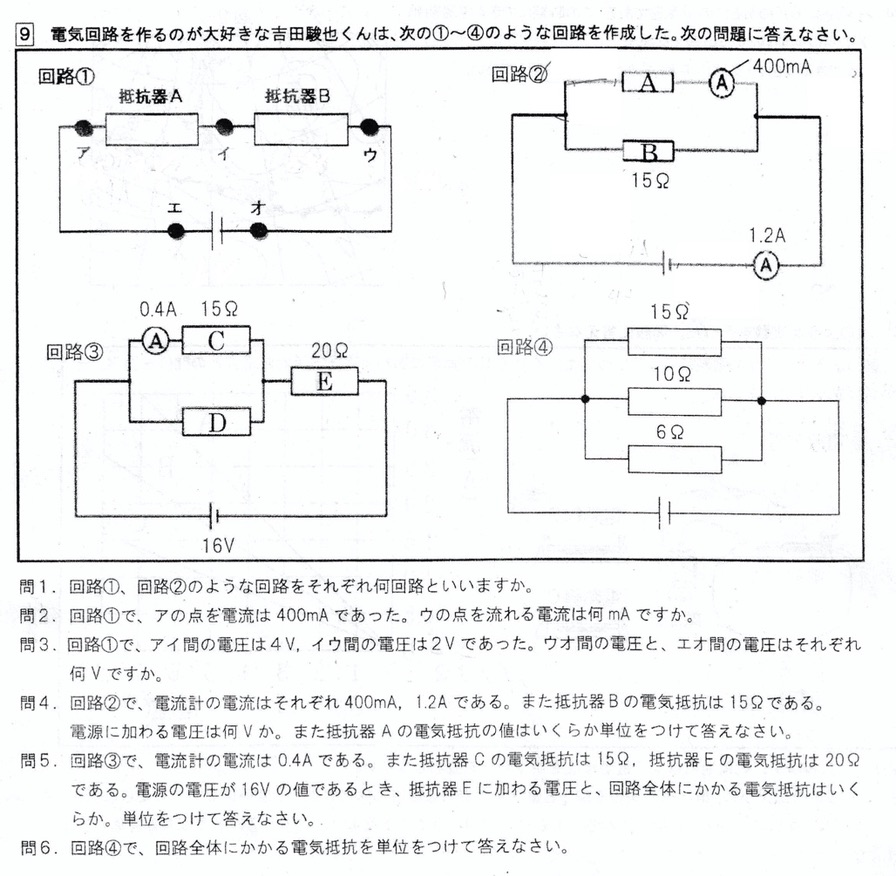
（1）
回路①は直列回路、回路②は並列回路です。
（2）
直列回路より、各抵抗に流れる電流の大きさは同じです（400mA）。
（3）
電圧は電流を流す力で、抵抗や電源に加わります。
よって、ウオ間の電圧は0Vです。
直列回路では、電源の電圧＝各抵抗の部分電圧の和、となるので、エオ間の電圧は2V＋4V＝6Vです。
（4）
抵抗器Bに流れる電流の大きさは、並列回路より、1.2A – 0.4A＝0.8A。
オームの法則より、抵抗器Bに加わる電圧の大きさは、
V=IR＝0.8A×15Ω＝8×15/10＝120/10＝12V
並列回路では、電源の電圧＝各抵抗に加わる電圧大きさ、となるので、電源に加わる電圧の大きさは12Vです。
抵抗器Bに流れる電流の大きさは0.4A、加わる電圧の大きさは12Vなので、オームの法則より、
V=IR ⇔ R=V/I＝12V/0.4A＝120/4＝30Ω
（5）＜難＞
抵抗器Cに着目して、オームの法則より、抵抗器Cに加わる電圧の大きさは、
V=IR＝0.4A×15Ω＝4×15/10＝60/10＝6V
これより、抵抗器Eに加わる電圧の大きさは、16V – 6V＝10V
抵抗器Eに流れる電流の大きさは、オームの法則より、
V=IR ⇔ I=V/R＝10V/20Ω＝1/2＝0.5A
電源の電圧が16Vなので、回路全体の抵抗の大きさは、オームの法則より、
V=IR ⇔ R=V/I＝16V/0.5A＝16×2＝32Ω
（6）
15Ωの抵抗と10Ωの抵抗の合成抵抗は、
(15×10)/(15+10)＝150/25＝6Ω
6Ωの合成抵抗と、6Ωの合成抵抗は、抵抗値が同じなので、
6/2Ω＝3Ω
第2問
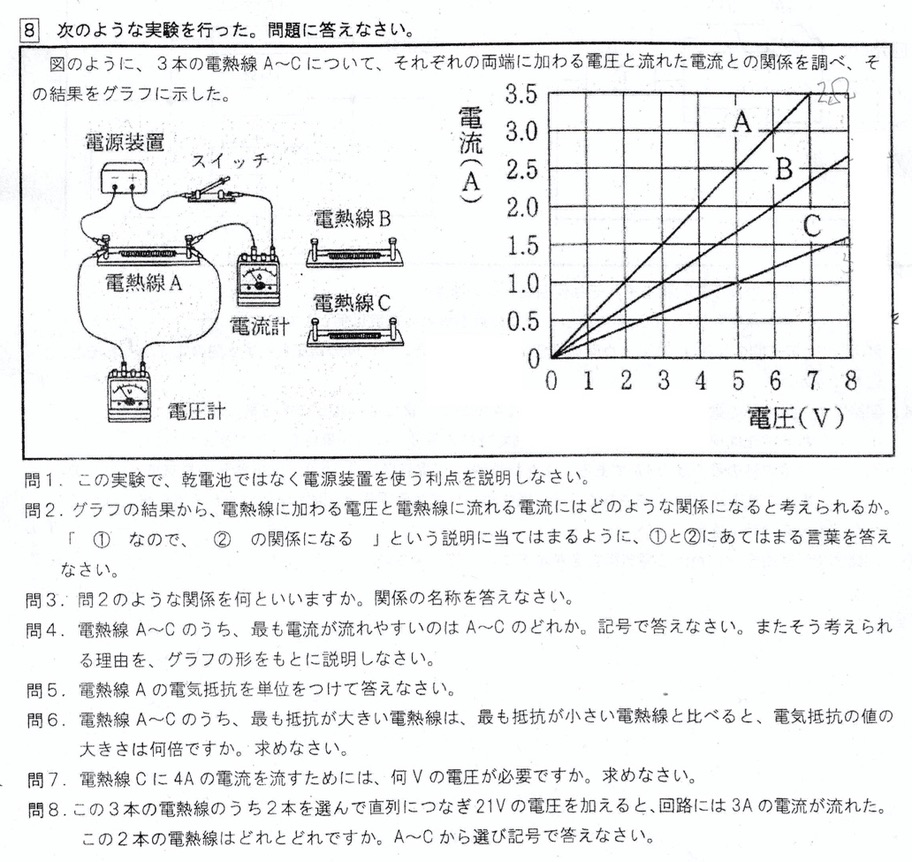
（1）
電源装置の利点は、電圧を自由に調節できることです。
これより、各抵抗の電圧を変えたときに流れる電流の大きさが測定でき、抵抗の抵抗値をオームの法則から計算することができます。
また、電源装置は乾電池とは違い、電圧が下がらないことも利点の1つです。
（2）
オームの法則より、
V=IR ⇔ I=1/R×V
これより、電熱線を流れる電流の大きさは加わる電圧の大きさに比例し、比例定数は1/Rです。
グラフは原点を通る直線となります。
（3）
答：オームの法則（解説略）
（4）
抵抗は電流の流れにくさなので、各電熱線に同じ電圧を加えたときに、流れる電流が大きいほど抵抗が小さくなります。
各電熱線に5Vの電圧を加えると、電熱線Aに流れる電流が2.5Aと最も大きくなるので、抵抗が最も小さく電流が最も流れやすいと言えます。
オームの法則より、V=IR ⇔ I=1/R×V、なので、傾き＝1/Rが大きいとき、電圧を変化させたときに、電流の大きさがより大きく変化することが分かります。
つまり、グラフの傾きが大きいほど、電流が流れやすい抵抗であると言えます。
（5）
グラフより、電熱線Aに5Vの電圧を加えると、電流の大きさが2.5Aとなるので、オームの法則より、
V=IR ⇔ R=V/I＝5V/2.5A＝50×25＝2Ω
（6）＜難＞
オームの法則より、
V=IR ⇔ R=V/I
これより、抵抗は電圧に比例し電流に反比例することから、電流の大きさが一定のとき、
抵抗の比＝電圧の比
が成り立ちます。
グラフより、各電熱線に1.0Aの電流が流れたときの電圧の比は、
電熱線A：電熱線B：電熱線C＝2：3：5
なので、電熱線Cの抵抗値は電熱線Aの5/2＝2.5倍となります。
（7）
（2）解説より、電熱線を流れる電流の大きさは電圧に比例します。
電熱線Cに1.0Aの電流が流れたとき、加わる電圧の大きさは5Vなので、4倍の4.0Aの電流が流れたとき、加わる電圧の大きさは5V×4＝20Vとなります。
（8）
回路全体の抵抗の大きさは、オームの法則より、
V=IR ⇔ R=V/I＝21V/3A＝7Ω
オームの法則を用いて電熱線A〜Cの抵抗の大きさを計算すると、
電熱線Aは2Ω、電熱線Bは3Ω、電熱線Cは5Ωなので、直列回路においては、電熱線AとCを組み合わせることで、題意を満たします。
並列回路の合成抵抗では、合成抵抗の大きさは各抵抗の大きさより小さくなるので、題意を満たす組み合わせは存在しません。
スポンサーリンク
第3問
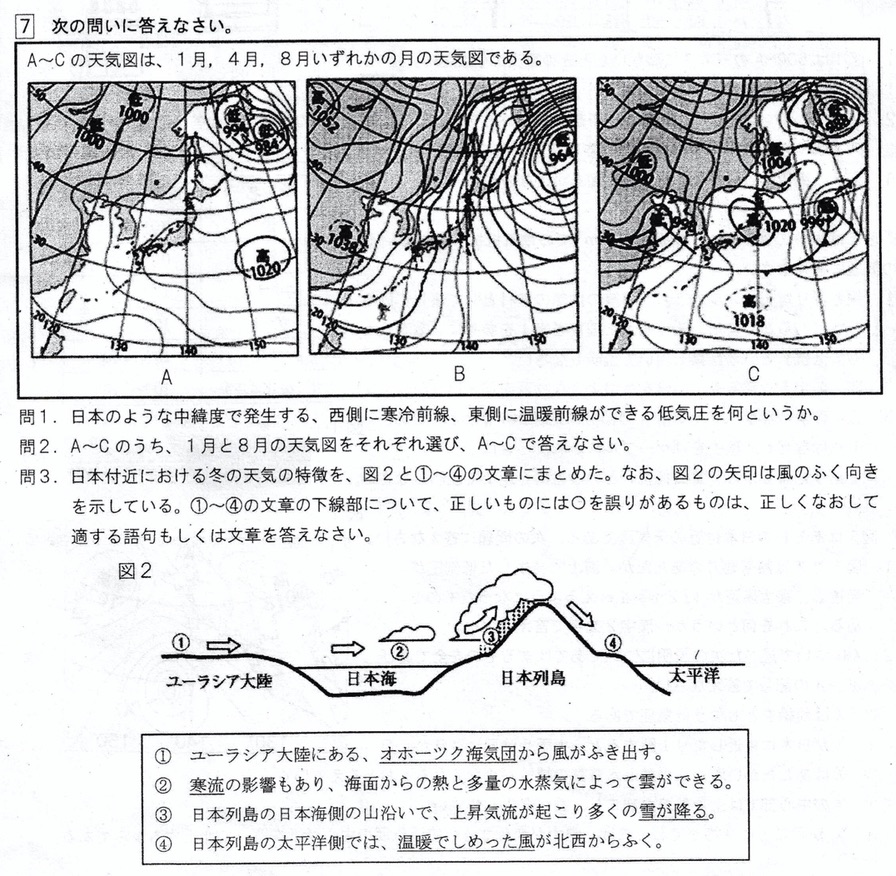
（1）
答：温帯低気圧（解説略）
（2）
冬は西高東低の気圧配置で、等圧線が縦縞となることから、Bが正解です。
夏は南高北低の気圧配置となるので、Aが正解です。
Cは移動性高気圧と温帯低気圧が偏西風によって交互に移動していることから、春か秋の気圧配置です。
（3）
①
冬に発達するユーラシア大陸の気団は、シベリア気団です。
②
冬の季節風はユーラシア大陸から吹くため、冷たく乾燥しています。
そのため冬の季節風は、日本海で水蒸気と熱を補給するため、湿度が非常に高くなります。
日本海を流れる海流は暖流です。
③
正しい。
雲は上昇気流によって生じます。
図はフェーン現象と同じ状況で、空気塊が山を上昇するので、山の風上側で雲が発生します。
水蒸気を含んだ空気が上昇すると、大気圧が低くなり、内圧が大気圧より大きくなります。
これより、空気が断熱膨張して温度が下がり露点以下になると、水蒸気が凝結して水滴に変わり雲ができます。
水滴は、空気中のちりやほこりが核の役目をして、他の水滴と衝突して大きくなります。
水滴の質量が小さいときは、上昇気流に支えられて落下しませんが、水滴が成長する落下し、雨や雪が降ります。
④
空気塊が下降すると、大気圧が大きくなり、空気が断熱圧縮されて温度が上がり、水滴が水蒸気となって空気中にもどることで、天気が良くなります（高気圧）。
空気塊は山の風上側で雪を降らせ、水分を放出したことで、乾燥した空気となります。
これが山の風下側で寒冷で乾いた風となり、太平洋側を流れます。
（4）
答：梅雨前線（解説略）
（5）
停滞前線は、小笠原気団とオホーツク海気団の勢力がほぼ釣り合ったときに出来る前線です。
第4問
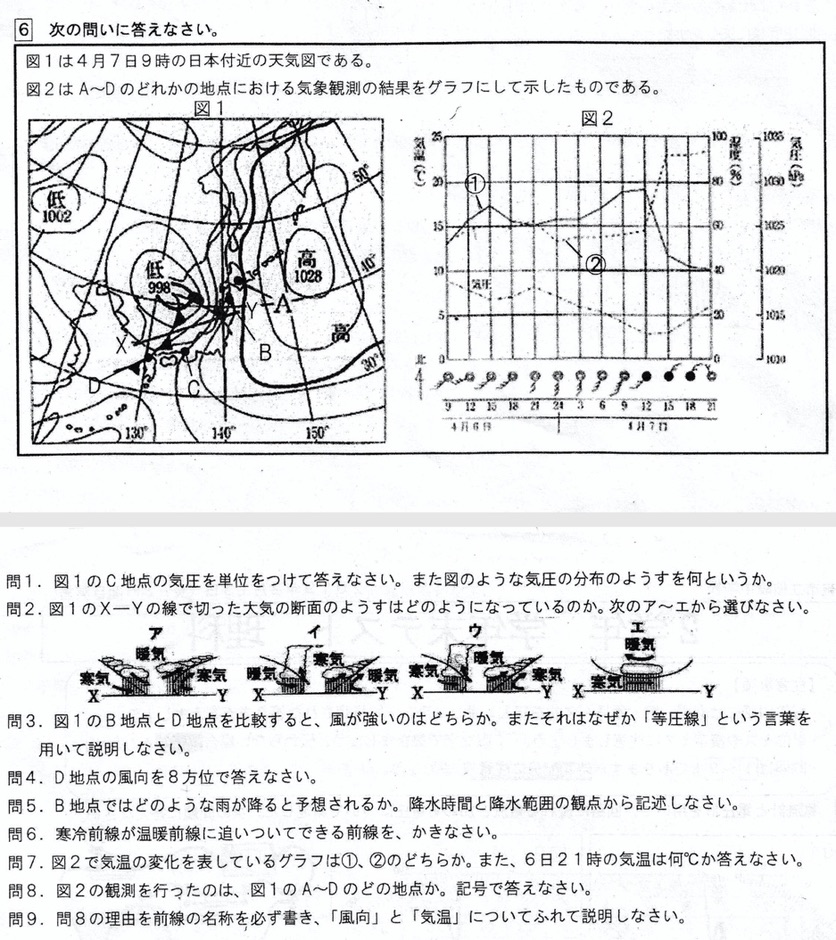
（1）
等圧線は低気圧の中心から4本目の位置にあるので、998＋4×4＝1012hPa
図のような気圧の分布のようすを、気圧配置といいます。
（2）
温帯低気圧の左側では、寒気が偏西風によって西から東へ進み、暖気と接して前線面が発生します。
前線面と地面との接点である寒冷前線では、寒気が垂直に押し上げて激しい上昇気流が生じるため、前線の左側で積乱雲や積雲が発生します。
積乱雲により、短時間に狭い範囲で非常に強い雨が降ります。
温帯低気圧の右側では、暖気が偏西風によって西から東へ進み、寒気と接して前線面が発生します。
前線面と地面との接点である温暖前線では、暖気が寒気の上にはい上がり、ゆるやかな上昇気流が生じるため、前線の右側で乱層雲−高層雲−巻層雲−巻雲が生じます。
乱層雲により、広範囲に長い時間弱い雨が降ります。
よって、正解はウです。
（3）
等圧線の間隔が狭いと、気圧傾度が大きくなり、風が強く吹きます。
これより、Bが正解です。
（4）
D地点は暖気にいると思われるので、南西の風が吹いています。
（5）
B地点では乱層雲に覆われているので、広範囲に長い時間弱い雨が降ります。
（6）
正解は閉塞前線です。
寒冷前線の寒気が温暖前線の寒気より温度が低いとき寒冷型閉塞前線に、
温暖前線の寒気が寒冷前線の寒気より温度が低いとき温暖型閉塞前線に、
それぞれなります。
温帯低気圧は閉塞前線が発生後、消滅します。
（7）
4月7日の12時頃に、風向が南寄りから北寄りに急変していることから、寒冷前線が通過しています。
寒冷前線が通過すると寒気に覆われるため、気温が急降下します。
よって、正解は①です。
グラフより、6日21時の気温は15℃です。
（8）
（7）解説より、図2の観測地点はCです。
（9）
4月7日の12時頃に、風向が南寄りから北寄りに急変し、気温が急降下したことから、寒冷前線が通過していることが分かります。
