👉教師紹介・料金
※授業料1回1,500円+交通費(コミコミ最大3,000円)・入会金なし・お好きな日時に受講・3回のお試し期間あり(無料教材あり)
☆学力テストはこれで完璧!オリジナル教材☆
👉北海道学力テストはこれで完璧!オリジナル教材+過去問一覧
※過去問の販売はできませんのでご注意ください。
大問1
問1
解答:道管
解説:
植物細胞には葉緑体があり、光合成は葉緑体で行われます。
根で吸収した水が茎の道管(維管束の内側)から葉の維管束である葉脈(維管束の上側)を通り葉緑体に届けられ、
孔辺細胞の隙間である気孔で吸収された二酸化炭素を日光(光エネルギー)を用いて、単糖類であるグルコース(ブドウ糖)と酸素に合成されます。
グルコースは水に溶けやすく、このままの形では葉に栄養分を貯蔵できないため、グルコースが多数つながった水に溶けにくいデンプンにつくり変えられます。
夜間に水に溶けやすい二糖類のスクロース(ショ糖)に変えられ、師管を通ってからだの各部へ運ばれて、呼吸や成長の材料として使われます。
問2
解答:蒸散
解説:
植物の葉の表、葉の裏、茎には気孔(孔辺細胞の隙間)があり、気孔から酸素や二酸化炭素が出入りし、水蒸気が出て行きます。
植物体内の水が、気孔から水蒸気となって体外に放出される現象を蒸散といいます。
蒸散量を調べる実験では、問題の通り、ワセリンがよく用いられます。
また、蒸散量を正確に調べるために、試験管に油を入れ、水が試験管から蒸発するのを防止します。
蒸散がもつ3つのはたらき(メリット)は、
①体内の水分量の調節
②植物体の温度調節
→蒸散が起こると気化熱により植物体の温度が下がる
③水分移動の促進
→葉で蒸散が起こると植物体の水分量が減り、葉の細胞内液の濃度が高くなり、根から道管に水を押し上げる力である根圧と、葉が道管から水を吸収しようとする力である吸水力により、水分移動が促進される
問3
解答:気孔
解説:
問2解説参照。
問4
解答:(多い)A→C→B(少ない)
解説:
気孔は孔辺細胞のすきまにできる小さな穴です。
多くの陸上植物は、葉の表側より裏側に気孔が多く分布しますが、オニユリなどでは葉の表と裏でほぼ同数の気孔が分布しています。
気孔は茎にもあることに注意してください。
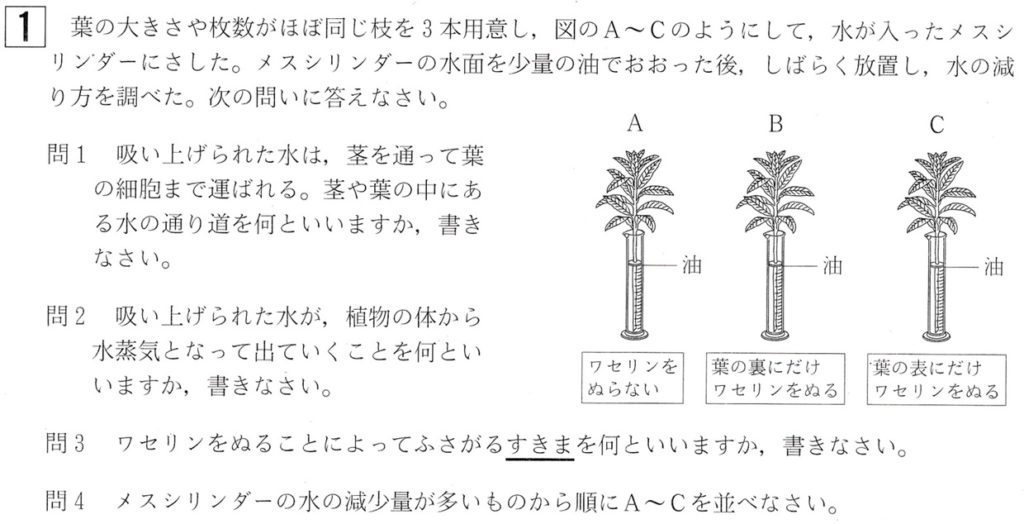
この問題では、「葉の大きさや枚数がほぼ同じ枝を3本用意し」とあるので、葉の表側と裏側からの1時間あたりの蒸散量は、A、B、Cすべて同じとみなしてよいです。
図のAでは、ワセリンをぬっていないので、葉の表側と葉の裏側と茎から蒸散が起こっています(1時間あたりの蒸散量をAと置きます)
図のBでは、葉の裏側にワセリンをぬっているので、葉の表側と茎から蒸散が起こっています(1時間あたりの蒸散量をBと置きます)
図のCでは、葉の表側にワセリンをぬっているので、葉の裏側と茎から蒸散が起こっています(1時間あたりの蒸散量をCと置きます)
この問題では、葉の裏側に気孔が多く分布するという仮定をしないと解答できないので、採取した植物は、葉の裏側に気孔が多く分布しているということにします。
すると、1時間あたりの蒸散量は、A>C>B、ということになり、解答のとおりとなります。
大問2
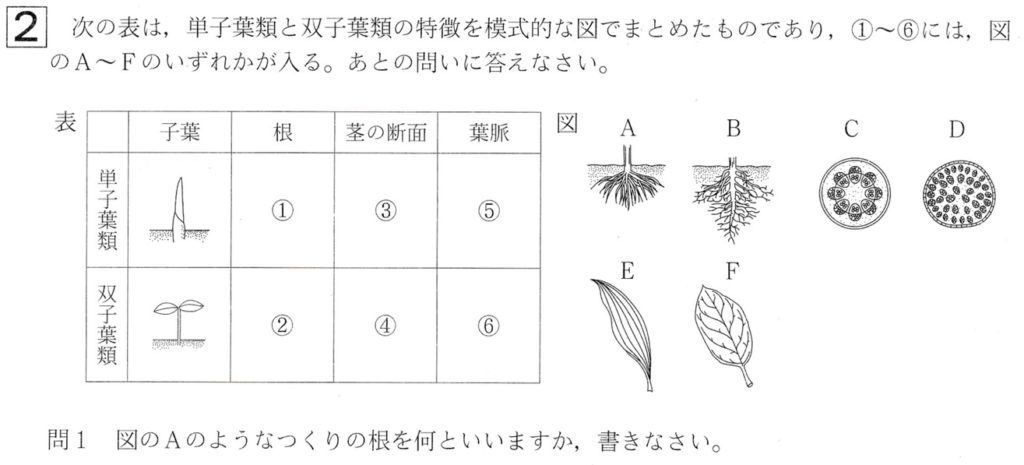

問1
解答:ひげ根
解説:
植物の分類の観点はまず、種子をつくるか否かで大別します。
種子を作る植物を種子植物といいます。
種子植物はさらに、胚珠が子房に包まれているか否かで分類し、胚珠が子房に包まれている植物を被子植物、胚珠がむきだしの植物を裸子植物といいます。
被子植物はさらに、子葉の枚数で分類し、子葉が1枚の植物を単子葉類、子葉が2枚の植物を双子葉類といいます。
双子葉類は、子葉が2枚、葉脈(葉の維管束)が網状脈(F)、茎の維管束が輪状に並びます(C)。
維管束とは、道管と師管の束のことです。
道管は、根から吸収された水や肥料分が通る管で、茎では維管束の内側にあります。
師管は、葉で光合成で作られた養分(デンプン→ショ糖)が通る管で、茎では維管束の外側にあります。
双子葉類の根は、主根と側根からなり(B)、根の先端ちかくに根毛があり、表面積を広げる構造をしており、これにより水や肥料分を効率よく吸収できます。
単子葉類は、子葉が1枚、葉脈(葉の維管束)が平行脈(E)、茎の維管束が全体に散らばっています(D)。
双子葉類と同じく、道管は維管束の内側に、師管は維管束の外側にあります。
単子葉類の根はひげ根で(A)、根の先端ちかくに根毛があり、表面積を広げる構造をしており、これにより水や肥料分を効率よく吸収できます。
双子葉類はさらに、花弁がくっついているか否かで分類し、花弁がくっついている植物を合弁花類(ツツジ)、花弁が離れている植物を離弁花類(アブラナ)といいます。
単子葉類として、イネ・トウモロコシ・スズメノカタビラ・ユリ・アヤメ・ツユクサ・チューリップを、
合弁花類として、ツツジ・タンポポ・アサガオを、
離弁花類として、サクラ・アブラナ・エンドウを、
裸子植物として、マツ、スギ、ヒノキ、イチョウ、ソテツを
それぞれ覚えましょう。
これに加えて、ホウセンカは双子葉類であることも覚えましょう。
種子を作らず、胞子で増える植物(H)は、今度は維管束があるかどうか、または、根・茎・葉の区別かあるかどうかで大別され、
維管束がある植物をシダ植物(IとD)、ない植物をコケ植物(E)といいます。
シダ植物として、イヌワラビ・ゼンマイ・スギナを、
コケ植物として、スギゴケ・ゼニゴケを、
それぞれ覚えましょう。
問2
解答:ウ
解説:
問1解説参照。
問3
解答:c、e
解説:
単子葉類として、イネ・トウモロコシ・スズメノカタビラ・ユリ・アヤメ・ツユクサ・チューリップを、
合弁花類として、ツツジ・タンポポ・アサガオを、
離弁花類として、サクラ・アブラナ・エンドウを、
裸子植物として、マツ、スギ、ヒノキ、イチョウ、ソテツを
シダ植物として、イヌワラビ・ゼンマイ・スギナを、
コケ植物として、スギゴケ・ゼニゴケを、
それぞれ覚えましょう。
問4
解答: なかま:被子植物、特徴:胚珠が子房の中にある
解説:
種子を作る植物を種子植物といいます。
種子植物はさらに、胚珠が子房に包まれているか否かで分類し、胚珠が子房に包まれている植物を被子植物、胚珠がむきだしの植物を裸子植物といいます。
被子植物はさらに、子葉の枚数で分類し、子葉が1枚の植物を単子葉類、子葉が2枚の植物を双子葉類といいます。
被子植物であるアブラナを例にとって考えます。
花の4要素は、外側から、がく・花弁・おしべ・めしべの順です。
おしべのやくにの中には花粉母細胞(核相2n)があり、そこから成熟花粉(核相n、生殖細胞(精細胞)なので減数分裂して染色体の数が半分になっている)が作られます。
花粉がめしべの柱頭に付着することが受粉で、受粉後、花粉管の伸張により精細胞が胚珠の中の卵細胞(核相n)と受精し受精卵となります。
受精後、胚珠は種子に、子房は果実に、受精卵は胚となります。
なお、生殖細胞の呼び方は、被子植物の場合は精細胞と卵細胞、動物の場合は精子と卵です。
大問3
問1
解答:融点
解説:
固体から液体への状態変化を融解、
液体から固体への状態変化を凝固、
液体から気体への状態変化を気化、
気体から液体への状態変化を液化、
固体から気体または気体から固体への状態変化を昇華といいます。
物質が融解し始めるときの温度を融点、
凝固し始めるときの温度を凝固点、
気化し始めるときの温度を沸点といいます。
天気の分野において、水蒸気が液化し始めるときの温度を露点といいます。
純粋な物質の融点と沸点は決まっており、また融点と凝固点は一致します。
問2
解答:イ
解説:
パルチミン酸の融点は62.7℃、沸点は360℃です。
パルチミン酸の温度が、
62.7℃より小さいなら固体の状態で、熱を加えると温度が上昇していきます。
62.7℃なら固体と液体が共存した状態で、熱を加えても固体を液体にするのに熱エネルギーが使われるため、温度は上昇しません。
62.7℃より大きく360℃より小さいなら液体の状態で、熱を加えると温度が上昇していきます。
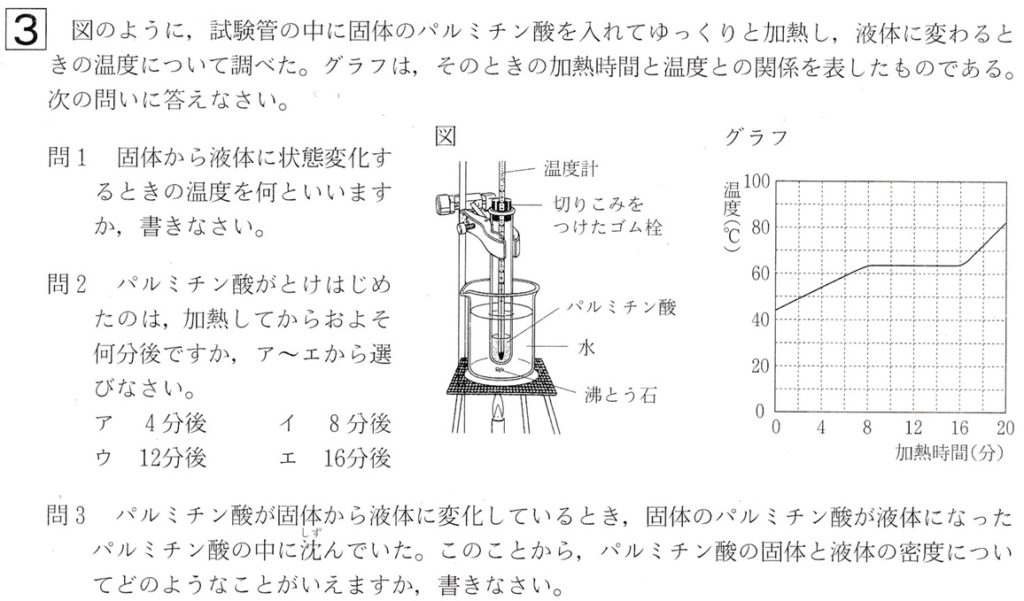
グラフを見ると、パルチミン酸の融点または凝固点が62.7℃らしく見えるので、用いたパルチミン酸は不純物が含まれていない純粋なパルチミン酸です。
よって、パルチミン酸が溶け出したのはおよそ8分後、固体のパルチミン酸が完全に液体になったのがおよそ16分後です。
加熱時間が0〜8分ではパルチミン酸は固体の状態、16分後以降は液体の状態です。
なお、パルチミン酸は水を通じて加熱されていますが、水の沸点は100℃なので、加熱を続けてもパルチミン酸の温度は100℃より上昇せず、パルチミン酸の沸点360℃を超えないため、液体の状態のままです。
パルチミン酸とは、バターやパーム油などに含まれる白色の血漿で、ろうそくの材料の1つとしても用いられています。
問3
解答:パルチミン酸の固体の密度は、液体の密度より大きい
解説:
水以外の物質について、液体と固体において、
液体の密度が固体より小さい場合、密度が大きい固体は液中に沈みます。
液体の密度が固体より大きい場合、密度が小さい固体は浮きます。
液体の密度と固体の密度が等しい場合、固体は液体中で静止します。
水以外の物質において、物質を構成する粒子の動きは、
固体→粒子は集合して細かく振動。体積(cm3)が小さく質量(g)は他の状態と同じより、密度(g/cm3)は最も大きい。
液体→粒子どうしがくっついたり離れたりする。体積(cm3)が固体より大きく質量(g)は他の状態と同じより、密度(g/cm3)は固体の状態より小さい。
気体→粒子は激しく動き自由に飛び回る。体積(cm3)が液体より遙かに大きく質量(g)は他の状態と同じより、密度(g/cm3)は液体の状態よりかなり低い。
よって、固体の状態のパルチミン酸は、液体の状態のパルチミン酸より密度(g/cm3)が大きいので、沈みます。
大問4

問1
解答:飽和水溶液
解説:
溶質とは溶けるもの、溶媒とは溶かすもので、水は溶媒です。
溶解度とは、水100gに溶ける溶質の限界の質量です。
溶質が限界まで溶けている状態の水溶液を、飽和水溶液といいます。
問2
解答:D
解説:
「60℃の水100gにとけるだけとかしたとき」とあるので、60℃の溶解度をグラフより調べます。
物質Aの溶解度がおよそ110g、物質Bの溶解度がおよそ58g、物質Cの溶解度がおよそ38g、物質Dの溶解度がおよそ15gと、物質Dの溶解度が最も小さいです。
よって、60℃の水100gにとけるだけとかしたとき、とける量が最も少ない物質は、物質Dです。
問3
解答:A
解説:
再結晶の方法として、①水溶液を冷やして取り出す、②水溶液を蒸発させて取り出す、の2つがあります。
①水溶液を冷やして取り出す
温度を下げると溶解度が大きく変化する物質に用いられます(温度による溶解度の変化が大きい)。
溶解度曲線を見ると、物質A(硝酸カリウム)は温度を下げると溶解度が大きく変化するので、硝酸カリウムの再結晶には水溶液を冷やして取り出す方法が用いられます。
②水溶液を蒸発させて取り出す
温度を下げても溶解度があまり変化しない物質に用いられます(温度による溶解度の変化が小さい)。
溶解度曲線を見ると、物質C(塩化ナトリウム)は温度を下げても溶解度があまり変化しないので、塩化ナトリウムの再結晶には水溶液を蒸発させて取り出す方法が用いられます。
硝酸カリウムは温度による溶解度の変化が大きい、塩化ナトリウムは温度による溶解度の変化が小さいことは、溶解度曲線と合わせて覚えましょう。
硝酸カリウムの再結晶において、以下の2パターンの問題が出題されます。
①この温度ですべて溶けるか否か
→実験内容を溶解度曲線に合わせる。具体的には、実験で用いた水の質量を100gになるよう、水と溶媒の質量を等倍する。
②温度を下げたとき何gの結晶が析出するか
→溶解度曲線を実験内容に合わせる。具体的には、溶解度曲線の水の質量100gを、実験で用いている水の質量になるよう等倍する。
この問題では、60℃飽和水溶液を冷やして、析出する結晶の質量が最も多い物質が問われています。
具体的な質量の値ではなく、質量の大小関係が問われているので、「①この温度ですべて溶けるか否か」の方法で解きます。
グラフの横軸の60℃から、それぞれの物質の溶解度曲線に棒線を引き、20℃まで左にスライドさせると、棒線が溶解度曲線を越えた部分が析出する結晶の質量です。
物質Aはおよそ80g(110g-30g)、物質Bはおよそ48g(58g-10g)、物質Cはおよそ1g(38g-37g)、物質Dはおよそ7g(15g-8g)析出するので、
飽和水溶液の温度を60℃から20℃に下げると、物質Aの結晶が最も多く析出します。
問4
解答: 物質:C、方法:水を蒸発させる
解説:
問3解説より、飽和水溶液の温度を60℃から20℃に下げると、物質C(塩化ナトリウム)は結晶がほとんど析出しません。
塩化ナトリウムのように、温度を下げても溶解度があまり変化しない物質の再結晶を行う場合、水溶液を蒸発させて取り出す方法が用いられます。
大問5

問1
解答:光の反射
解説:
太陽や豆電球など自ら光を出すものを光源といいます。
光源が見えるのは、光源からの光が直接目に入るからで、光源以外のものが見えるのは、光源から出た光が物の表面で反射し、その光が目に入るからです。
図1や図2は、光があたかも一直線に進んでいるかのように見えますが、これはスリット(微少な穴)から出た光やレーザー光線を用いて光を一本線にして、分かりやすくしているだけです。
なお光は、さえぎるものがなければ同じ物質(空気やガラスなど)の中をまっすぐに進みます。これを光の直進といいます。
直進した光が、鏡などの面に当たって反射するとき、入射角=反射角が成り立ちます。
これを反射の法則といいます。
鏡などの面に垂直な線のことを法線といいます。
入射角、反射角、屈折角は、法線とのなす角度です。
問2
解答:
解説:
鏡やスクリーンなどに物体がうつって見えるものを、その物体の像といいます。
鏡の像は、鏡面について物体と線対称の位置にでき、実際にそこにはない像(虚像)を見ていることになります。
鏡に反射する光の経路の作図の手順は、以下の3ステップです。
①鏡面に対して光源(物)と対称な点(像)をとる。
②像と目を直線で結び、鏡面との交点をとる。
③光源と手順②でとった点を結ぶ。
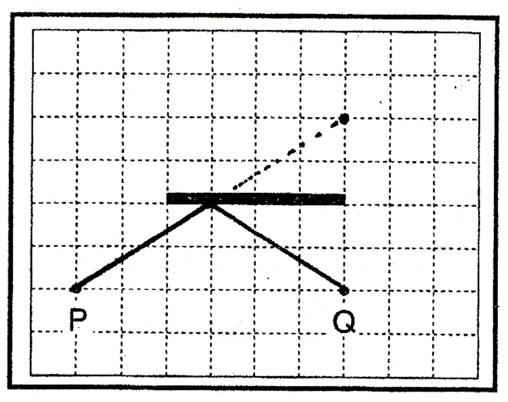
この問題では、Pが鏡に映ったQ(像、虚像)を見ています。
作図手順は、Qと鏡面について物体と線対称の位置にある点をとり、その点をPを結んだ線と鏡との交点が、Qから出た光が反射する点です。
問3
解答:ア、ウ
解説:
鏡にうつした物が見える範囲の作図には、以下の2通りの方法があります。
①鏡面について物体と線対称の位置に像を作図し、像と鏡の両端を通る2つの直線を作図する。
→2つの直線に挟まれた部分にいる人は、鏡にうつした物を見ることができる
②光源から鏡の両端に入射光線を引き、反射の法則から反射光線を作図する。
→反射光線に挟まれた部分にいる人は、鏡にうつした物を見ることができる
大問6
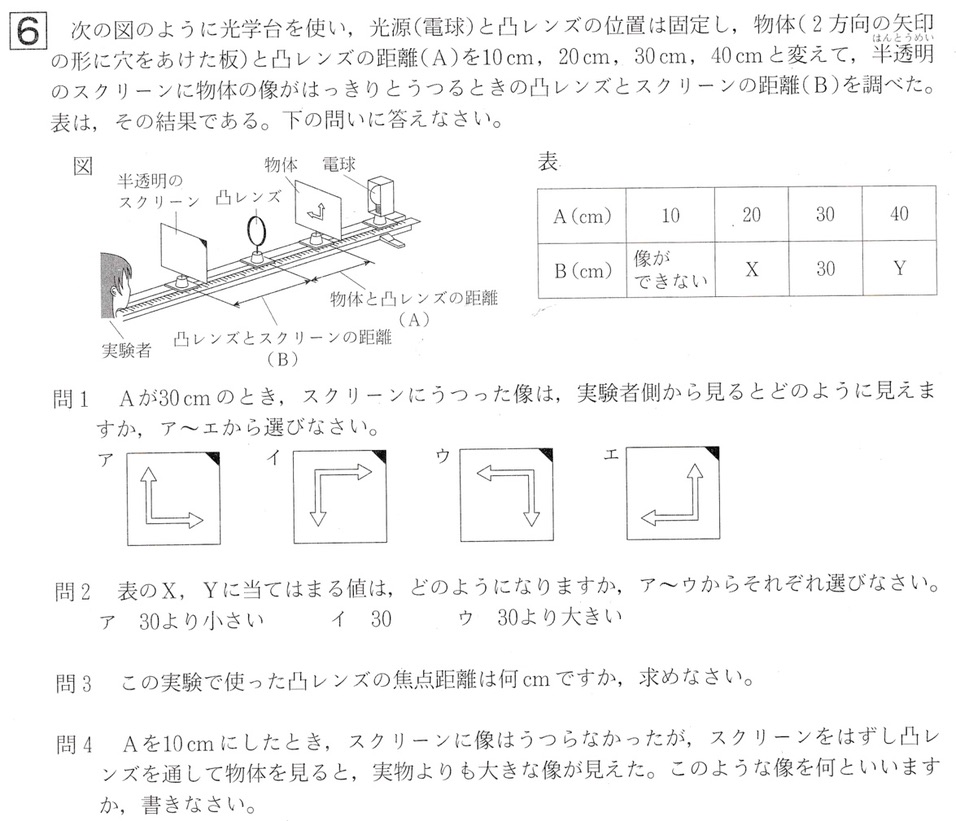
問1
解答:イ
解説:
凸レンズとは、ガラス中央部分がまわりよりも厚いレンズのことです。
凸レンズの軸(光軸)に平行に入射した光がレンズで屈折して1カ所に集まる点を焦点(英語でfocusより、Fと書くことが多い)といいます。
点とみなせる光源から四方に出る光のうち、凸レンズに入射する光の進み方は、以下の4つです。
①光軸に平行に進む光線は焦点を通る
②レンズの中心を通る光線はそのまま直進
③焦点を通った光線は光軸に平行に進む
④それ以外の光線は、レンズまで直進し、レンズで屈折後、光の集合点に向かう。
像の作図は、①〜③のうちの2本を作図することでできます。
凸レンズを通った光が集まってできる像を、実像といいます。
このときに見える像は、スクリーン側から見ると、物体とは上下・左右が逆向きに見えるため、倒立実像といいます。
物体側から見た場合は、上下のみが逆の像が見えます。
光源とレンズ間の距離をa、焦点距離をfとおくと、
①a>2f(焦点距離の2倍):実物より小さい倒立実像
②a=2f:実物と同じ大きさの倒立実像
③f<a<2f:実物より大きい倒立実像。a=1.5fのとき、倒立実像の大きさは実物の2倍
④a=f:像ができない
⑤a<f(焦点の内側):実物より大きい正立虚像
問題文の表を見ると、凸レンズからスクリーンまでの距離が30cmのとき、光源から凸レンズまでの距離を30cmにすると、スクリーンに実像がはっきりと映ります。
すなわち、像の作図手順に従って作図すると、凸レンズからスクリーンまでの距離と光源から凸レンズまでの距離が30cmになり、理論値と一致するするということです。
「②レンズの中心を通る光線はそのまま直進」する光線と、実物と実像とが作る二つの三角形は合同な三角形です(1組の辺とその両端の角がそれぞれ等しいから)。
ゆえに、実物と実像の大きさは等しく、光源は焦点距離の2倍の位置にあるので、凸レンズの焦点距離は30cm÷2=15cmです。
以上より、答えはイです。
なお、実験者が物体側から見た場合、上下のみ逆の像が見えるので、選択肢ウの像をスクリーンを通じて見ることができます。
問2
解答: X:ウ、Y:ア
解説:
・X
光源を凸レンズの焦点まで近づけていくと、倒立実像は遠ざかりながら大きくなります。
つまり、光源を凸レンズの焦点まで近づけていくと、凸レンズとスクリーンとの距離が長くなっていきます。
問1解説より、この凸レンズの焦点距離は15cmです。
A=20cmのとき、焦点距離(15cm)から焦点距離の2倍(30cm)の位置の間にあるので、実物より大きい倒立実像をスクリーンを通じて見ることができます。
実物と像の大きさが等しいのはA=30cmのときで、凸レンズとスクリーンとの距離も30cmです。
A=20cmのとき、実物より大きい倒立実像ができるで、凸レンズとスクリーンとの距離も30cmより長くなるため、X>30cmです。
・Y
A=40cmのとき、焦点距離の2倍(30cm)の位置より遠い位置にあるので、実物より小さい倒立実像をスクリーンを通じて見ることができます。
そのため、凸レンズとスクリーンとの距離は30cmより短くなるため、Y<30cmです。
問3
解答:15cm
解説:
問1解説参照。
問4
解答:虚像
解説:
凸レンズの焦点距離は15cmより、光源から凸レンズまでの距離が10cmでは、実物より大きい正立虚像(上下・左右が同じ)ができます。
光が集まらない像を虚像といい、スクリーンに映すことが出来ません。
物体を凸レンズの焦点の内側に置くと、凸レンズで屈折した光が目に入り、凸レンズを通して物体より大きな虚像が見えます(虫めがねの原理)。
大問7
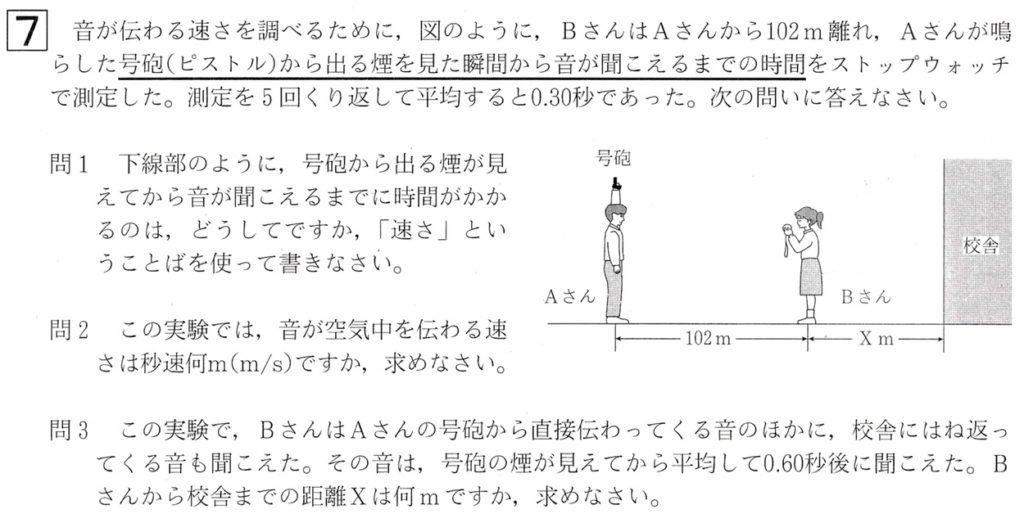
問1
解答:音が伝わる速さは、光の速さより遅いから。
解説:
音源が振動すると、その振動が波として広がり、空気などの音を伝える物質(媒質)に次々と伝わることで、音が伝わります。
空気の成分比率は、体積の割合で多い順から
窒素(約78%)、酸素(約21%)、アルゴン(約0.9%)、二酸化炭素(約0.04%)です。
このほか、ネオン、ヘリウムなども微量ですが含まれています。
これら空気を構成する原子や分子は質量[g]を持つ物体で、音波によって振動し、その振動が伝わっていくことで、音が伝わります。
同様に、水には水分子が、金属には銅原子や鉄原子などがあり、それらに音波の振動が伝わっていくことで、音が伝わります。
なお、音を伝える物質と音が伝わる速さは、気体<液体<固体の順に速くなります。
例えば、空気中での音が伝わる速さは約340m/s、水中での音が伝わる速さは約1500m/s、鉄の場合は約6000m/s、です。
100m離れた場所の場合、音が空気中を伝わって耳に届くまでにかかる時間は約0.3s(100m÷約340m/s)と、人が認識できる時間分かかります。
これに対して、光の速さは約3億m/sと非常に速いため、点灯してから目に届くまでの時間は無視できるほど小さい(0秒)とみなすことができます。
問2
解答:340m/s
解説:
問われている単位[m/s]を見ると、分子が距離[m]、分母が時間[s]です。
問題文を見ると、AさんとBさんの距離が102m、号砲がBさんに伝わる時間は平均して0.30秒(0.30s)なので、
音が空気中を伝わる速さ[m/s]は、
音が空気中を伝わる速さ[m/s]=102m/0.30s=1020/3m/s=340m/s
問3
解答:51m
解説:
号砲から発せられた音は、340m/sの速さで102+X+X(m)を0.60sで進むので、
102+X+X=340m/s×0.60s=34×6=204 ⇔ 2X=204 – 102=102 ⇔ X=102/2=51m
大問8
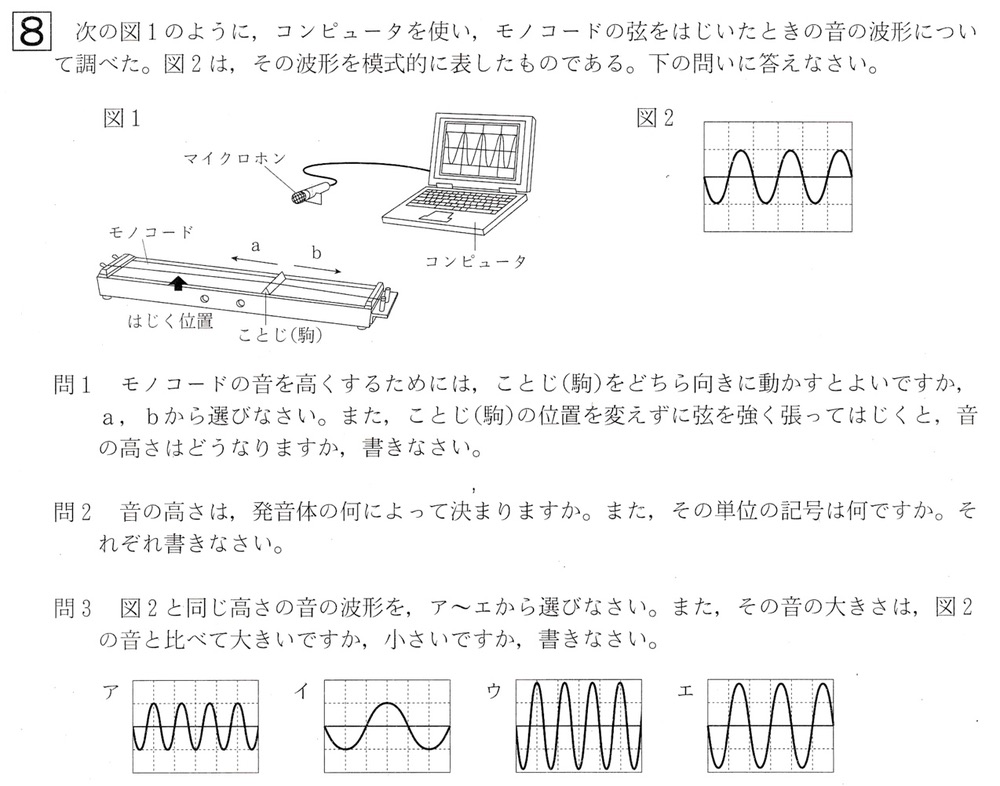
問1
解答: 向き:a、高さ:高くなる
解説:
おんさやモノコードの弦などを音源といいます。
おんさを叩いたり、モノコードを弾くなどすると、音源が振動し、その振動が波として広がり、空気などの音を伝える物質(媒質)に次々と伝わることで、音が伝わります。
このようにして広がる音の波を音波といいます。
音源が1回振動すると、音源のまわりの空気が押されたり引かれたりして密度が変化し、1組の山と谷ができます。
コンピューターを用いて波形を調べると、図2のような波形になります。
このとき、図2の中央を横切る線であるベースラインから、山または谷までの幅を振幅といいます。
振幅が大きいほど音が大きく、振幅が小さいほど音が小さいです。
図2の音波の波形を見ると、モノコードの振幅は1マスであることが分かります。
また、音波の波形の1つの山からとなりの山(1つの谷からとなりの谷)までが1つの波で、その長さを波長といいます。
図2の音波の波形では、波長は2マスであることが分かります。
図2の音波の波形は、左から右に、340m/sの速さで動いています。
1つの波が通過すると1回振動したといいます。
振動数とは、1秒間あたりに通過する波の数で、単位はHz(ヘルツ)です。
振動数が多いほど音が高く、振動数が小さいほど音が低いです。
例えば、図2の横の1目盛りが0.005秒のとき、1つの波の間隔は0.005秒×2=0.01秒より、0.01秒[s]で1回振動している(0.01秒で1つの波が通過している)ことから、
1秒間あたりに通過する波の数である振動数は、1/0.01s=100/1Hz=100Hz
となります。
モノコードとは、共鳴箱の上に1本または2本の弦を張って、音が出るようにした楽器です。
ことじを動かして弦の長さを変えたり、張りを変えたりして音の高さを変えることができます。
モノコードの弦と音の高さの関係は、以下の通りです。
・高い音
モノコードの弦の長さを短く、張り方を強く、太さを細くします。
・低い音
モノコードの弦の長さを長く、張り方を弱く、太さを太くします。
よって、モノコードの音を高くするには、弦を短くすればよいので、ことじをaの向きに動かすとよいです。
また、ことじのいちを変えずに弦を強く張ってはじくと、音の高さは高くなります。
問2
解答: 発音体の何:振動数、単位の記号:Hz
解説:
問1解説参照。
問3
解答: 波形:エ、大きさ:大きい
解説:
各選択肢の波形を見ます。
・ア
波長が1.5マスと図2の波長2マスより短いので、振動数が多く音が図2より高いです。振幅は変わらないので音の大きさは変わりません。
・イ
波長が4マスと図2の波長2マスより長いので、振動数が少なく音が図2より低いです。振幅は変わらないので音の大きさは変わりません。
・ウ
波長が1.5マスと図2の波長2マスより短いので、振動数が多く音が図2より高いです。また振幅が2マスと図2の1マスより大きいので図2より音が大きいです。
・エ
波長が2マスと図2の波長と同じなので、振動数が同じより音の高さは図2と同じです。また振幅が2マスと図2の1マスより大きいので図2より音が大きいです。
大問9
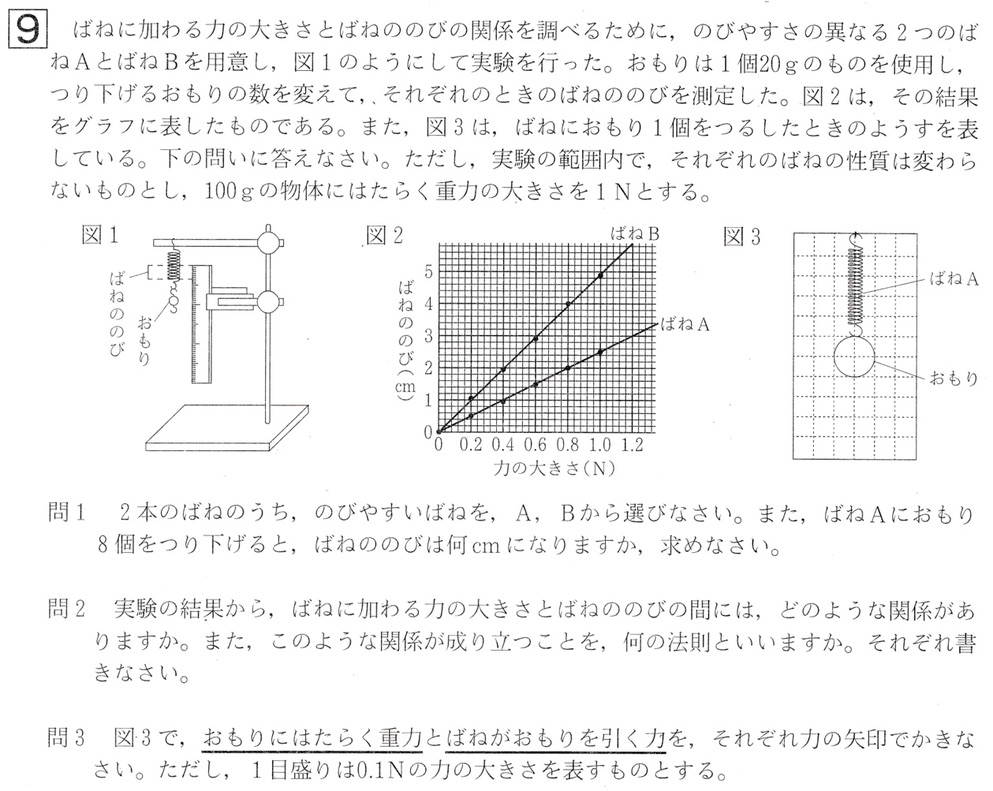
問1
解答: ばね:B、のび:4cm
解説:
変形した物体がもとの形に戻ろうとする力を弾性力といいます。
ばねは伸びたり縮んだりすると、自然長(元の長さ)に戻ろうとする力が働き、これをばねの弾性力といいます。
ばねにつるすおもりの質量を2倍、3倍・・・にすると、ばねの伸びも2倍、3倍・・・になり、ばねの弾性力も2倍、3倍・・・になります(伸びた分だけ弾性力が増していく)。
バネの伸び縮みした長さと、ばねの弾性力=ばねにかかる力の大きさは比例関係にあり、これをフックの法則といいます。
実際に図2をと、ばねAばねBともに、ばねを引く力の大きさが増すに従い、ばねの伸びは直線的に増加している、すなわち比例関係にあることが分かります。
このグラフの傾きをばね定数[N/m]といい、単位よりばね定数は、ばねを1m伸ばしたり縮めたりするのに必要な力の大きさとなります。
のびやすいばねとは、同じ質量[g](=同じ重さ[N])のおもりをつるしたときに、ばねの伸びが大きいばねのことです。
図2をみると、力の大きさが0.4Nのとき、ばねAは1cm、ばねBは2cmのびているので、ばねBのほうがのびやすいばねであるといえます。
また、ばねAにおもり8個をつり下げたとき、
おもり8個の合計の質量は160g(20g/個×8個)、
100gの物体にはたらく重力の大きさを1Nとしているので、おもり8個にはたらく重力の大きさは1.6N、
おもり8個がばねを引く力の大きさは、おもり8個にはたらく重力の大きさ1.6Nと等しいので、
ばねAにかかる力の大きさは1.6Nです。
ばねAは0.4Nの力がかかると1cm伸びるので、1cm/0.4N=1/0.4 cm/Nという関係が成り立ちます。
ゆえに、ばねAに1.6Nの力がかかると、ばねの伸びは、1/0.4 cm/N×1.6N=1.6/0.4 cm=16/4=4cm
問2
解答: 関係:比例、法則:フックの法則
解説:
問1解説参照。
問3
解答:

解説:
力は矢印で表します。
このとき、力の三要素である力の大きさを矢印の長さで、力の向きを矢印の指す向きで、力が加わる点である作用点を矢印の視点として、それぞれ表します。
力の矢印がのっている直線を、作用線といいます。
なお、地球上で質量100gの物体に働く重力(作用点は物体の中心)の大きさを1N(ニュートン)とすることが多いですが、
正確には、地球上で質量100gの物体に働く重力の大きさは0.98Nです。
・おもりにはたらく重力
重力は物体の中心から(鉛直)下向きに働きます。
問題文で、「100gの物体に働く重力の大きさを1Nとする」とあり、図3のおもり1個の質量は20gより、重力の大きさは、1N/100g×20g=1/5N=0.2Nです。
よって、力の大きさである矢印の長さは2目盛り、力の向きは鉛直下向き、作用点は物体の中心となります。
・ばねがおもりを引く力
おもりはばねによって、鉛直上向きの力を受けています。
このばねがおもりを引く力と、おもりにはたらく重力の大きさが釣り合うため、おもりは静止しています
ばねがおもりを引く力の、力の大きさである矢印の長さは2目盛り、力の向きは鉛直上向き、作用点はばねとおもりの接点です。
なお、おもりがばねを引く力は、おもりにはたらく重力と同じなので、力の大きさである矢印の長さは2目盛り、力の向きは鉛直下向き、作用点はばねとおもりの接点です。
図3ではばねが静止していますが、これは、おもりがばねを引く力と、天井がばねを引く力が釣り合っているためです。
ばねとおもりの接点で、おもりがばねを引く力(作用)と、ばねがおもりを引く力(反作用)がはたらきますが、
作用・反作用は同じ作用線上にあり、大きさが同じく向きが反対ですが、力が働く相手が異なるため、作用と反作用の2つの力は釣り合いとは無関係です。
大問10
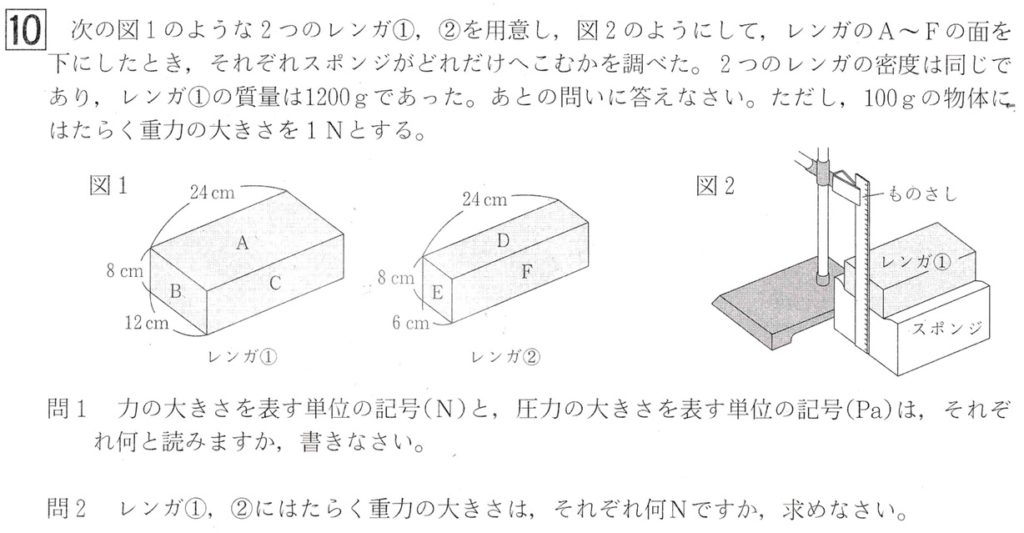

問1
解答: N:ニュートン、Pa:パスカル
解説:
解答の通りです。
力は物体に対して「点」ではたらきます。圧力は物体に対して「面」ではたらきます。
問2
解答: ①12N、②6N
解説:
重力は物体の中心から(鉛直)下向きに働きます。
・レンガ①
問題文で、「100gの物体に働く重力の大きさを1Nとする」とあり、図2のおもりの質量は1200gより、重力の大きさは、1N/100g×1200g=12Nです。
・レンガ②
レンガ②の質量[g]が分かれば、重力の大きさ[N]が分かります。
そのためにまず、レンガ①の密度[g/cm3]を求めます。
密度の単位[g/cm3]を見ると、分子が質量[g]で分母が体積[cm3]です。
レンガ①の質量[g]は、問題文より1200gです。
レンガ①の体積[cm3]は、図1より、8×12×24cm3です。
よって、レンガ①の密度[g/cm3]は、
レンガ①の密度[g/cm3]=1200g÷(8×12×24cm3)=100÷(8×24) g/cm3です。
レンガ①の密度[g/cm3]=レンガ②の密度[g/cm3](レンガ①と②は同じ材料でできている)、
レンガ②の体積は、図1より、8×6×24cm3です。
よって、レンガ②の質量[g]は、
100÷(8×24) g/cm3×8×6×24cm3=100×6g=600g、
レンガ②にはたらく重力の大きさは、
1N/100g×600g=6Nとなります。
「レンガ②の体積はレンガ①の体積の半分で、レンガ①と②の密度が同じだから、レンガ②にはたらく重力の大きさはレンガ①の半分の6Nである」
と解いてもよいです。
問3
解答: 面:B、圧力:1250Pa
解説:
圧力の単位[N/m2]に留意して以下のような比例式を立てます。
圧力A:圧力B=12N/12cm×24cm:12N/8cm×12cm=1/12×24:1/8×12=8×12:12×24=8:24=1:3=2:6
圧力B:圧力C==12N/8cm×12cm:12N/8cm×24cm=1/8×12:1/8×24=8×24:8×12=24:12=2:1=6:3より、
圧力A:圧力B:圧力C=2:6:3となり、圧力A<圧力C<圧力Bとなります。
ここで、レンガ①のA面、B面、C面をそれぞれ下にしてスポンジの上に置いたとき、いずれもレンガ①がスポンジに加える力[N]の大きさは12Nです。
レンガのA面、B面、C面の面積比は、
A面:B面:C面=12cm×24cm:8cm×12cm:8cm×24cm=24:8:8×2=3:1:2より、
B面<C面<A面となります。
これから、面が受ける垂直方向の力が同じ場合、
圧力比と面積比は逆比(大きさが逆になる)という関係が成り立ちます。
問4
解答:イ、オ、キ
解説:
圧力の単位[N/m2]に留意して、圧力aと圧力d、圧力bと圧力e、圧力cと圧力fの大小関係を調べます。
・圧力aと圧力d
面Aは面Dより面積が2倍なので、面積のみ見ると、面Aがスポンジに加える圧力の大きさは、面Dの1/2倍です。
面積のみ見ると、圧力a=1/2×圧力d、という関係になります。
しかし、レンガ①にはたら重力の大きさ12Nは、レンガ②の6Nの2倍です。
力の大きさのみ見ると、圧力a=2×圧力d、という関係になります。
よって、二つの式の係数をかけ合わせて、圧力a=圧力d、という関係が成り立ちます。
・圧力bと圧力e
面Bは面Eより面積が2倍なので、面積のみ見ると、面Bがスポンジに加える圧力の大きさは、面Eの1/2倍です。
面積のみ見ると、圧力b=1/2×圧力e、という関係になります。
しかし、レンガ①にはたら重力の大きさ12Nは、レンガ②の6Nの2倍です。
力の大きさのみ見ると、圧力b=2×圧力e、という関係になります。
よって、二つの式の係数をかけ合わせて、圧力b=圧力e、という関係が成り立ちます。
・圧力cと圧力f
面Cは面Fと面積が等しいので、面積のみ見ると、面cがスポンジに加える圧力の大きさは、面fと同じです。
面積のみ見ると、圧力c=圧力f、という関係になります。
しかし、レンガ①にはたら重力の大きさ12Nは、レンガ②の6Nの2倍です。
力の大きさのみ見ると、圧力c=2×圧力f、という関係になります。
よって、二つの式の係数をかけ合わせて、圧力c=2×圧力f、という関係が成り立ちます。
大問11

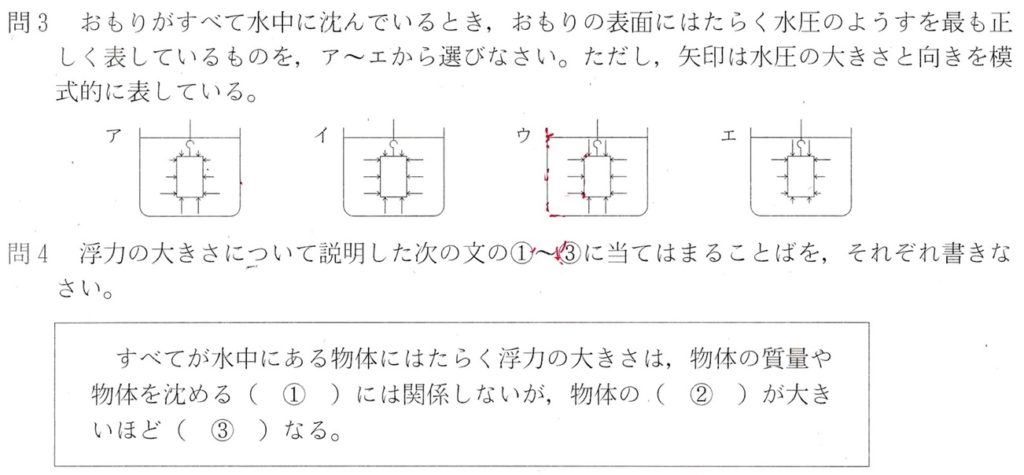
問1
解答:0.70N
解説:
ばねばかりを用いて、物体の重さを水中ではかると、物体は水から鉛直上向きの力を受け、空気中ではかるよりも軽くなる。
この力を浮力といいます。
物体は水中では、上面と下面、左右の面それぞれから水の圧力である水圧を受けます。
水圧は物体が深く沈むほど、大きくなります。
左右の面が受ける水圧の大きさは等しいので、互いに打ち消し合います。
しかし、上面と下面では、下面にかかる水圧の大きさ(鉛直上向き)が上面にかかる水圧の大きさ(鉛直下向き)より大きいため、その差が浮力となります。
また、浮力[N]とは物体が押しのけた流体の重さ[N]ということができ、これをアルキメデスの原理といいます。
仮に、水の密度を1.0g/cm3(4℃の水)とします。
物体の体積は50cm3より、物体をこの水に完全に沈めた場合、物体が押しのけた水の体積は50cm3、50cm3の水の質量[g]は、1.0g/cm3×50cm3=50gです。
100gの物体にはたらく重力の大きさを1Nと仮定すると、50cm3の水の重さ[N]は、1N/100g×50g=1/2N=0.5Nとなるので、
物体に働く浮力の大きさは0.5Nとなります。
物体に働く重力の大きさは、場所によらず一定です。
力は物体の中心から(鉛直)下向きに働きます。
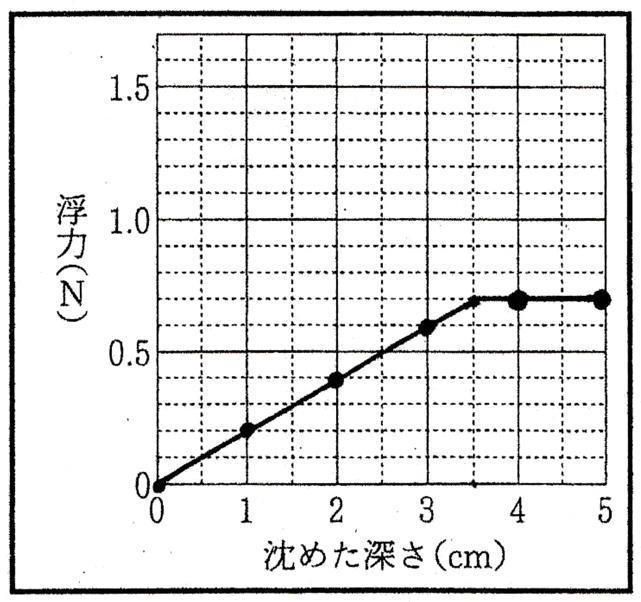
表を見ると、おもりを沈めた深さが0cm、すなわち物体を水に沈めずばねばかりでつるしただけの状態のときのばねばかりの値は1.55Nより、物体に働く重力の大きさは1.55Nです。
アルキメデスの原理より、物体に働く浮力の大きさは、物体の体積に依存します。
図1を見ると、おもりの高さは3.5cmなので、おもりを沈めた深さが3.5cm以上になると、おもりにはたらく浮力の大きさは変化しなくなります。
表より、おもりを沈めた深さが4cmのとき、ばねばかりの値が0.85Nより、おもりにはたらく浮力の大きさは、
1.55N – 0.85N=0.70N
※表では1.55N と、少数第二位まで表示されているので、少数第二位まで答えます。
問2
解答:
解説:
問1解説参照。
問3
解答:ア
解説:
物体は水中では、上面と下面、左右の面それぞれから水の圧力である水圧を受けます。
水圧は物体が深く沈むほど、大きくなります。
左右の面が受ける水圧の大きさは等しいので、互いに打ち消し合います。
しかし、上面と下面では、下面にかかる水圧の大きさ(鉛直上向き)が上面にかかる水圧の大きさ(鉛直下向き)より大きいため、その差が浮力となります。
問4
解答: ①深さ、②体積、③大きく
解説:
浮力[N]とは物体が押しのけた流体の重さ[N]ということができ、これをアルキメデスの原理といい、物体に働く浮力の大きさは、物体の体積に依存します。
すべてが水中にある物体にはたらく浮力の大きさは、体積が一定ならば、物体の質量や沈める深さによらず一定です。
しかし物体の体積が大きくなると、物体が押しのけた水の体積[cm3]が増加するので、押しのけられた水の質量[g]も増加し、押しのけられた水の重さ[N]も増加するため、
物体にはたらく浮力の大きさは大きくなります。