指導経験20年以上のプロ家庭教師。北海道の高校受験に特化。勉強がとても苦手な子の指導が得意です。
＞＞ブログ記事一覧（目次）
＞＞5教科・偏差値別オススメ問題集一覧
第1問
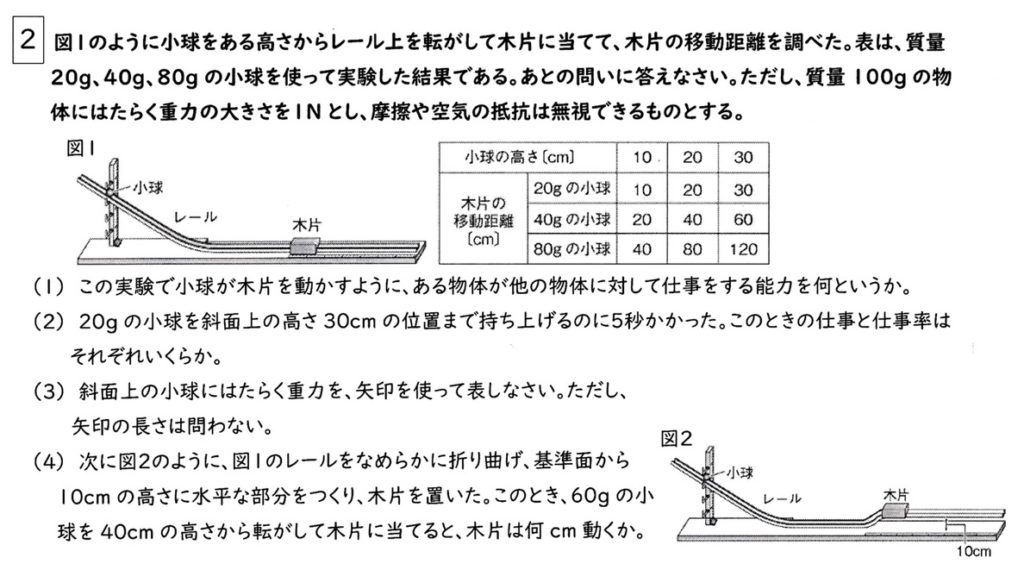
（1）
答：エネルギー（解説略）
（2）
仕事[J]＝0.2N×0.3m＝(2/10)×(3/10)＝6/100＝0.06J
仕事量[J/s]＝0.06J/5s＝(6/100)×(1/5)＝1.2/100＝0.012J/s
（3）
重力とは、地球の中心が及ぼす鉛直下向きの力で、場所によらず向きが同じです。
よって、小球の中心を作用点とし、鉛直下向きに矢印を書いて終わりです。
なお、高校物理では、重力は、2つの質量を持つ物体同士が及ぼし合う力である万有引力の一種だと習います。
（4）
小球と木片の位置との差は30cmなので、表の3列目を見ます。
位置エネルギー＝重力×高さ、より、木片の移動距離は小球の質量と高さに比例します。
ゆえに、20gの1.5倍の質量である30gのとき、木片の移動距離は、30cm×1.5＝＝3×15＝45cm。
第2問（難）
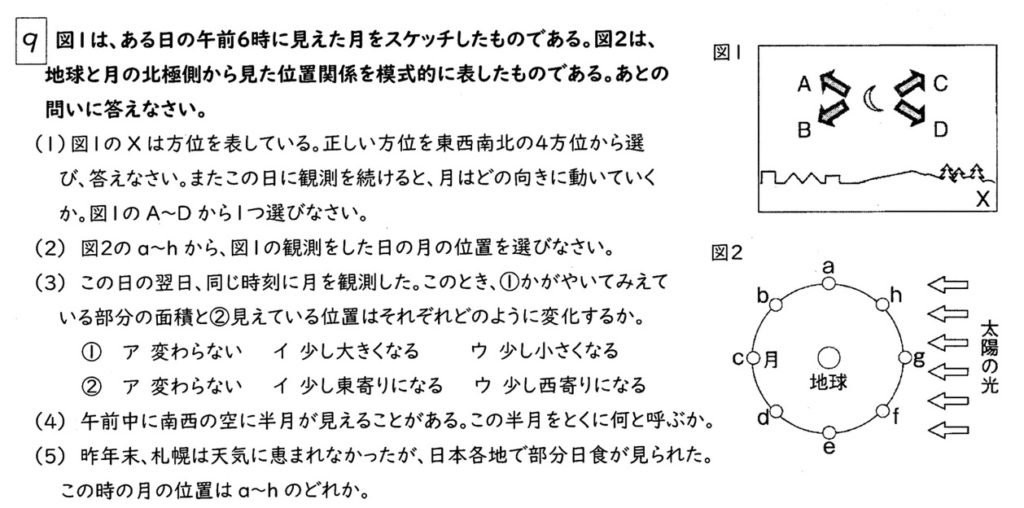
半端な知識では対応できない良問です。
この中学の先生の作問能力の高さに脱帽しました。
（1）＜難＞
天体上で考えます。
午前6時は明け方です。
月は30日周期で、新月から右から満ちて満月になり、満月から右から欠けて新月になります。
月は地球の周りを反時計回り（西から東）に公転する衛星で、図1の月は新月に近いことから、明け方南東の空に月が見えます。
ゆえに、図1のXは南の方角です。
地球は西から東（反時計回り）に1日360°、1時間に15°自転しているため、1日でみると、星や太陽などの恒星は、1時間に15°東から西に動いて見えます。
月を地球上で観察すると、月の公転周期である満ち欠けの周期は29.5日と地球の自転周期1日と比べて回転速度が遅いので、
1日でみると、月は東から西に動いて見えます。見かけの動きの速度は1時間に15°より低いです。
ゆえに、月が図1の南東の位置にあるとき、南の方角のXの方向（C）へ動いて見えます。
（2）
図1の月は新月の手前であることから、fの位置であると推測できます。
（1）より、明け方南東の空に月が見えたことから、fの位置で正しいことが分かります。
（3）＜難＞
月は地球の周りを反時計回り（西から東）に公転する衛星です。
月を地球上で観察すると、月の公転周期である満ち欠けの周期は29.5日から、同一時刻に月を観察すると、月は1日あたり約12°（360°÷29.5日≒12°）西から東へ移動して見えます。
月は30日周期で、新月から右から満ちて満月になり、満月から右から欠けて新月になります。
以上から、図1の翌日の同一時刻に月を観察すると、東に約12°移動して見え（②：ウ、図1ではBの方向に移動して見える）、月は図1より少し欠けて見えます（①：ア）。
（4）＜やや難＞
図2を用いて調べます。
地球は西から東（反時計回り）に自転します。
月は地球の周りを反時計回り（西から東）に公転する衛星です。
月は30日周期で、新月から右から満ちて満月になり、満月から右から欠けて新月になります。
明け方から正午までの位置が午前中で、この位置で南西の空に見えるのはeです。
月が地球を挟んで太陽と反対方向に位置したcが満月なので、eは下弦の月です。
（5）
月は地球の周りを反時計回り（西から東）に公転する衛星です。
月は30日周期で、新月から右から満ちて満月になり、満月から右から欠けて新月になります。
日食とは太陽が月に遮られた状態なので、月が新月の位置（g）のときに起こります。
スポンサーリンク
第3問
（1）
答：恒星（解説略）
（2）
我々は、冬の季節の星座であるオリオン座のリゲルから860年前に放たれた光を見ています。
（3）
地球は西から東（反時計回り）に自転しているため、1日でみると、星は東から西に動いて見えます。これを星の日周運動といいます。
地球は1時間に15°自転しますが、星は公転をしない恒星なので、星も1時間に15°動いて見えます。
1日単位で見ると、星は1日1°の速度で、東から西に動いて見えます。
これを星の日周運動といいます。
また、地球は西から東（反時計回り）に1年360°＝1ヶ月30°＝1日1°の速度で公転しているため、同一時刻に星を観察すると、1日1°ずつ東から西に動いて見えます。
これを星の年周運動といいます。
この問題では、星の日周運動のみ考えます。
図1の南の方角の左側が東、右側が西で、Aと南とイのなす角度は約60°と読めるので、Aから4時間前の19時にイが観測できたと考えられます。
（4）
北の空で観察できる北極星は2等星で、あまり目立たないため、北斗七星やカシオペア座を目印にして見つけます。
図2は北の空で、Rは北極星です。
北極星は地軸の延長線上にあるため、ほとんど動きません（星は公転をしない恒星なので、動いて見えないというのが正確です）
（5）
星の日周運動・年周運動において、北の空で星を観察すると、反時計回りに動いて見えます。
星の日周運動の見かけの動きの速度は、1日360°＝1時間に15°です。
星の年周運動の見かけの動きの速度は、1年360°＝1ヶ月30°＝1日1°です。
Aの位置から3ヶ月後の21時に、星は30°×3＝90°反時計回りに移動して、ケの位置に見えます。
そこから2時間前の19時に、星は15°×2＝30°時計回りに移動して、コの位置に見えます。
（6）
北半球と南半球で東西南北の方角は同じなので、オリオン座は南東に見えます。
しかし、北半球では北の空を背に南の空から星や太陽を見ているのに対し、南半球では南の空を背に北の空から星や太陽を見ていることになります。
北半球で19時にオリオン座が南東の空に見えたとき、図1ではアの位置に見え、時間とともに左（東）から右（西）に動いて見えます。
南半球で19時にオリオン座が南東の空に見えたとき、図1の「南」を北に置き換えて、時間とともに右（東）から左（西）に動いて見えます。
また北半球と南半球とで、オリオン座の形は上下逆の関係になります。
※
知らなかったので、ネットを使って自分なりに調べました。
参考サイト）
第4問（難）
（1）
地球は西から東（反時計回り）に自転しているため、1日でみると、太陽は東から西に動いて見えます。これを太陽の日周運動といいます。
透明半球でBを東、Dを西、Aを南、Cを北とおいて太陽の動きをとらえると、太陽は南に傾いて、東から西に動いていることが分かります。
AとCを結んだ半円形の線を天の子午線といい、太陽が天の子午線にきたとき、太陽が南中したといいます。
このとき、中心から太陽を見上げた角度を南中高度、太陽が南中した時刻を南中時刻といいます。
天体上で考えて、地球は公転面と垂直な線に対して地軸を23.4°傾けながら反時計回りに公転しています。
地球が地軸の北極側を太陽と反対方向に傾けているとき、北半球の同一地点では、南中高度が低く、昼が短く夜が長くなり、地表面に降り注ぐ太陽からの光エネルギーが低いため、気温が低く冬になります（a）。
地球が地軸の北極側を太陽に傾けているとき、北半球の同一地点では、南中高度が高く、昼が長く夜が短くなり、地表面に降り注ぐ太陽からの光エネルギーが高いため、気温が高く夏になります（c）。
これより、季節の変化が起こっていることが分かります。
（2）
透明半球で太陽の動きをとらえるとき、サインペンの先の影が中心O（①〜③）にくるような位置を探して印をつけます。
（3）
答：南中高度（解説略）
（4）＜難＞
天体上で考えて、北半球にて同じ日に同一経度で太陽を観察すると、高緯度になると南中高度が低くなります。
よって札幌の方が東京より南中高度が低いので、影の長さは札幌の方が大きくなります（ア）
天体上で考えて、地球は公転面と垂直な線に対して地軸を23.4°傾けながら反時計回りに公転することで、同じ場所では南中高度が変化します。
具体的には、夏は90° – 緯度＋23.4°、春・秋は90° – 緯度、冬は90° – 緯度 – 23.4°、です。
天体上または天球上で考えて、夏は南中高度が高いため、昼が長く夜が短くなります。冬は南中高度が低いため、昼が短く夜が長くなります。
しかし、北半球にて同じ日に同一経度で太陽を観察すると、高緯度になると南中高度が低くなりますが、昼が長く、日の出が早くなります。
この事実は天体上で考えることで、はっきりと分かります。
南中高度が高いほど昼が長い、というわけではないということです。
（5）＜難＞
テープ3cmが1時間に相当するので、8.5cmは、(1/3 h/cm)×8.5cm＝8.5/3h＝2h＋2.5/3h＝2h＋2.5/3×60min＝2＋2.5×20＝2h＋50min、に相当します。
9時の2時間50分前は、6時10分です。
（6）
解答例：地球が公転面と垂直な線に対して地軸を23.4°傾けながら反時計回りに公転しているため（（1）解説参照）